Преобразование Анскомба

Стандартное отклонение преобразованной случайной величины Пуассона как функция среднего значения $m$.

В статистике , преобразование Анскомба названное в честь Фрэнсиса Анскомба , представляет собой преобразование, стабилизирующее дисперсию , которое преобразует случайную величину с распределением Пуассона в величину с примерно стандартным распределением Гаусса . Преобразование Анскомба широко используется в визуализации с ограниченным количеством фотонов (астрономия, рентгеновские лучи), где изображения естественным образом подчиняются закону Пуассона. Преобразование Анскомба обычно используется для предварительной обработки данных, чтобы сделать стандартное отклонение примерно постоянным. Затем алгоритмы шумоподавления , разработанные для аддитивного белого гауссовского шума используются ; окончательная оценка затем получается путем применения обратного преобразования Анскомба к очищенным от шума данным.

Анимированная трансформация Анскомба. Здесь $\mu$ является средним значением распределения Пуассона, преобразованного Анскомбом, нормализованного путем вычитания на $2{\sqrt {m+{\tfrac {3}{8}}}}-{\tfrac {1}{4\,m^{1/2}}}$, и $\sigma$ – его стандартное отклонение (оценено эмпирически). Мы замечаем, что $m^{3/2}\mu$ и $m^{2}(\sigma -1)$ остается примерно в пределах $[0,10]$ за этот период, что дает эмпирическую поддержку $\mu =O(m^{-3/2}),\sigma =1+O(m^{-2})$

Определение

Для распределения Пуассона среднее значение $m$ и дисперсия $v$ не являются независимыми: $m=v$. Преобразование Анскомба

$A:x\mapsto 2{\sqrt {x+{\tfrac {3}{8}}}}\,$

направлен на преобразование данных так, чтобы дисперсия устанавливалась примерно 1 для достаточно большого среднего значения; для среднего нуля дисперсия по-прежнему равна нулю.

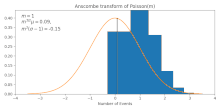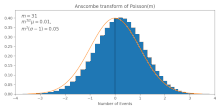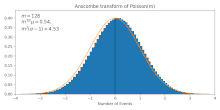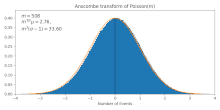
Он преобразует данные Пуассона $x$ (со средним $m$) до приблизительно гауссовых данных среднего $2{\sqrt {m+{\tfrac {3}{8}}}}-{\tfrac {1}{4\,m^{1/2}}}+O\left({\tfrac {1}{m^{3/2}}}\right)$ и стандартное отклонение $1+O\left({\tfrac {1}{m^{2}}}\right)$. Это приближение становится более точным для больших $m$, как это также видно на рисунке.

Для преобразованной переменной вида $2{\sqrt {x+c}}$, выражение для дисперсии имеет дополнительный член ${\frac {{\tfrac {3}{8}}-c}{m}}$; оно сводится к нулю при $c={\tfrac {3}{8}}$, и именно поэтому было выбрано это значение.

Инверсия

Когда преобразование Анскомба используется для шумоподавления (т. е. когда цель состоит в том, чтобы получить из $x$ оценка $m$), также необходимо его обратное преобразованиечтобы вернуть данные со стабилизацией дисперсии и шумоподавлением $y$ в исходный диапазон.Применение алгебраического обратного

$A^{-1}:y\mapsto \left({\frac {y}{2}}\right)^{2}-{\frac {3}{8}}$

обычно вносит нежелательное смещение в оценку среднего значения $m$, поскольку прямой квадратный кореньпреобразование не является линейным . Иногда используют асимптотически несмещенную обратную

$y\mapsto \left({\frac {y}{2}}\right)^{2}-{\frac {1}{8}}$

смягчает проблему предвзятости, но это не относится к визуализации с ограниченным количеством фотонов, для которойточное несмещенное обратное, заданное неявным отображением

$\operatorname {E} \left[2{\sqrt {x+{\tfrac {3}{8}}}}\mid m\right]=2\sum _{x=0}^{+\infty }\left({\sqrt {x+{\tfrac {3}{8}}}}\cdot {\frac {m^{x}e^{-m}}{x!}}\right)\mapsto m$

следует использовать. Аппроксимация в замкнутой форме равна этого точного несмещенного обратного значения

$y\mapsto {\frac {1}{4}}y^{2}-{\frac {1}{8}}+{\frac {1}{4}}{\sqrt {\frac {3}{2}}}y^{-1}-{\frac {11}{8}}y^{-2}+{\frac {5}{8}}{\sqrt {\frac {3}{2}}}y^{-3}.$

Альтернативы

Существует много других возможных преобразований, стабилизирующих дисперсию, для распределения Пуассона. Отчет Бар-Лева и Эниса семейство таких преобразований, включающее преобразование Анскомба. Еще одним членом семейства является преобразование Фримена-Тьюки.

$A:x\mapsto {\sqrt {x+1}}+{\sqrt {x}}.\,$

Упрощенное преобразование, полученное как примитив обратного стандартного отклонения данных :

$A:x\mapsto 2{\sqrt {x}}\,$

который, хотя и не так хорош в стабилизации дисперсии, имеет то преимущество, что его легче понять.Действительно, из дельта-метода ,

$V[2{\sqrt {x}}]\approx \left({\frac {d(2{\sqrt {m}})}{dm}}\right)^{2}V[x]=\left({\frac {1}{\sqrt {m}}}\right)^{2}m=1$.

Обобщение

Хотя преобразование Анскомба подходит для чистых данных Пуассона, во многих приложениях данные также представляют собой аддитивную гауссову составляющую. Эти случаи рассматриваются с помощью обобщенного преобразования Анскомба. и его асимптотически несмещенные или точные несмещенные обратные.

См. также

• Преобразование, стабилизирующее дисперсию
• Преобразование Бокса – Кокса

Дальнейшее чтение

• Старк, Ж.-Л.; Мурта, Ф. (2001), «Астрономические изображения и обработка сигналов: взгляд на шум, информацию и масштаб», журнал Signal Processing Magazine, IEEE , vol. 18, нет. 2, стр. 30–40, Bibcode : 2001ISPM...18...30S , doi : 10.1109/79.916319 , S2CID   13210703