Миметическая интерполяция

В математике миметическая интерполяция — это метод интерполяции дифференциальных форм . В отличие от других методов интерполяции, которые оценивают поле в определенном месте по его значениям в соседних точках, миметическая интерполяция оценивает поле. $k$ поля -форма задана проекцией на соседние элементы сетки. Элементами сетки могут быть точки сетки, а также края или грани ячеек, в зависимости от $k=0,1,2,\cdots$.

Миметическая интерполяция особенно актуальна в контексте векторных и псевдовекторных полей, поскольку метод сохраняет линейные интегралы и потоки соответственно.

Интерполяция интегрированных форм

Позволять $\omega ^{k}$ быть дифференциалом $k$-form, то миметическая интерполяция представляет собой линейную комбинацию

$${\bar {\omega }}^{k}=\sum _{i}\left(\int _{M_{i}}\omega ^{k}\right)\phi _{i}^{k}$$

где ${\bar {\omega }}^{k}$ это интерполяция $\omega ^{k}$, а коэффициенты $\int _{M_{i}}\omega ^{k}$ представляют напряженность поля на элементе сетки $M_{i}$. В зависимости от $k$, $M_{i}$ может быть узлом ( $k=0$), край ячейки ( $k=1$), грань ячейки ( $k=2$) или объём ячейки ( $k=3$). В приведенном выше $\phi _{i}^{k}$ являются интерполяционными $k$-формы, в центре которых $M_{i}$ и распадаться вдали от $M_{i}$ аналогично функциям палатки . Примеры $\phi _{i}^{k}$ формы Уитни для симплициальных сеток в $n$ размеры.

Важным преимуществом миметической интерполяции перед другими методами интерполяции является то, что напряженность поля $\int _{M_{i}}\omega ^{k}$ являются скалярами и поэтому инвариантны для системы координат.

Интерполирующие формы

Во многих случаях желательно использовать интерполяционные формы $\phi _{i}^{k}$ подобрать напряженность поля на отдельных элементах сетки без вмешательства других $\phi _{j}^{k}$. Это позволяет назначать значения полей конкретным элементам сетки, которые затем можно интерполировать между ними. Распространенным случаем является линейная интерполяция , для которой интерполирующие функции ( $0$-forms) равны нулю на всех узлах, кроме одного, где интерполирующая функция равна единице. Аналогичная конструкция может быть применена к миметической интерполяции.

$\int _{M_{j}}\phi _{i}^{k}=\delta _{ij}.$

То есть интеграл $\phi _{i}^{k}$ равно нулю для всех элементов ячейки, кроме $M_{i}$ где интеграл возвращает единицу. Для $k=0$ это составляет $\phi _{i}^{0}(x_{j})=\delta _{ij}$ где $x_{j}$ является точкой сетки. Для $k=1$ интеграл идет по ребрам и, следовательно, интеграл $\int _{M_{j}}\phi _{i}^{1}$ нулевое ожидание на краю $M_{i}$. Для $k=2$ интеграл ведется по граням и для $k=3$ над объемами клеток.

Свойства сохранения

Миметическая интерполяция учитывает свойства дифференциальных форм. В частности, теорема Стокса

$$\int _{M}{\overline {d\omega ^{k}}}=\int _{\partial M}{\bar {\omega }}^{k}$$

доволен ${\overline {d\omega ^{k}}}$ обозначающий интерполяцию $d\omega ^{k}$. Здесь, $d$ — внешняя производная , $M$ любое многообразие размерности $k$ и $\partial M$ является границей $M$. Это придает миметической интерполяции свойства сохранения, которые обычно не свойственны другим методам интерполяции.

Коммутативность между оператором интерполяции и внешней производной

Комплекс Де Рама . Вверху: пространства дифференциальных форм в трех измерениях. Внизу: соответствующие дискретизированные версии дифференциальных форм, полученные после интерполяции. Условие коммутативности гарантирует, что штриховые и штрихпунктирные пути дают одинаковый результат для каждой ячейки де Рама.

Чтобы быть миметичной, интерполяция должна удовлетворять

$$I_{k+1}(d\omega ^{k})=d(I_{k}\omega ^{k})$$

где $I_{k}$ является оператором интерполяции $k$-форма, т.е. ${\bar {\omega }}^{k}=I_{k}\omega ^{k}$. Другими словами, операторы интерполяции и внешние производные коммутируют. Обратите внимание, что для каждого типа формы требуются разные методы интерполяции ( $k=0,1,\cdots$), $I_{k+1}\neq I_{k}$. Приведенное выше уравнение — это все, что необходимо для удовлетворения теоремы Стокса для интерполированной формы

$$\int _{M}{\overline {d\omega ^{k}}}=\int _{M}I_{k+1}(d\omega ^{k})=\int _{M}d(I_{k}\omega ^{k})=\int _{\partial M}I_{k}\omega ^{k}=\int _{\partial M}{\bar {\omega }}^{k}.$$

Другие свойства исчисления вытекают из коммутативности между интерполяцией и $d$. Например, $d^{2}\omega =0$,

$$\int _{M}I_{k+2}(d^{2}\omega ^{k})=\int _{M}d(I_{k+1}d\omega ^{k})=\int _{\partial M}I_{k+1}d\omega ^{k}=\int _{\partial M}d(I_{k}\omega ^{k})=0.$$

Последний шаг дает ноль, так как $\int _{\partial M}d(\cdot )=0$ при интегрировании по границе $\partial M$.

Проекция

Интерполированный ${\bar {\omega }}^{k}$ часто проецируется на цель, $k$-мерные ориентированные многообразия $T$, $$\int _{T}{\bar {\omega }}^{k}=\sum _{i}\left(\int _{M_{i}}\omega ^{k}\right)\left(\int _{T}\phi _{i}^{k}\right).$$Для $k=0$ цель – это точка, т.к. $k=1$ это линия, потому что $k=2$ площадь и т. д.

Приложения

Многие физические поля можно представить в виде $k$-формы. При дискретизации полей при численном моделировании каждый тип $k$-форма часто приобретает собственную шаткость в соответствии с требованиями числовой устойчивости, например необходимостью предотвращения неустойчивости шахматной доски. Это привело к разработке внешнего конечного элемента. и методы дискретного внешнего исчисления , оба из которых основаны на дискретизации поля, совместимой с типом поля.

В таблице ниже перечислены некоторые примеры физических полей, их тип, соответствующая им форма и метод интерполяции, а также программное обеспечение, которое можно использовать для интерполяции, переназначения или изменения сетки поля:

пример поля	тип поля	эквивалент в k-форме	цель	ошеломляющий	Метод интерполяции (пример)	пример программного обеспечения
температура	скаляр	0-форма	точка	узловой	билинейный, трилинейный	ESMF
электрическое поле	вектор	1-форма	линия	край	край	КАК
магнитное поле	псевдовектор	2-форма	область	лицо	лицо	КАК
плотность	псевдоскалярный	3-форма	объем	клетка	взвешенный по площади, консервативный	СКРИП, ESMF

Пример

Индексация узлов и ребер четырехугольной ячейки, как показано в примере. Края выбраны так, чтобы указывать в восточном и северном направлениях.

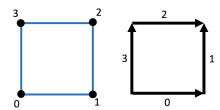
Рассмотрим четырехугольные ячейки в двух измерениях с индексированными узлами. $i=0,1,2,3$ в направлении против часовой стрелки. Далее, пусть $\xi _{1}$ и $\xi _{2}$ — параметрические координаты каждой ячейки ( $0\leq \xi _{1},\xi _{2}\leq 1$). Затем $${\begin{aligned}\phi _{0}^{0}&=(1-\xi _{1})(1-\xi _{2})\\[0.6ex]\phi _{1}^{0}&=\xi _{1}(1-\xi _{2})\\[0.6ex]\phi _{2}^{0}&=\xi _{1}\xi _{2}\\[0.6ex]\phi _{3}^{0}&=(1-\xi _{1})\xi _{2}.\end{aligned}}$$

являются билинейными интерполяционными формами $I_{0}$ в единичном квадрате ( $\xi _{1},\xi _{2}$). Соответствующий $I_{1}$ интерполяционные формы по краям являются

$${\begin{aligned}\phi _{0}^{1}&=(1-\xi _{2})d\xi _{1}\\[0.6ex]\phi _{1}^{1}&=\xi _{1}d\xi _{2}\\[0.6ex]\phi _{2}^{1}&=\xi _{2}d\xi _{1}\\[0.6ex]\phi _{3}^{1}&=(1-\xi _{1})d\xi _{2},\end{aligned}}$$

Четыре векторных поля, двойственные четырем реберным интерполирующим формам, прикреплены к четырехугольной ячейке. Векторные поля наиболее сильны на опорном крае и уменьшаются до нуля к противоположному краю. Обратите внимание, как векторные поля изгибаются, обеспечивая перпендикулярность по отношению к ребрам, примыкающим к опорному ребру.

где мы предполагали, что края будут индексироваться против часовой стрелки и с краями, указывающими на восток и север. В самом низком порядке существует только одна интерполирующая форма для $I_{2}$,

$$\phi _{0}^{2}=d\xi _{1}\wedge d\xi _{2},$$

где $\wedge$ это клиновое произведение .

Мы можем убедиться, что приведенные выше интерполяционные формы удовлетворяют миметическим условиям $I_{1}d\omega ^{0}=d(I_{0}\omega ^{0})$ и $d(I_{1}\omega ^{1})=I_{2}d\omega ^{1}$. Возьмем, к примеру,

$${\begin{aligned}d(I_{0}\omega ^{0})&=d\left(f_{0}(1-\xi _{1})(1-\xi _{2})+f_{1}\xi _{1}(1-\xi _{2})+f_{2}\xi _{1}\xi _{2}+f_{3}(1-\xi _{1})\xi _{2}\right)\\[0.6ex]&=(f_{1}-f_{0})(1-\xi _{2})d\xi _{1}+(f_{2}-f_{1})\xi _{1}d\xi _{2}+(f_{2}-f_{3})\xi _{2}d\xi _{1}+(f_{3}-f_{0})(1-\xi _{1})d\xi _{2}\\[0.6ex]&=(f_{1}-f_{0})\phi _{0}^{1}+(f_{2}-f_{1})\phi _{1}^{1}+(f_{2}-f_{3})\phi _{2}^{1}+(f_{3}-f_{0})\phi _{3}^{1}\\[0.6ex]&=I_{1}d\omega ^{0}\end{aligned}}$$где $f_{0}=\omega ^{0}(0,0)$, $f_{1}=\omega ^{0}(1,0)$, $f_{2}=\omega ^{0}(1,1)$ и $f_{3}=\omega ^{0}(0,1)$ — это значения полей, вычисляемые в углах четырехугольника в единичном квадратном пространстве. Аналогично, мы имеем

$${\begin{aligned}d(I_{1}\omega ^{1})&=d(g_{0}(1-\xi _{2})d\xi _{1}+g_{1}\xi _{1}d\xi _{2}+g_{2}\xi _{2}d\xi _{1}+g_{3}(1-\xi _{1})d\xi _{2})\\[0.6ex]&=(g_{0}+g_{1}-g_{2}-g_{3})d\xi _{1}\wedge d\xi _{2}\\[0.6ex]&=I_{2}d\omega ^{1}\end{aligned}}$$с $g_{i}=\int _{M_{i}}\omega ^{1}$, $i\in \{0,1,2,3\}$, являясь 1-формой $\omega ^{1}$проецируется на край $i$. Обратите внимание, что $g_{i}$ также известен как откат . Если $F:\mathbb {R} \rightarrow \mathbb {R} ^{2}$ это карта, которая параметризует край $i$, $x=F_{i}(t)$, $0\leq t\leq 1$, затем $g_{i}=\int {F_{i}}^{*}\omega ^{1}$где интегрирование осуществляется в $t$ космос. Рассмотрим, например, край $i=2$ , затем $F_{2}(t)=x_{3}+t(x_{2}-x_{3})$ с $x_{2}$ и $x_{3}$ обозначающий начало и точки. Для общей 1-формы $\omega ^{1}=a(x)d\xi _{1}+b(x)d\xi _{2}$, человек получает $g_{2}=\int _{0}^{1}\left(a(t){\frac {\partial \xi _{1}}{\partial t}}+b(t){\frac {\partial \xi _{2}}{\partial t}}\right)dt$.