Функция большинства
В логической логике ( функция большинства также называемая медианным оператором ) — это булева функция , которая дает значение false, когда половина или более аргументов являются ложными, и истинным в противном случае, т. е. значение функции равно значению большинства входных данных.
Булевы схемы
[ редактировать ]
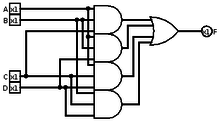
Мажоритарный вентиль — это логический вентиль, используемый для усложнения схем и других приложений булевых схем . Вентиль большинства возвращает истину тогда и только тогда, когда более 50% его входных данных истинны.
Например, в полном сумматоре выходной сигнал переноса находится путем применения мажоритарной функции к трем входам, хотя часто эта часть сумматора разбивается на несколько более простых логических элементов.
Многие системы имеют тройное модульное резервирование ; они используют функцию большинства для декодирования логики большинства для реализации коррекции ошибок .
Главный результат в области сложности схем заключается в том, что мажоритарная функция не может быть вычислена с помощью схем AC0 субэкспоненциального размера.
Характеристики
[ редактировать ]Для любых x , y и z тернарный медианный оператор ⟨ x , y , z ⟩ удовлетворяет следующим уравнениям.
- ⟨x , y , y⟩ = y
- ⟨ Икс , y , z ⟩ знак равно ⟨ z , Икс , y ⟩
- ⟨ Икс , y , z ⟩ знак равно ⟨ Икс , z , y ⟩
- ⟨⟨ Икс , ш , y ⟩, ш , z ⟩ знак равно ⟨ Икс , ш , ⟨ y , ш , z ⟩⟩
Абстрактная система, удовлетворяющая этим аксиомам, является медианной алгеброй .
Галстуки
[ редактировать ]Большинство приложений намеренно используют нечетное количество входных данных, чтобы им не приходилось сталкиваться с вопросом, что происходит, когда ровно половина входных данных равна 0, а ровно половина входных данных равна 1. Немногие системы, которые вычисляют функцию большинства по четному числу входов часто смещены в сторону «0» - они выдают «0», когда ровно половина входов равна 0 - например, мажоритарный вентиль с 4 входами имеет выход 0 только тогда, когда на его входах появляются два или более нуля. [1] В некоторых системах ничья может быть разорвана случайным образом. [2]
Монотонные формулы для большинства
[ редактировать ]Для n = 1 медианный оператор — это просто унарная операция тождества x . Для n = 3 тернарный медианный оператор можно выразить с помощью конъюнкции и дизъюнкции как xy + yz + zx .
Для произвольного n существует монотонная формула для большинства размера O( n 5.3 ). Это доказывается вероятностным методом . Таким образом, эта формула неконструктивна. [3]
Существуют подходы для получения явной формулы для большинства полиномиальных размеров:
- Возьмите медиану из сортировочной сети , где каждый «провод» сравнения и обмена представляет собой просто логический элемент ИЛИ и логический элемент И. Айтай ( АКС ). – Комлос – Семереди Примером может служить строительство
- Объедините выходы меньших мажоритарных схем. [4]
- Дерандомизируйте доказательство Валианта монотонной формулы. [5]
См. также
[ редактировать ]- Булева алгебра (структура)
- Булевы алгебры канонически определены
- Алгоритм большинства голосов Бойера-Мура
- Проблема большинства (клеточный автомат)
Примечания
[ редактировать ]- ^ Петерсон, Уильям Уэсли; Велдон, Э.Дж. (1972). Коды, исправляющие ошибки . МТИ Пресс. ISBN 9780262160391 .
- ^ Чауя, Клодин; Уррад, Уэрдия; Лима, Рикардо (июль 2013 г.). «Правила большинства со случайным разрывом связи в логических сетях регулирования генов» . ПЛОС ОДИН . 8 (7). Публичная научная библиотека: e69626. Бибкод : 2013PLoSO...869626C . дои : 10.1371/journal.pone.0069626 . ПМЦ 3724945 . ПМИД 23922761 .
- ^ Валиант, Лесли (1984). «Короткие монотонные формулы для мажоритарной функции». Журнал алгоритмов . 5 (3): 363–366. дои : 10.1016/0196-6774(84)90016-6 .
- ^ Амано, Казуюки (2018). «Схемы большинства второй глубины для большинства и расширителей списков» . 43-й Международный симпозиум по математическим основам информатики (MFCS 2018) . 117 (81). Schloss Dagstuhl – Leibniz-Zentrum fuer Informatik: 1–13. doi : 10.4230/LIPIcs.MFCS.2018.81 .
- ^ Хори, Шломо; Маген, Авнер; Питасси, Тонианн (2006). «Монотонные схемы для функции большинства» . Аппроксимация, рандомизация и комбинаторная оптимизация. Алгоритмы и методы . Конспекты лекций по информатике. Том. 4110. Спрингер. стр. 410–425. дои : 10.1007/11830924_38 . ISBN 978-3-540-38044-3 .
Ссылки
[ редактировать ]- Кнут, Дональд Э. (2008). Введение в комбинаторные алгоритмы и булевы функции . Искусство компьютерного программирования . Том. 4а. Река Аппер-Сэддл, Нью-Джерси: Аддисон-Уэсли. стр. 64–74. ISBN 978-0-321-53496-5 .
Внешние ссылки
[ редактировать ]![]() СМИ, связанные с функциями большинства, на Викискладе?
СМИ, связанные с функциями большинства, на Викискладе?