Точки и коробки
«Точки и коробки» — игра с карандашом и бумагой для двух игроков (иногда и больше). Впервые оно было опубликовано в 19 веке французским математиком Эдуардом Люка , который назвал его la pipopipette . [1] У него было много других названий, [2] включая точки и тире , игра в точки , [3] сетка точка в точку , [4] коробки , [5] и свиньи в загоне . [6]
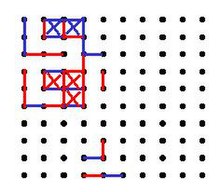
Игра начинается с пустой сетки из точек. Обычно два игрока по очереди добавляют одну горизонтальную или вертикальную линию между двумя несвязанными соседними точками. Игрок, заполнивший четвертую сторону коробки 1×1, зарабатывает одно очко и делает еще один ход. Очко обычно записывается путем размещения отметки, идентифицирующей игрока в поле, например инициала. Игра заканчивается, когда больше нельзя разместить линии. Победителем становится игрок, набравший наибольшее количество очков. [2] [7] Доска может иметь сетку любого размера. Если у вас мало времени или для изучения игры, подойдет доска 2х2 (3х3 точки). [8] С другой стороны, доска 5×5 хороша для экспертов. [9]
Стратегия
[ редактировать ]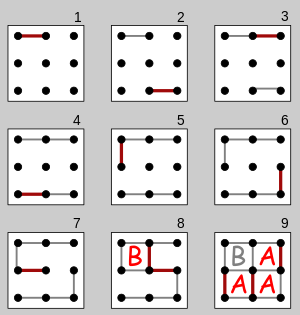
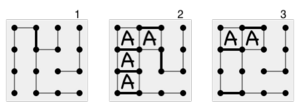
Для большинства начинающих игроков игра начинается с этапа более или менее случайного соединения точек, где единственная стратегия — избегать добавления третьей стороны в какой-либо ящик. Так продолжается до тех пор, пока все оставшиеся (потенциальные) ящики не объединятся в цепочки – группы из одного или нескольких соседних ящиков, в которых любой ход отдает все ящики цепочки противнику. На этом этапе игроки обычно берут все доступные коробки, а затем открывают наименьшую доступную цепочку своему противнику. Например, начинающий игрок, столкнувшийся с ситуацией, подобной позиции 1 на диаграмме справа, в которой можно захватить несколько ящиков, может захватить все ящики в цепочке, что приведет к позиции 2. Но своим последним ходом он открыть следующую, более крупную цепочку, и новичок проигрывает игру. [2] [10]
Более опытный игрок, столкнувшийся с позицией 1, вместо этого будет использовать стратегию двойного креста , взяв все коробки в цепочке, кроме двух, и покинув позицию 3. Противник возьмет эти две коробки, а затем будет вынужден открыть следующую цепочку. Заняв позицию 3, игрок А побеждает. Одна и та же стратегия двойного скрещивания применяется независимо от того, сколько длинных цепочек: игрок, использующий эту стратегию, возьмет все коробки, кроме двух, в каждой цепочке, а также все коробки в последней цепочке. Если цепочки достаточно длинные, то этот игрок выиграет.
Следующий уровень стратегической сложности между экспертами, которые оба использовали бы стратегию двойного креста (если бы им было разрешено), — это битва за контроль: опытный игрок пытается заставить своего противника открыть первую длинную цепочку, потому что игрок тот, кто первым откроет длинную цепочку, обычно проигрывает. [2] [10] Против игрока, который не понимает концепцию жертвы, эксперт просто должен сделать правильное количество жертв, чтобы побудить противника передать ему первую цепочку, достаточно длинную, чтобы обеспечить победу. Если другой игрок также жертвует, эксперт должен дополнительно манипулировать количеством доступных жертв посредством предыдущей игры.
В комбинаторной теории игр «Точки и ящики» являются беспристрастной игрой , и многие позиции можно проанализировать с помощью теории Спрага – Гранди . Однако в «Точках и ящиках» нет обычного игрового соглашения, свойственного большинству беспристрастных игр (где побеждает игрок, сделавший ход последним), что значительно усложняет анализ. [2] [10]
Необычные сетки и варианты
[ редактировать ]В «Точки и квадраты» не обязательно играть на прямоугольной сетке — в нее можно играть на треугольной или шестиугольной сетке. [2]
«Точки и прямоугольники» имеют двойную форму графика , называемую «Струны и монеты». В этой игре используется сеть монет (вершин), соединенных веревками (ребрами). Игроки по очереди перерезают веревку. Когда в результате разреза монета остается без ниток, игрок «забирает» монету и делает еще один ход. Победителем становится игрок, который заберет больше всего монет. В игру «Струны и монеты» можно играть на произвольном графике . [2]
При анализе «Точек и ящиков» игра, которая начинается с уже нарисованных внешних линий, называется шведской доской , а стандартная версия, которая начинается полностью пустой, называется американской доской . Промежуточный вариант, у которого только левая и нижняя стороны начинаются с нарисованных линий, называется исландской доской . [11]
Родственная игра — «Точки» , в которой цветные точки добавляются к пустой сетке и соединяются ими прямой или диагональной линией, пытаясь окружить точки противника.
Ссылки
[ редактировать ]- ^ Лукас, Эдуард (1895), «Пипопипетка: новая игра комбинаций», L'arithmetique agricole , Париж: Gauthier-Villars et fils, стр. 204–209 .
- ^ Jump up to: а б с д и ж г Берлекамп, Элвин Р .; Конвей, Джон Х .; Гай, Ричард К. (1982), «Глава 16: Точки и квадраты», Пути победы в ваших математических играх, Том 2: Игры в частности , Academic Press, стр. 507–550 .
- ^ Холладей, Дж. К. (1966), «Заметки об игре в точки», American Mathematical Monthly , 73 (7): 717–720, doi : 10.2307/2313978 , JSTOR 2313978 , MR 0200068 .
- ^ Суэйн, Хизер (2012), «Сыграйте в эти игры: 101 восхитительное развлечение с использованием предметов повседневного обихода» , Penguin, стр. 160–162, ISBN 9781101585030 .
- ^ Соломон, Эрик (1993), «Коробки: закрывающая игра», Игры с карандашом и бумагой , Dover Publications, Inc., стр. 37–39, ISBN 9780486278728 . Перепечатка публикации Thomas Nelson and Sons 1973 года.
- ^ Кинг, Дэвид К. (1999), Дни гражданской войны: откройте для себя прошлое с помощью захватывающих проектов, игр, занятий и рецептов , Американские дети в истории, том. 4, Уайли, стр. 29–30, ISBN. 9780471246121 .
- ^ Берлекамп, Элвин (2000), Игра в точки и ящики: сложная детская игра , AK Peters, Ltd, ISBN 1-56881-129-2 .
- ^ Берлекамп, Конвей и Гай (1982) , «Игра с 4 ящиками», стр. 513–514.
- ^ Берлекамп (2000) , с. xi: [доска 5×5] «достаточно велика, чтобы быть довольно сложной, и в то же время достаточно мала, чтобы игра была достаточно короткой».
- ^ Jump up to: а б с Уэст, Джулиан (1996), «Игра с точками и квадратами на уровне чемпионата» (PDF) , в книге Новаковски, Ричард (редактор), «Игры без шансов» , Беркли: Публикации MSRI, стр. 79–84 .
- ^ Уилсон, Дэвид, Результаты анализа точек и прямоугольников , Университет Висконсина , получено 7 апреля 2016 г.
Внешние ссылки
[ редактировать ]- Бариле, Маргарита, «Точки и прямоугольники» , MathWorld