Серый график

Серый график
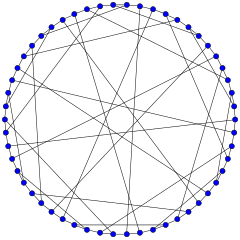Серый график
Назван в честь	Мэрион Кэмерон Грей
Вершины	54
Края	81
Радиус	6
Диаметр	6
Обхват	8
Автоморфизмы	1296
Хроматическое число	2
Хроматический индекс	3
Род	7
Толщина книги	3
Номер очереди	2
Характеристики	Кубический Полусимметричный гамильтониан двусторонний
Таблица графиков и параметров

В математической области теории графов граф Грея представляет собой неориентированный двудольный граф с 54 вершинами и 81 ребром . Это кубический граф : каждая вершина касается ровно трёх ребер. Он был открыт Мэрион К. Грей в 1932 году (неопубликовано), а затем независимо открыт Бауэром в 1968 году в ответ на вопрос, заданный Джоном Фолкманом в 1967 году. Граф Грея интересен как первый известный пример кубического графа, обладающего алгебраическим свойством является реберным, но не транзитивным по вершинам (см. ниже).

Граф Грея имеет хроматическое число 2, хроматический индекс 3, радиус 6 и диаметр 6. Это также с 3 связями вершин и 3 связностями ребер непланарный граф .

Строительство

Сетка 3 × 3 × 3, инцидентность точек и линий которой описывается графом Грея.

Граф с вершинами, упорядоченными и раскрашенными в соответствии с их положением в сетке.

Граф как граф единичных расстояний с 3-кратной вращательной симметрией

Граф Грея можно построить ( Bouwer 1972 ) из ​​27 точек сетки 3 × 3 × 3 и 27 линий, параллельных осям, проходящих через эти точки. Этот набор точек и прямых образует проективную конфигурацию : через каждую точку проходит ровно три прямые, и на каждой прямой находится ровно три точки. Граф Грея — это граф Леви этой конфигурации; у него есть вершина для каждой точки и каждой линии конфигурации, а также ребро для каждой пары точки и линии, соприкасающихся друг с другом. Эта конструкция обобщается (Бауэр, 1972) на любую размерность n ≥ 3, давая n -валентный граф Леви с алгебраическими свойствами, аналогичными свойствам графа Грея. В (Monson, Pisanski, Schulte, Ivic-Weiss 2007) граф Грея появляется как другой вид графа Леви для ребер и треугольных граней некоторого локально тороидального абстрактного регулярного 4-многогранника. Таким образом, он является первым в бесконечном семействе кубических графов, построенных аналогичным образом. Как и другие графы Леви, это двудольный граф , вершины которого соответствуют точкам на одной стороне двудольного деления, а вершины соответствуют линиям на другой стороне.

Марушич и Пизански (2000) предлагают несколько альтернативных методов построения графа Грея. Как и в любом двудольном графе, здесь нет циклов нечётной длины , а также нет циклов из четырёх или шести вершин, поэтому обхват графа Грея равен 8. Простейшая ориентированная поверхность, на которую можно вложить граф Грея, имеет род 7 ( Марушич, Писански и Уилсон, 2005 ).

Граф Грея является гамильтоновым и может быть построен с использованием обозначения LCF :

$[-25,7,-7,13,-13,25]^{9}.\$

Как гамильтонов кубический граф, он имеет хроматический индекс три.

Алгебраические свойства

Группа автоморфизмов графа Грея представляет собой группу порядка 1296. Она действует транзитивно на ребрах графа, но не на его вершинах: существуют симметрии, переводящие каждое ребро в любое другое ребро, но не переводящие каждую вершину в любую другую вершину. Вершины, соответствующие точкам базовой конфигурации, могут быть симметричны только другим вершинам, соответствующим точкам, а вершины, соответствующие линиям, могут быть симметричны только другим вершинам, соответствующим линиям. Следовательно, граф Грея — это полусимметричный граф , наименьший возможный кубический полусимметричный граф.

Характеристический полином графа Грея равен

$(x-3)x^{16}(x+3)(x^{2}-6)^{6}(x^{2}-3)^{12}.\$

Геометрические свойства

Граф Грея можно представить точками на плоскости таким образом, что соседние вершины находятся на единичном расстоянии друг от друга; то есть это граф единичных расстояний .

Ссылки

• Бауэр, И.З. (1968), «Реберный, но не вершинный транзитивный кубический граф», Canadian Mathematical Bulletin , 11 (4): 533–535, doi : 10.4153/CMB-1968-063-0 . (Изак Цурк Бауэр (1933–2012) был профессором УНБ . «Некролог. Исаак Бауэр» . Гражданин Оттавы . 28 декабря 2012. )
• Бауэр, И.З. (1972), «Транзитивные регулярные графы на ребрах, но не на вершинах», Журнал комбинаторной теории, серия B , 12 : 32–40, doi : 10.1016/0095-8956(72)90030-5 .
• Фолкман, Дж. (1967), «Регулярные линейно-симметричные графы», Журнал комбинаторной теории , 3 (3): 533–535, doi : 10.1016/S0021-9800(67)80069-3 .
• Марушич, Драган ; Писански, Томаж (2000), «Возвращение к графу Серого», Журнал теории графов , 35 : 1–7, doi : 10.1002/1097-0118(200009)35:1<1::AID-JGT1>3.0.CO; 2-7 .
• Марушич, Драган ; Писански, Томаж ; Уилсон, Стив (2005), «Род графа Грея равен 7», European Journal of Combinatorics , 26 (3–4): 377–385, doi : 10.1016/j.ejc.2004.01.015 .
• Монсон, Б.; Писански, Т. ; Шульте, Э.; Ивик-Вайс, А. (2007), «Полусимметричные графы из многогранников», Журнал комбинаторной теории, серия A , 114 (3): 421–435, arXiv : math/0606469 , doi : 10.1016/j.jcta.2006.06. 007 , S2CID   10203794

Внешние ссылки

• Вайсштейн, Эрик В. «Серый график» . Математический мир .
• Граф Серого — самый маленький граф такого типа из MathWorld .