Понселе-пойнт

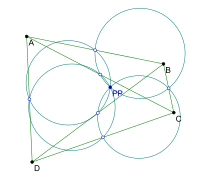
В геометрии точка Понселе из четырех заданных точек определяется следующим образом:

Пусть A, B, C, D — четыре точки плоскости , не образующие ортоцентрической системы и такие, что никакие три из них не лежат на одной прямой . Девятиточечные окружности треугольников △ ABC , △ BCD , △ CDA , △ DAB пересекаются в одной точке — точке Понселе точек A, B, C, D. (Если A, B, C, D образуют ортоцентрическую систему, то треугольники △ ABC , △ BCD , △ CDA , △ DAB имеют один и тот же круг из девяти точек, а точка Понселе не определена.)

Характеристики

Если A, B, C, D окружности, то точка Понселе A, B, C, D лежит на описанной окружности педального треугольника D не лежат на относительно треугольника △ ABC и лежит на других аналогичных окружностях. (Если они действительно лежат на окружности, то эти педальные треугольники будут прямыми; а именно линией Симсона треугольника D относительно треугольника △ ABC и другими аналогичными линиями Симсона. В этом случае эти линии все равно совпадают в точке Понселе. , который также будет антицентром вписанного четырёхугольника с вершинами A, B, C, D .)

Точка Понселе A, B, C, D лежит на окружности через пересечение прямых AB и CD , пересечение прямых AC и BD и пересечение прямых AD и BC (при условии, что все эти пересечения существуют).

Точка Понселе A, B, C, D является центром уникальной прямоугольной гиперболы, проходящей через A, B, C, D.

Ссылки

• Вонк, Ян (2009), «Точка Фейербаха и отражения линии Эйлера» (PDF) , Forum Geometricorum , 9 : 47–55
• Точки Понселе и антигональные сопряжения