Теорема о пицце

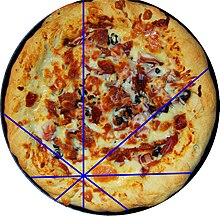
В элементарной геометрии теорема о пицце утверждает равенство двух площадей , возникающих при разделении диска определенным образом.

Теорема названа так потому, что она имитирует традиционную технику нарезки пиццы . Он показывает, что если два человека разделят пиццу, разрезанную на 8 частей (или любое число, кратное 4 больше 8), и возьмут чередующиеся куски, то каждый из них получит одинаковое количество пиццы, независимо от центральной точки разреза.

Заявление

Пусть p — внутренняя точка диска, и пусть n — кратное 4, которое больше или равно 8. Сформируйте n секторов диска с равными углами , выбрав произвольную линию через p , вращая линию ⁠ n / 2 ⁠ − 1 раз на угол ⁠ 2 $π$ / n ⁠ радиан , и разрезав диск по каждому из получившихся ⁠ n / 2 ⁠ линии. Пронумеруйте сектора последовательно по часовой стрелке или против часовой стрелки. Тогда теорема о пицце утверждает, что:

Сумма площадей нечетных секторов равна сумме площадей четных секторов ( Аптон, 1968 ).

История

Теорема о пицце была первоначально предложена Аптоном (1967) как сложная задача . Опубликованное решение этой проблемы Майклом Голдбергом включало прямое манипулирование алгебраическими выражениями для площадей секторов. Картер и Вагон (1994a) предоставляют альтернативное доказательство путем вскрытия . Они показывают, как разделить сектора на более мелкие части так, чтобы каждая часть в секторе с нечетным номером имела конгруэнтную часть в секторе с четным номером, и наоборот. Фредериксон (2012) предоставил семейство доказательств вскрытия для всех случаев (в которых количество секторов равно 8, 12, 16,... ).

Обобщения

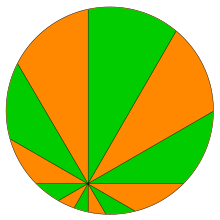
Требование, чтобы количество секторов было кратно четырем, необходимо: как показал Дон Копперсмит , разделение диска на четыре сектора или количество секторов, не делящееся на четыре, обычно не дает равных площадей. Мабри и Дайерманн (2009) ответили на проблему Картера и Вагона (1994b) , предложив более точную версию теоремы, которая определяет, какой из двух наборов секторов имеет большую площадь в тех случаях, когда площади неравны. В частности, если количество секторов равно 2 ( mod 8) и ни один срез не проходит через центр диска, то подмножество секторов, содержащее центр, имеет меньшую площадь, чем другое подмножество, а если количество секторов равно 6 (mod 8) и ни один срез не проходит через центр, то подмножество срезов, содержащее центр, имеет большую площадь. Нечетное количество секторов невозможно при прямолинейных разрезах, а разрез через центр приводит к тому, что два подмножества становятся равными независимо от количества секторов.

Мабри и Дейерманн (2009) также отмечают, что когда пицца разделена поровну, то и ее корочка делится поровну (корку можно интерпретировать либо как периметр диска , либо как область между границей диска и меньшим кругом, имеющим один и тот же центр, причем точка разреза лежит внутри последней), а поскольку диски, ограниченные обеими окружностями, разделены поровну, то и их разница тоже. Однако, когда пицца делится неравномерно, посетитель, которому достается больше площади для пиццы, на самом деле получает наименьшее количество корочки.

Как Хиршхорн и др. (1999) отмечают, что равное деление пиццы также приводит к равному разделению ее начинок, при условии, что каждая начинка распределена по диску (не обязательно концентричному всей пицце), который содержит центральную точку p деления на сектора.

Связанные результаты

Хиршхорн и др. (1999) показывают, что пицца, разрезанная так же, как это указано в теореме о пицце, на количество n секторов с равными углами, где n делится на четыре, также может быть разделена поровну между n /4 людьми. Например, пиццу, разделенную на 12 секторов, могут разделить поровну как три человека, так и двое; однако, чтобы вместить всех пятерых Хиршхорнов, пиццу необходимо разделить на 20 секторов.

Цибулка и др. (2010) и Knauer, Micek & Ueckerdt (2011) изучают теорию игр выбора бесплатных кусков пиццы, чтобы гарантировать большую долю - проблему, поставленную Дэном Брауном и Питером Винклером . В изученном ими варианте задачи пицца нарезается радиально (без гарантии равноугольных секторов), и двое посетителей поочередно выбирают кусочки пиццы, соседствующие с уже съеденным сектором. Если оба посетителя попытаются максимизировать количество съеденной пиццы, посетитель, который возьмет первый кусок, может гарантировать себе 4/9 доли от общего количества пиццы, и существует такой кусок пиццы, что он не может взять больше. Задача справедливого дележа или разрезания торта рассматривает схожие игры, в которых разные игроки имеют разные критерии измерения размера своей доли; например, один посетитель может предпочесть получить как можно больше пепперони, а другой - как можно больше сыра.

Высшие измерения

Браилов (2021) , Браилов (2022) , Эренборг, Морель и Ридди (2022) и Эренборг, Морель и Ридди (2023) распространяют этот результат на более высокие измерения, т.е. для определенных расположений гиперплоскостей попеременная сумма объемов, вырезанных гиперплоскости равна нулю.

Сравните с теоремой о сэндвиче с ветчиной , результатом о нарезке n -мерных объектов. Двумерная версия подразумевает, что любая пицца, какой бы деформированной она ни была, может быть разделена пополам по площади и длине корочки одним тщательно выбранным прямым разрезом. Трехмерная версия подразумевает наличие плоского разреза, в котором поровну используются основа, помидор и сыр.

См. также

Последовательность ленивого поставщика провизии — последовательность , целых чисел подсчитывающая максимальное количество кусков пиццы, которое можно получить из заданного количества прямых ломтиков.

Ссылки

Картер, Ларри; Вагон, Стэн (1994a), «Доказательство без слов: справедливое распределение пиццы», Mathematics Magazine , 67 (4): 267, doi : 10.1080/0025570X.1994.11996228 , JSTOR 2690845 .
Картер, Ларри; Вагон, Стэн (1994b), «Задача 1457», Mathematics Magazine , 67 (4): 303–310, JSTOR 2690855 .
Цибулка, Йозеф; Кынчл, Ян; Месарош, Виола; Столарж, Рудольф; Валтр, Павел (2010), «Решение проблемы пиццы Питера Винклера», Праздник комбинаторики и информатики , Математические исследования Общества Боляи, том. 20, Математическое общество Яноша Бойяи и Springer-Verlag, стр. 63–93, arXiv : 0812.4322 , doi : 10.1007/978-3-642-13580-4_4 , ISBN 978-3-642-13579-8 , S2CID 18272355 .
Браилов, Юрий (2021), «Группы отражений и теорема о пицце» , Алгебра и анализ , 33 (6): 1–8
Браилов Юрий (2022), «Группы отражений и теорема о пицце» , СПб. матем. J. , 33 (6): 891–896, doi : 10.1090/spmj/1732 , S2CID 253334994 .
Эренборг, Ричард; Морель, Софи; Ридди, Маргарет (3 июня 2022 г.), «Разделение пиццы в 𝑛 измерениях» , Transactions of the American Mathematical Society , 375 (8): 5829–5857, arXiv : 2102.06649 , doi : 10.1090/tran/8664 , ISSN 0002-9947
Эренборг, Ричард; Морель, Софи; Ридди, Маргарет (17 октября 2023 г.), «Пицца и 2-структуры», Дискретная и вычислительная геометрия , 70 : 1221–1244, arXiv : 2105.07288 , doi : 10.1007/s00454-023-00600-2
Хиршхорн, Дж.; Хиршхорн, доктор медицины; Хиршхорн, Дж. К.; Хиршхорн, AD; Хиршхорн, ПМ (1999), «Теорема о пицце» (PDF) , Austral. Математика. Соц. Газ. , 26 : 120–121 .
Фредериксон, Грег (2012), «Доказательство в пицце», Mathematics Magazine , 85 (1): 26–33, doi : 10.4169/math.mag.85.1.26 , JSTOR 10.4169/math.mag.85.1.26 , S2CID 116636161 .
Кнауэр, Коля; Мичек, Петр; Укердт, Торстен (2011), «Как съесть 4/9 пиццы», Discrete Mathematics , 311 (16): 1635–1645, arXiv : 0812.2870 , doi : 10.1016/j.disc.2011.03.015 , S2CID 15566728 .
Мабри, Рик; Дайерманн, Пол (2009), «О сыре и корочке: доказательство гипотезы о пицце и другие вкусные результаты», American Mathematical Monthly , 116 (5): 423–438, CiteSeerX 10.1.1.156.4216 , doi : 10.4169/193009709x470317 , JSTOR 40391118 .
Орнес, Стивен (11 декабря 2009 г.), «Идеальный способ нарезать пиццу» , New Scientist .
Аптон, LJ (1967), «Проблема 660», Mathematics Magazine , 40 (3): 163, JSTOR 2688484 . Постановка задачи {{citation}}:CS1 maint:postscript ( ссылка ) .
Аптон, LJ (1968), «Задача 660», Mathematics Magazine , 41 (1): 42, JSTOR 2687962 . Решение Майкла Голдберга {{citation}}:CS1 maint:postscript ( ссылка ) .
Бержени, Джордж (1994), «Теорема о пицце - Часть I» (PDF) , Журнал Quantum : 29
Бержени, Джордж (1994), «Теорема о пицце - Часть II» (PDF) , Журнал Quantum : 29

Внешние ссылки

Вайсштейн, Эрик В. «Теорема о пицце» . Математический мир .
Силке, Торстен, Теорема о пицце , получено 24 ноября 2009 г.