Штраф за разрыв

Штраф за пробел — это метод оценки совпадений двух или более последовательностей. При выравнивании последовательностей введение пробелов в последовательностях может позволить алгоритму выравнивания соответствовать большему количеству терминов, чем выравнивание без пробелов. Однако для создания полезного выравнивания важно свести к минимуму пробелы в выравнивании. Слишком большое количество пробелов может привести к тому, что выравнивание станет бессмысленным. Штрафы за пробелы используются для корректировки оценок выравнивания в зависимости от количества и длины пробелов. Пять основных типов штрафов за пробелы: постоянные, линейные, аффинные, выпуклые и основанные на профилях. ^[1]

Приложения

Выравнивание генетической последовательности . В биоинформатике пробелы используются для учета генетических мутаций, возникающих в результате вставок или делеций в последовательности, иногда называемых инделами . Вставки или делеции могут возникать из-за одиночных мутаций, несбалансированного кроссинговера в мейозе , неправильного спаривания цепей и хромосомной транслокации . ^[2] Идея разрыва в выравнивании важна во многих биологических приложениях, поскольку вставки или делеции составляют целую подпоследовательность и часто происходят в результате одного мутационного события. ^[3] Более того, отдельные мутационные события могут создавать пробелы разного размера. Следовательно, при подсчете баллов пробелы необходимо оценивать как единое целое при выравнивании двух последовательностей ДНК. Если рассматривать несколько пробелов в последовательности как один больший пробел, это уменьшит высокую стоимость мутаций. Например, две белковые последовательности могут быть относительно похожими, но различаться в определенных интервалах, поскольку один белок может иметь субъединицу, отличную от другой. Представление этих различных подпоследовательностей в виде пробелов позволит нам рассматривать эти случаи как «хорошие совпадения», даже если в последовательности есть длинные последовательные прогоны с операциями удаления. Таким образом, использование хорошей модели штрафа за пробелы позволит избежать низких оценок при выравнивании и повысит шансы найти истинное выравнивание. ^[3] При выравнивании генетических последовательностей пробелы обозначаются тире (-) при выравнивании последовательностей белка и ДНК. ^[1]
Unix diff Функция — вычисляет минимальную разницу между двумя файлами аналогично обнаружению плагиата.
Проверка орфографии . Штрафы за пробелы могут помочь найти правильно написанные слова с кратчайшим расстоянием редактирования до слова с ошибкой. Пробелы могут указывать на пропущенную букву в неправильно написанном слове.
Обнаружение плагиата . Штрафы за пробелы позволяют алгоритмам обнаруживать плагиат в разделах документа, помещая пробелы в исходные разделы и сопоставляя идентичные разделы. Штраф за пробел для определенного документа определяет, какая часть данного документа, вероятно, является оригинальной или плагиатом.

Приложения биоинформатики

Глобальное выравнивание

Глобальное выравнивание выполняет сквозное выравнивание последовательности запроса с ссылочной последовательностью. В идеале этот метод выравнивания наиболее подходит для близкородственных последовательностей одинаковой длины. Алгоритм Нидлмана-Вунша — это метод динамического программирования, используемый для глобального выравнивания. По сути, алгоритм делит проблему на набор подзадач, а затем использует результаты подзадач для восстановления решения исходного запроса. ^[4]

Полуглобальное выравнивание

Полуглобальное выравнивание используется для поиска конкретного совпадения в большой последовательности. Пример включает поиск промоторов в последовательности ДНК. В отличие от глобального выравнивания, оно исключает отсутствие разрывов на концах в одной или обеих последовательностях. Если концевые пробелы наказываются в одной последовательности 1, но не в последовательности 2, получается выравнивание, содержащее последовательность 2 внутри последовательности 1.

Локальное выравнивание

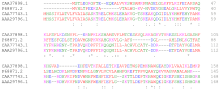
Локальное выравнивание последовательностей сопоставляет непрерывный подраздел одной последовательности со смежным подразделом другой. ^[5] Алгоритм Смита-Уотермана основан на выставлении оценок за совпадения и несоответствия. Совпадения увеличивают общий балл совпадения, тогда как несовпадения уменьшают балл. Тогда хорошее выравнивание получает положительную оценку, а плохое — отрицательную. Локальный алгоритм находит выравнивание с наивысшим баллом, рассматривая только совпадения с положительными оценками и выбирая из них лучшее. Алгоритм представляет собой алгоритм динамического программирования . При сравнении белков используется матрица сходства, которая присваивает балл каждой возможной паре остатков. Оценка должна быть положительной для схожих остатков и отрицательной для пар несходных остатков. Пробелы обычно наказываются с использованием линейной функции разрыва, которая назначает первоначальный штраф за открытие пробела и дополнительный штраф за расширение пробела, увеличивая длину пробела.

Матрица оценок

Матрицы замен, такие как BLOSUM, используются для выравнивания последовательностей белков. ^[6] Матрица замен присваивает балл за выравнивание любой возможной пары остатков. ^[6] В общем, различные матрицы замен предназначены для обнаружения сходства между последовательностями, которые расходятся в разной степени. Одна матрица может быть достаточно эффективной в относительно широком диапазоне эволюционных изменений. ^[6] Матрица BLOSUM-62 является одной из лучших матриц замещения для обнаружения слабых сходств белков. ^[6] Матрицы BLOSUM с высокими номерами предназначены для сравнения близкородственных последовательностей, а матрицы с низкими номерами — для сравнения отдаленно родственных последовательностей. Например, BLOSUM-80 используется для выравниваний, более похожих по последовательности, а BLOSUM-45 используется для выравниваний, которые расходятся друг от друга. ^[6] При особенно длинных и слабых выравниваниях наилучшие результаты может дать матрица BLOSUM-45. Короткие выравнивания легче обнаружить, используя матрицу с более высокой «относительной энтропией», чем у BLOSUM-62. В серию BLOSUM не входят матрицы с относительной энтропией, подходящие для самых коротких запросов. ^[6]

Индельс

Во время репликации ДНК клеточный механизм репликации склонен совершать ошибки двух типов при дублировании ДНК. Эти две ошибки репликации представляют собой вставки и удаления отдельных оснований ДНК из цепи ДНК (инделы). ^[7] Инделы могут иметь серьезные биологические последствия, вызывая мутации в цепи ДНК, которые могут привести к инактивации или чрезмерной активации целевого белка. Например, если в кодирующей последовательности происходит инделия из одного или двух нуклеотидов, результатом будет сдвиг рамки считывания или мутация сдвига рамки считывания , которая может сделать белок неактивным. ^[7] Биологические последствия инделей часто бывают пагубными и часто связаны с такими патологиями, как рак . Однако не все индели являются мутациями сдвига рамки считывания. Если инделы возникают в тринуклеотидах, результатом является расширение последовательности белка, что также может влиять на функцию белка. ^[7]

Типы

Постоянный

Это простейший тип штрафа за пропуск: каждому пробелу присваивается фиксированная отрицательная оценка, независимо от его длины. ^[3]^[8] Это побуждает алгоритм делать меньше промежутков большего размера, оставляя более крупные смежные секции.

ATTGACCTGA
||   |||||
AT---CCTGA

Выравнивание двух коротких последовательностей ДНК, где «-» обозначает разрыв в одну пару оснований. Если каждое совпадение приносило 1 очко, а весь разрыв -1, то общий счет: 7 − 1 = 6.

Линейный

По сравнению со штрафом за постоянный пропуск, штраф за линейный пропуск учитывает длину (L) каждой вставки/удаления в пропуске. Следовательно, если штраф за каждый вставленный/удаленный элемент равен B, а длина пробела L; общий штраф за пропуск будет произведением двух BL. ^[9] Этот метод предпочитает более короткие пробелы, при этом общий балл уменьшается с каждым дополнительным пробелом.

ATTGACCTGA
||   |||||
AT---CCTGA

В отличие от постоянного штрафа за разрыв, учитывается размер разрыва. При совпадении со счетом 1 и каждым разрывом -1 счет здесь равен (7 − 3 = 4).

Аффинный

Наиболее широко используемой функцией штрафа за пропуск является аффинный штраф за пропуск. Штраф за аффинный пропуск объединяет компоненты как постоянного, так и линейного штрафа за пропуск, принимая форму $A+B\cdot (L-1)$ . Это вводит новые термины: A известен как штраф за открытие пробела, B - штраф за расширение пробела и L - длина пробела. Открытие гэпа относится к затратам, необходимым для открытия гэпа любой длины, а расширение гэпа — к стоимости увеличения длины существующего гэпа на 1. ^[10] Часто неясно, какими должны быть значения A и B, поскольку они различаются в зависимости от цели. В общем, если интерес состоит в том, чтобы найти близкородственные совпадения (например, удаление векторной последовательности во время секвенирования генома), следует использовать более высокий штраф за пробел, чтобы уменьшить количество пробелов. С другой стороны, штраф за разрыв должен быть снижен, если вы заинтересованы в поиске более отдаленного совпадения. ^[9] Отношения между A и B также влияют на размер разрыва. Если размер зазора важен, используется маленький A и большой B (расширение зазора обходится дороже), и наоборот. Важно только соотношение A/B, так как оба умножаются на одну и ту же положительную константу. $k$ увеличит все штрафы на $k$ : $kA+kB(L-1)=k(A+B(L-1))$ что не меняет относительный штраф между различными выравниваниями.

Выпуклый

Использование штрафа за аффинный разрыв требует назначения фиксированных значений штрафа как за открытие, так и за расширение разрыва. Это может быть слишком жестко для использования в биологическом контексте. ^[11]

Логарифмический разрыв принимает вид $G(L)=A+C\ln L$ и был предложен, поскольку исследования показали, что распределение размеров инделей подчиняется степенному закону. ^[12] Другая предлагаемая проблема с использованием аффинных пробелов - это предпочтение выравнивания последовательностей с более короткими пробелами. Штраф за логарифмический разрыв был изобретен, чтобы изменить аффинный разрыв так, чтобы желательны длинные пробелы. ^[11] Однако, в отличие от этого, было обнаружено, что использование логарифматических моделей приводит к плохому выравниванию по сравнению с аффинными моделями. ^[12]

На основе профиля

Алгоритмы выравнивания профиля-профиля являются мощными инструментами для обнаружения отношений гомологии белков с повышенной точностью выравнивания. ^[13] Выравнивание профиля-профиля основано на статистических профилях частоты indel из нескольких выравниваний последовательностей, полученных с помощью поиска PSI-BLAST. ^[13] Вместо использования матриц замен для измерения сходства пар аминокислот, методы выравнивания профиля-профиля требуют оценочной функции на основе профиля для измерения сходства пар векторов профиля. ^[13] При выравнивании профиля-профиля используются функции штрафа за зазоры. Информация о пробелах обычно используется в форме профилей частот, которые более специфичны для выравниваемых последовательностей. ClustalW и MAFFT приняли этот вид определения штрафа за пропуск для своих множественных выравниваний последовательностей. ^[13] Точность выравнивания можно повысить с помощью этой модели, особенно для белков с низкой идентичностью последовательностей. Некоторые алгоритмы выравнивания профилей также используют информацию о вторичной структуре как один термин в своих оценочных функциях, что повышает точность выравнивания. ^[13]

Сравнение временных сложностей

Использование выравнивания в вычислительной биологии часто включает в себя последовательности различной длины. Важно выбрать модель, которая будет эффективно работать при известном размере входных данных. Время, необходимое для запуска алгоритма, называется временной сложностью.

Временные сложности для различных моделей штрафов за пропуски
Тип	Время
Штраф за постоянный разрыв	О(мин)
Штраф за аффинный разрыв	О(мин)
Штраф за выпуклый зазор	O(mn lg(m+n))

Проблемы

Есть несколько проблем, когда дело доходит до работы с пробелами. При работе с популярными алгоритмами, по-видимому, существует мало теоретической основы для формы штрафных функций за пропуск. ^[14] Следовательно, для любой ситуации выравнивания размещение зазора должно определяться эмпирически. ^[14] Кроме того, штрафы за пробелы в парном выравнивании, такие как штраф за пробелы в аффинном выравнивании, часто реализуются независимо от типов аминокислот во вставленном или удаленном фрагменте или на разорванных концах, несмотря на доказательства того, что определенные типы остатков являются предпочтительными в областях пробелов. ^[14] Наконец, выравнивание последовательностей предполагает выравнивание соответствующих структур, однако взаимосвязи между структурными особенностями пробелов в белках и соответствующими им последовательностями известны лишь недостаточно. Из-за этого сложно включить структурную информацию в штрафы за пробелы. ^[14] Некоторые алгоритмы используют прогнозируемую или фактическую структурную информацию для смещения расположения пробелов. Однако только меньшинство последовательностей имеет известные структуры, и большинство проблем выравнивания связаны с последовательностями неизвестной вторичной и третичной структуры. ^[14]

Ссылки

^ Перейти обратно: ^а ^б «Глоссарий» . Розалинда . Команда Розалинда . Проверено 20 мая 2021 г.
^ Кэрролл, Ридж, Клемент, Снелл, Хайрам, Перри, Марк, Куинн (1 января 2007 г.). «Последствия штрафов за открытие и расширение разрыва» . Международный журнал исследований и приложений в области биоинформатики . Проверено 9 сентября 2014 г. {{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )
^ Перейти обратно: ^а ^б ^с «Штраф за пробел» (PDF) . Алгоритмы молекулярной биологии . 01 января 2006 г. Архивировано из оригинала (PDF) 26 июня 2013 г. Проверено 13 сентября 2014 г.
^ Леск, Артур М. (26 июля 2013 г.). «биоинформатика» . Британская энциклопедия . Проверено 12 сентября 2014 г.
^ Вингрон, М.; Уотерман, М.С. (1994). «Выравнивание последовательностей и выбор штрафа. Обзор концепций, тематических исследований и последствий». Журнал молекулярной биологии . 235 (1): 1–12. дои : 10.1016/S0022-2836(05)80006-3 . ПМИД 8289235 .
^ Перейти обратно: ^а ^б ^с ^д ^и ^ж «Матрицы замены BLAST» . НКБИ . Проверено 27 ноября 2012 г.
^ Перейти обратно: ^а ^б ^с Гарсиа-Диас, Мигель (2006). «Механизм генетического глиссандо: структурная биология индель-мутаций». Тенденции биохимических наук . 31 (4): 206–214. дои : 10.1016/j.tibs.2006.02.004 . ПМИД 16545956 .
^ «Глоссарий — Штраф за постоянный пробел» . Розалинда . Команда Розалинда. 12 августа 2014 г. Проверено 12 августа 2014 г.
^ Перейти обратно: ^а ^б Ходжман С., Френч А., Вестхед Д. (2009). BIOS Instant Notes в биоинформатике . Гирляндная наука. стр. 143–144. ISBN 978-0203967249 .
^ «Глобальное выравнивание с оценочной матрицей и штрафом за аффинный разрыв» . Розалинда . Команда Розалинда. 2 июля 2012 г. Проверено 12 сентября 2014 г.
^ Перейти обратно: ^а ^б Сун, Винг-Кин (2011). Алгоритмы в биоинформатике: практическое введение . ЦРК Пресс. стр. 42–47. ISBN 978-1420070347 .
^ Перейти обратно: ^а ^б Картрайт, Рид (5 декабря 2006 г.). «Затраты на логарифмический зазор снижают точность выравнивания» . БМК Биоинформатика . 7 : 527. дои : 10.1186/1471-2105-7-527 . ПМК 1770940 . ПМИД 17147805 .
^ Перейти обратно: ^а ^б ^с ^д ^и Ван С, Ян RX, Ван XF, Си Цзинь, Чжан Цз (12 октября 2011 г.). «Сравнение штрафов за линейные зазоры и штрафы за переменные зазоры на основе профиля при выравнивании профиля-профиля». Вычислительная биол. хим . 35 (5): 308–318. doi : 10.1016/j.compbiolchem.2011.07.006 . ПМИД 22000802 .
^ Перейти обратно: ^а ^б ^с ^д ^и Врабль Ю.О., Гришин Н.В. (1 января 2004 г.). «Пробелы в структурно подобных белках: на пути к улучшению множественного выравнивания последовательностей». Белки . 54 (1): 71–87. дои : 10.1002/прот.10508 . ПМИД 14705025 . S2CID 20474119 .

Дальнейшее чтение

Тейлор В.Р., Манро Р.Э. (1997). «Множественная последовательность потоков: размещение условного разрыва» . Сложите Дес . 2 (4): С33-9. дои : 10.1016/S1359-0278(97)00061-8 . ПМИД 9269566 .
Тейлор В.Р. (1996). «Нелокальный штраф за зазор за выравнивание профиля». Бычья Математика Биол . 58 (1): 1–18. дои : 10.1007/BF02458279 . ПМИД 8819751 . S2CID 189884646 .
Вингрон М., Уотерман М.С. (1994). «Выравнивание последовательностей и выбор штрафа. Обзор концепций, тематических исследований и последствий». Дж Мол Биол . 235 (1): 1–12. дои : 10.1016/S0022-2836(05)80006-3 . ПМИД 8289235 .
Панюков В.В. (1993). «Нахождение устойчивых совпадений: сходство и расстояние». Компьютерные приложения и биологические науки . 9 (3): 285–90. дои : 10.1093/биоинформатика/9.3.285 . ПМИД 8324629 .
Александров Н.Н. (1992). «Локальное множественное выравнивание по матрице консенсуса». Компьютерные приложения и биологические науки . 8 (4): 339–45. дои : 10.1093/биоинформатика/8.4.339 . ПМИД 1498689 .
Хейн Дж (1989). «Новый метод, который одновременно выравнивает и реконструирует предковые последовательности для любого количества гомологичных последовательностей, когда задана филогения» . Мол Биол Эвол . 6 (6): 649–68. doi : 10.1093/oxfordjournals.molbev.a040577 . ПМИД 2488477 .
Хеннеке CM (1989). «Алгоритм множественного выравнивания последовательностей для гомологичных белков с использованием информации о вторичной структуре и, при необходимости, выравнивания ключей по функционально важным сайтам». Компьютерные приложения и биологические науки . 5 (2): 141–50. дои : 10.1093/биоинформатика/5.2.141 . ПМИД 2751764 .
Райх Дж.Г., Драбш Х., Даумлер А. (1984). «О статистической оценке сходства последовательностей ДНК» . Нуклеиновые кислоты Рез . 12 (13): 5529–43. дои : 10.1093/нар/12.13.5529 . ПМК 318937 . ПМИД 6462914 .

[rosalind_glossary-1] Перейти обратно: ^а ^б «Глоссарий» . Розалинда . Команда Розалинда . Проверено 20 мая 2021 г.

[2] Кэрролл, Ридж, Клемент, Снелл, Хайрам, Перри, Марк, Куинн (1 января 2007 г.). «Последствия штрафов за открытие и расширение разрыва» . Международный журнал исследований и приложений в области биоинформатики . Проверено 9 сентября 2014 г. {{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )

[:0-3] Перейти обратно: ^а ^б ^с «Штраф за пробел» (PDF) . Алгоритмы молекулярной биологии . 01 января 2006 г. Архивировано из оригинала (PDF) 26 июня 2013 г. Проверено 13 сентября 2014 г.

[4] Леск, Артур М. (26 июля 2013 г.). «биоинформатика» . Британская энциклопедия . Проверено 12 сентября 2014 г.

[5] Вингрон, М.; Уотерман, М.С. (1994). «Выравнивание последовательностей и выбор штрафа. Обзор концепций, тематических исследований и последствий». Журнал молекулярной биологии . 235 (1): 1–12. дои : 10.1016/S0022-2836(05)80006-3 . ПМИД 8289235 .

[NCBI-6] Перейти обратно: ^а ^б ^с ^д ^и ^ж «Матрицы замены BLAST» . НКБИ . Проверено 27 ноября 2012 г.

[Garcia-Diaz2006-7] Перейти обратно: ^а ^б ^с Гарсиа-Диас, Мигель (2006). «Механизм генетического глиссандо: структурная биология индель-мутаций». Тенденции биохимических наук . 31 (4): 206–214. дои : 10.1016/j.tibs.2006.02.004 . ПМИД 16545956 .

[8] «Глоссарий — Штраф за постоянный пробел» . Розалинда . Команда Розалинда. 12 августа 2014 г. Проверено 12 августа 2014 г.

[Hodgman_C,_French_A,_Westhead_D,_2009_143–144-9] Перейти обратно: ^а ^б Ходжман С., Френч А., Вестхед Д. (2009). BIOS Instant Notes в биоинформатике . Гирляндная наука. стр. 143–144. ISBN 978-0203967249 .

[10] «Глобальное выравнивание с оценочной матрицей и штрафом за аффинный разрыв» . Розалинда . Команда Розалинда. 2 июля 2012 г. Проверено 12 сентября 2014 г.

[:1-11] Перейти обратно: ^а ^б Сун, Винг-Кин (2011). Алгоритмы в биоинформатике: практическое введение . ЦРК Пресс. стр. 42–47. ISBN 978-1420070347 .

[:2-12] Перейти обратно: ^а ^б Картрайт, Рид (5 декабря 2006 г.). «Затраты на логарифмический зазор снижают точность выравнивания» . БМК Биоинформатика . 7 : 527. дои : 10.1186/1471-2105-7-527 . ПМК 1770940 . ПМИД 17147805 .

[pmid22000802-13] Перейти обратно: ^а ^б ^с ^д ^и Ван С, Ян RX, Ван XF, Си Цзинь, Чжан Цз (12 октября 2011 г.). «Сравнение штрафов за линейные зазоры и штрафы за переменные зазоры на основе профиля при выравнивании профиля-профиля». Вычислительная биол. хим . 35 (5): 308–318. doi : 10.1016/j.compbiolchem.2011.07.006 . ПМИД 22000802 .

[pmid14705025-14] Перейти обратно: ^а ^б ^с ^д ^и Врабль Ю.О., Гришин Н.В. (1 января 2004 г.). «Пробелы в структурно подобных белках: на пути к улучшению множественного выравнивания последовательностей». Белки . 54 (1): 71–87. дои : 10.1002/прот.10508 . ПМИД 14705025 . S2CID 20474119 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]