Деконволюция Ричардсона – Люси

Не путать с модифицированной итерацией Ричардсона .

Использование деконволюции Ричардсона-Люси для восстановления сигнала, размытого функцией импульсного отклика.

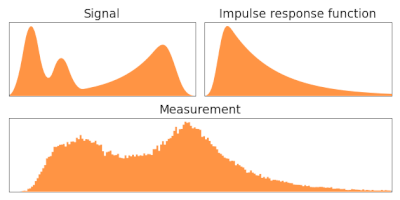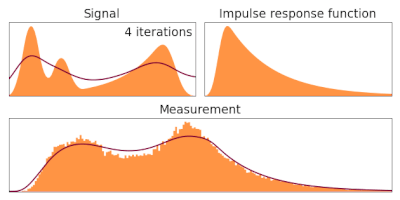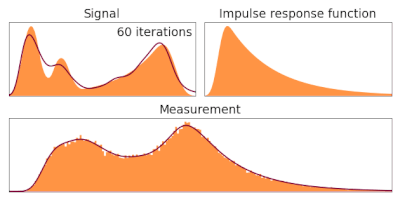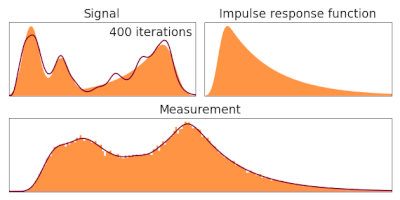
Алгоритм Ричардсона-Люси , также известный как деконволюция Люси-Ричардсона , представляет собой итеративную процедуру восстановления основного изображения, которое было размыто известной функцией распределения точек . Он был назван в честь Уильяма Ричардсона и Леона Б. Люси , которые описали его независимо.

Описание

Когда изображение создается с помощью оптической системы и обнаруживается с помощью фотопленки или устройства с зарядовой связью , например, , оно неизбежно оказывается размытым, при этом идеальный точечный источник не выглядит как точка, а распределяется в так называемую точку. функция распространения. Расширенные источники можно разложить на сумму множества отдельных точечных источников, таким образом, наблюдаемое изображение можно представить в виде матрицы перехода p, действующей на базовое изображение:

$d_{i}=\sum _{j}p_{i,j}u_{j}\,$

где $u_{j}$ это интенсивность основного изображения в пикселе $j$ и $d_{i}$ обнаруженная интенсивность в пикселе $i$. В общем случае матрица, элементы которой $p_{i,j}$ описывает часть света от исходного пикселя j, которая обнаруживается в пикселе i. В большинстве хороших оптических систем (или, вообще, линейных систем, которые описываются как инвариантные к сдвигу ) передаточная функция p может быть выражена просто через пространственное смещение между исходным пикселем j и пикселем наблюдения i:

$p_{i,j}=P(i-j)$

где $P(\Delta i)$ называется функцией рассеяния точки . В этом случае приведенное выше уравнение становится сверткой . Это было написано для одного пространственного измерения, но большинство систем визуализации являются двумерными: источник, обнаруженное изображение и функция рассеяния точки имеют два индекса. Таким образом, двумерное обнаруженное изображение представляет собой свертку основного изображения с двумерной функцией распределения точек. $P(\Delta x,\Delta y)$ плюс добавленный шум обнаружения.

Чтобы оценить $u_{j}$ учитывая наблюдаемое $d_{i}$ и известный $P(\Delta i_{x},\Delta j_{y})$, применяется следующая итерационная процедура, в оценивается которой $u_{j}$ (называется ${\hat {u}}_{j}^{(t)}$) для номера итерации t обновляется следующим образом:

${\hat {u}}_{j}^{(t+1)}={\hat {u}}_{j}^{(t)}\sum _{i}{\frac {d_{i}}{c_{i}}}p_{ij}$

где

$c_{i}=\sum _{j}p_{ij}{\hat {u}}_{j}^{(t)}$

и $\sum _{j}p_{ij}=1$ предполагается. Эмпирически было показано, что если эта итерация сходится, она сходится к решению максимального правдоподобия для $u_{j}$.

Записав это в более общем плане для двух (или более) измерений в терминах свертки с функцией распределения точки P:

${\hat {u}}^{(t+1)}={\hat {u}}^{(t)}\cdot \left({\frac {d}{{\hat {u}}^{(t)}\otimes P}}\otimes P^{*}\right)$

где деление и умножение являются поэлементными, $\otimes$ указывает на двумерную свертку, а $P^{*}$ — функция распространения перевернутой точки.

В задачах, где функция рассеяния точки $p_{ij}$ неизвестно априори , была предложена модификация алгоритма Ричардсона-Люси для выполнения слепой деконволюции .

Вывод

В контексте флуоресцентной микроскопии вероятность измерения набора количества фотонов (или цифр оцифровки, пропорционального обнаруженному свету). $\mathbf {m} =[m_{0},...,m_{K}]$ для ожидаемых значений $\mathbf {E} =[E_{0},...,E_{K}]$ для детектора с $K+1$ пикселей определяется выражением

$P(\mathbf {m} \vert \mathbf {E} )=\prod _{i}^{K}\mathrm {Poisson} (E_{i})=\prod _{i}^{K}{\frac {{E_{i}}^{m_{i}}e^{-E_{i}}}{m_{i}!}}$

с ним удобно работать $\ln(P)$ поскольку в контексте оценки максимального правдоподобия цель состоит в том, чтобы найти максимум функции правдоподобия, не заботясь о ее абсолютном значении.

$\ln(P(m\vert E))=\sum _{i}^{K}\left[(m_{i}\ln E_{i}-E_{i})-\ln(m_{i}!)\right]$

Опять же с тех пор $\ln(m_{i}!)$ является константой, никакой дополнительной информации о положении максимума она не даст, поэтому учитывайте

$\alpha (m\vert E)=\sum _{i}^{K}\left[m_{i}\ln E_{i}-E_{i}\right]$

где $\alpha$ это что-то, что находится в той же максимальной позиции, что и $P(m\vert E)$. Теперь подумайте, что $E$ исходит из основной истины $x$ и измерение $\mathbf {H}$ который предполагается линейным. Затем

$\mathbf {E} =\mathbf {H} \mathbf {x}$

где подразумевается матричное умножение. Это также можно записать в форме

$E_{m}=\sum _{n}^{K}H_{mn}x_{n}$

где можно увидеть, как $H$, смешивает или размывает основную истину.

Можно также показать, что производная элемента $\mathbf {E}$, $(E_{i})$ по отношению к какому-либо другому элементу $x$ можно записать как:

${\frac {\partial E_{i}}{\partial x_{j}}}=H_{ij}$ ( 1 )

Совет: в этом легко убедиться, написав матрицу $\mathbf {H}$ скажем (5 x 5) и два массива $\mathbf {E}$ и $\mathbf {x}$ из 5 элементов и проверьте это. Это последнее уравнение можно интерпретировать как количество одного элемента $\mathbf {x}$, скажем, элемент $i$ влияет на другие элементы $j\neq i$ (и конечно дело $i=j$ тоже учитывается). Например, в типичном случае элемент основной истины $\mathbf {x}$ будет влиять на близлежащие элементы в $\mathbf {E}$ но не очень далекие (значение $0$ ожидается на этих элементах матрицы).

Теперь ключевой и произвольный шаг: $x$ неизвестно, но может быть оценено ${\hat {\mathbf {x} }}$, позвоним ${\hat {\mathbf {x} _{old}}}$ и ${\hat {\mathbf {x} _{new}}}$ предполагаемые основные истины при использовании алгоритма RL, где символ шляпы используется, чтобы отличить основную истину от оценки основной истины

${\hat {x}}_{new}={\hat {x}}_{old}+\lambda {\frac {\partial \ \alpha (m\vert E(x))}{\partial x}}|_{{\hat {x}}_{old}}$ ( 2 )

Где ${\frac {\partial }{\partial x}}$ означает $K$-мерный градиент. Выполняя частную производную от $\alpha (m\vert E(x))$ дает следующее выражение

${\frac {\partial \ \alpha (m\vert E(x))}{\partial x_{j}}}={\frac {\partial }{\partial x_{j}}}\sum _{i}^{K}\left[m_{i}\ln E_{i}-E_{i}\right]=\sum _{i}^{K}\left[{\frac {m_{i}}{E_{i}}}{\frac {\partial }{\partial x_{j}}}E_{i}-{\frac {\partial }{\partial x_{j}}}E_{i}\right]=\sum _{i}^{K}{\frac {\partial E_{i}}{\partial x_{j}}}\left[{\frac {m_{i}}{E_{i}}}-1\right]$

Подставив ( 1 ), получим, что

${\frac {\partial \ \alpha (m\vert E(x))}{\partial x_{j}}}=\sum _{i}^{K}H_{ij}\left[{\frac {m_{i}}{E_{i}}}-1\right]$

Обратите внимание, что ${H}_{ji}^{T}=H_{ij}$ по определению транспонирования матрицы. И следовательно

${\frac {\partial \ \alpha (m\vert E(x))}{\partial x_{j}}}=\sum _{i}^{K}{H}_{ji}^{T}\left[{\frac {m_{i}}{E_{i}}}-1\right]$ ( 3 )

Поскольку это уравнение справедливо для всех $j$ охватывающий все элементы из $1$ к $K$, эти $K$ уравнения можно компактно переписать в виде одного векторного уравнения

${\frac {\partial \ \alpha (m\vert \mathbf {E} (x))}{\partial x}}={\mathbf {H} ^{T}}\left[{\frac {\mathbf {m} }{\mathbf {E} }}-\mathbf {1} \right]$

где $\mathbf {H} ^{T}$ представляет собой матрицу и $m$, $E$ и $\mathbf {1}$ являются векторами. Теперь в качестве, казалось бы, произвольного, но ключевого шага, позвольте

$\lambda ={\frac {{\hat {\mathbf {x} }}_{old}}{\mathbf {H} ^{T}\mathbf {1} }}$ ( 4 )

где $\mathbf {1}$ представляет собой вектор единиц размера $K$ (то же самое, что $m$, $E$ и $x$) и деление поэлементное. Используя ( 3 ) и ( 4 ), ( 2 ) можно переписать как

${\hat {\mathbf {x} }}_{new}={\hat {\mathbf {x} }}_{old}+\lambda {\frac {\partial \alpha (\mathbf {m} \vert \mathbf {E} (x))}{\partial x}}={\hat {\mathbf {x} }}_{old}+{\frac {{\hat {\mathbf {x} }}_{old}}{{\mathbf {H} ^{T}}\mathbf {1} }}{\mathbf {H} ^{T}}\left[{\frac {\mathbf {m} }{\mathbf {E} }}-\mathbf {1} \right]={\hat {\mathbf {x} }}_{old}+{\frac {{\hat {\mathbf {x} }}_{old}}{\mathbf {H} ^{T}\mathbf {1} }}\mathbf {H} ^{T}{\frac {\mathbf {m} }{\mathbf {E} }}-{\hat {\mathbf {x} }}_{old}$

что дает

${\hat {\mathbf {x} }}_{new}={\hat {\mathbf {x} }}_{old}\mathbf {H} ^{T}\left({\frac {\mathbf {m} }{\mathbf {E} }}\right)/\mathbf {H} ^{T}\mathbf {1}$ ( 5 )

Где деление относится к поэлементному матричному делению и $\mathbf {H} ^{T}$ работает как матрица, но деление и продукт (неявно после ${\hat {\mathbf {x} }}_{old}$) являются поэлементными. Также, $\mathbf {E} =E({\hat {\mathbf {x} }}_{old})=\mathbf {H} {\hat {x}}_{old}$ можно вычислить, поскольку предполагается, что

- Первоначальное предположение ${\hat {\mathbf {x} }}_{0}$ известно (и обычно считается экспериментальными данными)

- измерения Функция $\mathbf {H}$ известен

С другой стороны $\mathbf {m}$ это экспериментальные данные. Таким образом, уравнение ( 5 ), применяемое последовательно, обеспечивает алгоритм для оценки нашей основной истины. $\mathbf {x} _{new}$ по возрастанию (поскольку оно движется в направлении градиента правдоподобия) в ландшафте правдоподобия . В этом выводе не было продемонстрировано, что он сходится, и не показано никакой зависимости от первоначального выбора. Обратите внимание, что уравнение ( 2 ) позволяет следовать направлению, которое увеличивает вероятность, но выбор логарифмической производной является произвольным. С другой стороны, уравнение ( 4 ) вводит способ взвешивания движения с предыдущего шага итерации. Обратите внимание, что если бы этот член не присутствовал в ( 5 ), то алгоритм вывел бы движение в оценке, даже если $\mathbf {m} =E({\hat {\mathbf {x} }}_{old})$. Стоит отметить, что единственная стратегия, используемая здесь, — это максимизировать вероятность любой ценой, чтобы на изображении могли появиться артефакты. Стоит отметить, что никаких предварительных знаний о форме основной истины нет. $\mathbf {x}$ используется в этом выводе.

Программное обеспечение

• RawTherapee (начиная с версии 2.3)

См. также

• Деконволюция
• Фильтр Винера (деконволюция при наличии аддитивного шума)