Функция распределения точек

Формирование изображения в конфокальном микроскопе : центральный продольный (XZ) срез. Полученное трехмерное распределение получается в результате свертки реальных источников света с PSF.

Точечный источник , изображенный системой с отрицательной (вверху), нулевой (в центре) и положительной (внизу) сферической аберрацией . Изображения слева расфокусированы внутрь, изображения справа — наружу.

Функция рассеяния точки ( PSF ) описывает реакцию системы сфокусированного оптического изображения на точечный источник или точечный объект. системы Более общий термин для PSF — это импульсный отклик ; PSF - это импульсная характеристика или функция импульсной характеристики (IRF) системы сфокусированной оптической визуализации. PSF во многих контекстах можно рассматривать как расширенное пятно на изображении, которое представляет собой один точечный объект, который рассматривается как пространственный импульс. С функциональной точки зрения это версия оптической передаточной функции (OTF) системы формирования изображений в пространственной области (т. е. обратное преобразование Фурье) . Это полезная концепция в оптике Фурье , астрономической визуализации , медицинской визуализации , электронной микроскопии и других методах визуализации, таких как трехмерная микроскопия (например, в конфокальной лазерной сканирующей микроскопии ) и флуоресцентная микроскопия .

Степень расплывчатости (размытия) изображения точечного объекта для системы формирования изображения является мерой качества системы формирования изображения. В системах некогерентной визуализации , таких как флуоресцентные микроскопы , телескопы или оптические микроскопы, процесс формирования изображения линеен по интенсивности изображения и описывается теорией линейных систем . Это означает, что когда два объекта A и B отображаются одновременно с помощью системы некогерентной визуализации, результирующее изображение равно сумме независимо отображаемых объектов. Другими словами: на изображение A не влияет изображение B и наоборот , из-за свойства невзаимодействия фотонов. В пространственно-инвариантных системах, т. е. в тех, в которых PSF одинаков во всем пространстве изображения, изображение сложного объекта представляет собой свертку этого объекта и PSF. PSF можно получить из дифракционных интегралов.

Введение

В силу свойства линейности оптических некогерентных систем формирования изображений, т.е.

Изображение ( Объект ₁ + Объект ₂ ) = Изображение ( Объект ₁ ) + Изображение ( Объект ₂ )

изображение объекта в микроскопе или телескопе как некогерентной системе формирования изображений можно вычислить, выразив поле плоскости объекта как взвешенную сумму двумерных импульсных функций, а затем выразив поле плоскости изображения как взвешенную сумму изображений . этих импульсных функций. Это известно как принцип суперпозиции , справедливый для линейных систем . Изображения отдельных импульсных функций объектной плоскости называются функциями рассеяния точки (PSF), что отражает тот факт, что математическая точка света в объектной плоскости распространяется , образуя конечную область в плоскости изображения. (В некоторых разделах математики и физики их можно назвать функциями Грина или функциями импульсного отклика . PSF считаются функциями импульсного отклика для систем визуализации.

Применение PSF: деконволюция математически смоделированного PSF и изображения с низким разрешением повышает разрешение.

Когда объект делится на дискретные точечные объекты различной интенсивности, изображение вычисляется как сумма PSF каждой точки. Поскольку PSF обычно полностью определяется системой формирования изображения (то есть микроскопом или телескопом), все изображение можно описать, зная оптические свойства системы. Этот процесс визуализации обычно формулируется уравнением свертки . В обработке изображений микроскопа и астрономии знание PSF измерительного устройства очень важно для восстановления (исходного) объекта с помощью деконволюции . В случае лазерных лучей PSF можно математически смоделировать, используя концепции гауссовых лучей . Например, деконволюция математически смоделированного PSF и изображения улучшает видимость особенностей и удаляет шум изображения.

Теория

Функция распространения точки может быть независимой от положения в плоскости объекта, и в этом случае она называется инвариантом сдвига . Кроме того, если в системе нет искажений, координаты плоскости изображения линейно связаны с координатами плоскости объекта через увеличение M как:

$(x_{i},y_{i})=(Mx_{o},My_{o})$.

Если система формирования изображений создает перевернутое изображение, мы можем просто рассматривать оси координат плоскости изображения как противоположные осям плоскости объекта. При этих двух предположениях, т. е. о том, что PSF инвариантен к сдвигу и что искажений нет, вычисление интеграла свертки плоскости изображения является простым процессом.

Математически мы можем представить поле объектной плоскости как:

$O(x_{o},y_{o})=\iint O(u,v)~\delta (x_{o}-u,y_{o}-v)~du\,dv$

т.е. как сумма взвешенных импульсных функций, хотя на самом деле это просто констатация свойства сдвига двумерных дельта-функций (подробнее обсуждается ниже). Переписывание функции пропускания объекта в приведенном выше виде позволяет рассчитать поле плоскости изображения как суперпозицию изображений каждой из отдельных импульсных функций, т.е. как суперпозицию над взвешенными функциями разброса точек в плоскости изображения с использованием той же весовой функции. как и в предметной плоскости, т.е. $O(x_{o},y_{o})$. Математически изображение выражается как:

$I(x_{i},y_{i})=\iint O(u,v)~\mathrm {PSF} (x_{i}/M-u,y_{i}/M-v)\,du\,dv$

в котором ${\textstyle {\mbox{PSF}}(x_{i}/M-u,y_{i}/M-v)}$ – образ импульсной функции $\delta (x_{o}-u,y_{o}-v)$.

Двумерную импульсную функцию можно рассматривать как предел (поскольку размер стороны w стремится к нулю) функции «квадратного столба», показанной на рисунке ниже.

Функция квадратного поста

Мы представляем, что плоскость объекта разбивается на такие квадратные области, как эта, каждая из которых имеет свою собственную функцию квадратного столба. Если высота h поддерживается на уровне 1/w столба ² , тогда, когда размер стороны w стремится к нулю, высота h стремится к бесконечности таким образом, что объем (интеграл) остается постоянным и равен 1. Это придает 2D-импульсу свойство смещения (которое подразумевается в уравнении выше ), в котором говорится, что когда двумерная импульсная функция δ( x − u , y − v ) интегрируется с любой другой непрерывной функцией f ( u , v ) , она «отсеивает» значение f в месте расположения импульс, т. е. в точке ( x , y ) .

Концепция идеального точечного источника является центральной в идее PSF. Однако в природе не существует идеального математического излучателя точечного источника; эта концепция совершенно нефизическая и представляет собой скорее математическую конструкцию, используемую для моделирования и понимания систем оптического изображения. Полезность концепции точечного источника заключается в том, что точечный источник в плоскости двумерного объекта может излучать только идеальную сферическую волну с одинаковой амплитудой - волну, имеющую идеально сферические, распространяющиеся наружу фазовые фронты с одинаковой интенсивностью повсюду на сферах ( см. принцип Гюйгенса-Френеля ). Такой источник однородных сферических волн показан на рисунке ниже. Мы также отметим, что идеальный излучатель точечного источника будет излучать не только однородный спектр распространяющихся плоских волн, но и однородный спектр экспоненциально затухающих ( затухающих ) волн, и именно они ответственны за разрешение меньше одной длины волны (см. Фурье-оптика ). Это следует из следующего Выражение преобразования Фурье для двумерной импульсной функции,

$\delta (x,y)\propto \iint e^{j(k_{x}x+k_{y}y)}\,dk_{x}\,dk_{y}$

Усечение сферической волны линзой

Квадратичная линза перехватывает часть этой сферической волны и перефокусирует ее в размытую точку в плоскости изображения. Для одной линзы точечный источник на оси в плоскости объекта создает PSF диска Эйри в плоскости изображения. Можно показать (см. оптику Фурье , принцип Гюйгенса-Френеля , дифракцию Фраунгофера ), что поле, излучаемое плоским объектом (или, по принципу взаимности, поле, сходящееся к плоскому изображению), связано с соответствующей ему плоскостью источника (или изображения). распределение через соотношение преобразования Фурье (FT). Кроме того, равномерная функция по круговой области (в одной области ФТ) соответствует J ₁ ( x )/ x в другой области ФТ, где J ₁ ( x ) первого порядка — функция Бесселя первого рода. То есть равномерно освещенная круглая апертура, через которую проходит сходящаяся однородная сферическая волна, дает изображение диска Эйри в фокальной плоскости. График образца диска Эйри показан на рисунке рядом.

Воздушный диск

Следовательно, сходящаяся ( частичная ) сферическая волна, показанная на рисунке выше, создает диск Эйри в плоскости изображения. Аргумент функции J ₁ ( x )/ x важен, поскольку он определяет масштаб диска Эйри (другими словами, насколько велик диск в плоскости изображения). Если Θ _max — максимальный угол, который сходящиеся волны образуют с осью линзы, r — радиальное расстояние в плоскости изображения и волновое число k = 2π/λ, где λ = длина волны, то аргумент функции: kr tan(Θ _Макс ) . Если Θ _max мало (только небольшая часть сходящейся сферической волны доступна для формирования изображения), то радиальное расстояние r должно быть очень большим, прежде чем полный аргумент функции отойдет от центрального пятна. Другими словами, если Θ _max Гейзенберга мало, диск Эйри велик (что является еще одним утверждением принципа неопределенности для пар преобразований Фурье, а именно, что малая протяженность в одной области соответствует широкой протяженности в другой области, и эти два значения равны связанные через произведение пространственной пропускной способности ). В силу этого системы с большим увеличением , которые обычно имеют небольшие значения Θ _max (по условию синуса Аббе ), могут иметь большее размытие изображения из-за более широкого PSF. Размер PSF пропорционален увеличению , так что размытие не хуже в относительном смысле, но определенно хуже в абсолютном.

На рисунке выше показано усечение падающей сферической волны линзой. Для измерения функции рассеяния точки (или функции импульсного отклика) линзы не требуется идеальный точечный источник, излучающий идеальную сферическую волну во всех направлениях пространства. Это связано с тем, что линза имеет только конечную (угловую) полосу пропускания или конечный угол пересечения. Таким образом, любая угловая полоса пропускания, содержащаяся в источнике и выходящая за пределы краевого угла линзы (т. е. лежащая за пределами полосы пропускания системы), по существу является пустой полосой пропускания источника, поскольку линза не может перехватить ее для обработки. В результате для измерения идеальной функции рассеяния точки не требуется идеальный точечный источник. Все, что нам нужно, это источник света, который имеет по крайней мере такую ​​же угловую полосу пропускания, как и тестируемая линза (и, конечно же, однороден в этом угловом секторе). Другими словами, нам нужен только точечный источник, который создается сходящейся (однородной) сферической волной, полуугол которой больше краевого угла линзы.

Из-за внутреннего ограниченного разрешения систем визуализации измеренные PSF не свободны от неопределенности. При визуализации желательно подавить боковые лепестки визуализирующего луча с помощью методов аподизации . В случае систем передачи изображений с гауссовым распределением луча PSF моделируется следующим уравнением:

$\mathrm {PSF} (f,z)=I_{r}(0,z,f)\exp \left[-z\alpha (f)-{\dfrac {2\rho ^{2}}{0.36{\frac {cka}{{\text{NA}}f}}{\sqrt {{1+\left({\frac {2\ln 2}{c\pi }}\left({\frac {\text{NA}}{0.56k}}\right)^{2}fz\right)}^{2}}}}}\right],$

где коэффициент k зависит от коэффициента усечения и уровня освещенности, NA — числовая апертура, c — скорость света, f — частота фотонов визуализирующего луча, I _r — интенсивность опорного луча, a — корректировка фактор и $\rho$ — радиальное положение центра луча на соответствующей плоскости z .

История и методы

Дифракционная теория функций рассеяния точки была впервые изучена Эйри в девятнадцатом веке. Он разработал выражение для амплитуды и интенсивности функции рассеяния точки идеального инструмента, свободного от аберраций (так называемого диска Эйри ). Теория аберрированных функций рассеяния точки вблизи оптимальной фокальной плоскости изучалась Цернике и Нейбоером в 1930–40-х годах. Центральную роль в их анализе играют круговые полиномы Цернике , которые позволяют эффективно представить аберрации любой оптической системы с вращательной симметрией. Недавние аналитические результаты позволили расширить подход Нейбоера и Цернике для оценки функции рассеяния точки на большой объем вокруг оптимальной фокусной точки. Эта расширенная теория Нейбура-Цернике (ENZ) позволяет изучать несовершенное изображение трехмерных объектов в конфокальной микроскопии или астрономии в неидеальных условиях изображения. Теория ENZ также применялась для характеристики оптических инструментов с точки зрения их аберрации путем измерения распределения интенсивности в фокусе и решения соответствующего уравнения. обратная задача .

Приложения

микроскопия

Пример экспериментально полученной функции рассеяния точки, полученной с помощью конфокального микроскопа с использованием масляного объектива 63x 1,4NA. Он был создан с использованием программного обеспечения деконволюции Huygens Professional. Показаны виды в форматах xz, xy, yz и трехмерное представление.

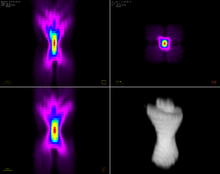
В микроскопии экспериментальное определение PSF требует источников излучения субразрешения (точечных). квантовые точки и флуоресцентные шарики . Для этой цели обычно рассматривают С другой стороны, теоретические модели, описанные выше, позволяют детально рассчитать PSF для различных условий визуализации. Обычно предпочтительна наиболее компактная ограниченная дифракцией форма PSF, . Однако, используя соответствующие оптические элементы (например, пространственный модулятор света ), форму PSF можно спроектировать для различных применений.

Астрономия

Функция рассеяния точки космического телескопа Хаббл до камеры WFPC внесения поправок в ее оптическую систему.

В наблюдательной астрономии экспериментальное определение PSF часто бывает очень простым из-за большого количества точечных источников ( звезд или квазаров ). Форма и источник PSF могут сильно различаться в зависимости от инструмента и контекста, в котором он используется.

Для радиотелескопов и с дифракционным ограничением космических телескопов доминирующие члены PSF могут быть выведены из конфигурации апертуры в области Фурье . На практике различные компоненты сложной оптической системы могут включать несколько членов. Полное описание PSF также будет включать диффузию света (или фотоэлектронов) в детекторе, а также ошибки отслеживания в космическом корабле или телескопе.

Для наземных оптических телескопов атмосферная турбулентность (известная как астрономическое видение вклад в PSF доминирует ). При наземных изображениях с высоким разрешением PSF часто меняется в зависимости от положения на изображении (эффект, называемый анизопланатизмом). В наземных системах адаптивной оптики PSF представляет собой комбинацию апертуры системы с остаточными нескорректированными атмосферными условиями.

Литография

Перекрывающиеся пики PSF. Когда пики расположены примерно на расстоянии ~ 1 длины волны/числовая апертура, они эффективно сливаются. В этот момент FWHM составляет ~ 0,6 длины волны/числовую апертуру.

PSF также является фундаментальным ограничением для обычного сфокусированного изображения отверстия. при этом минимальный размер печати находится в диапазоне 0,6-0,7 длины волны/числовая апертура, где числовая апертура системы формирования изображений. Например, в случае системы EUV с длиной волны 13,5 нм и NA = 0,33 минимальный размер отдельного отверстия, которое можно визуализировать, находится в диапазоне 25-29 нм. Маска фазового сдвига имеет края фазы под углом 180 градусов, что обеспечивает более высокое разрешение.

Офтальмология

Функции распределения точек в последнее время стали полезным диагностическим инструментом в клинической офтальмологии . Состояние пациентов измеряется с помощью Шака-Гартмана датчика волнового фронта , а специальное программное обеспечение рассчитывает PSF для глаза этого пациента. Этот метод позволяет врачу смоделировать потенциальное лечение пациента и оценить, как это лечение повлияет на PSF пациента. Кроме того, после измерения PSF можно минимизировать с помощью системы адаптивной оптики. Это, в сочетании с камерой CCD и системой адаптивной оптики, можно использовать для визуализации анатомических структур, которые иначе не видны in vivo , таких как конусные фоторецепторы.

См. также

• Воздушный диск
• Круг замешательства для тесно связанной темы в общей фотографии.
• Деконволюция
• Окруженная энергия
• Функция импульсного отклика
• Микроскоп
• Микросфера
• ПСФ Лаборатория

Ссылки

• Хагай Киршнер; Франсуа Аге; Дэниел Сейдж; Майкл Унсер (2013). «3-D PSF-приспособление для флуоресцентной микроскопии: применение и локализация» (PDF) . Журнал микроскопии . 249 (январь 2013 г.): 13–25. дои : 10.1111/j.1365-2818.2012.03675.x . ПМИД   23126323 . S2CID   5318333 .
• Рэйчел Ноек; Калеб Норншильд; Джастин Мигач; Тэхён Ким; Питер Маунц; Тру Меррилл; Харли Хейден; КС Пай; Юнгсан Ким (2010). «Многомасштабная оптика для улучшенного сбора света от точечного источника» (PDF) . Оптические письма . 35 (июнь 2010 г.): 2460–2. arXiv : 1006.2188 . Бибкод : 2010OptL...35.2460N . дои : 10.1364/OL.35.002460 . hdl : 10161/4222 . ПМИД   20634863 . S2CID   6838852 .