Гауссов пучок

Мгновенное абсолютное значение действительной части амплитуды электрического поля гауссова пучка ТЕМ ₀₀ , фокальная область. Показаны $|{\mathcal {Re}}(E(t_{1}))|$ таким образом, с двумя пиками для каждого положительного волнового фронта .

Вверху: поперечный профиль интенсивности гауссова луча, распространяющегося за пределы страницы. Синяя кривая: зависимость амплитуды электрического (или магнитного) поля от радиального положения от оси луча. Черная кривая — соответствующая интенсивность.

Зеленый лазерный луч мощностью 5 мВт, показывающий _{TEM 00.} профиль

В оптике — гауссов пучок идеализированный пучок , электромагнитного излучения которого огибающая амплитуды в поперечной плоскости задаётся функцией Гаусса ; это также подразумевает гауссовский профиль интенсивности (излучения). Эта фундаментальная (или TEM ₀₀ ) поперечная гауссовая мода описывает предполагаемую мощность многих лазеров , поскольку такой луч меньше расходится и может быть сфокусирован лучше, чем любой другой. Когда гауссов луч перефокусируется идеальной линзой , образуется новый гауссов луч. Профили амплитуд электрического и магнитного поля вдоль кругового гауссова луча заданной длины волны и поляризации определяются двумя параметрами: перетяжкой w ₀ , которая является мерой ширины луча в его самой узкой точке, и положением z относительно талия.

Поскольку функция Гаусса бесконечна по размеру, идеальных гауссовских лучей в природе не существует, и края любого такого луча будут обрезаны любой конечной линзой или зеркалом. Однако гауссиан является полезным приближением к реальному лучу в тех случаях, когда линзы или зеркала в луче значительно больше размера пятна w ( z ) луча.

По сути, гауссиан является решением осевого уравнения Гельмгольца , волнового уравнения для электромагнитного поля. Хотя существуют и другие решения, гауссовы семейства решений полезны для задач, связанных с компактными балками.

Математическая форма

В приведенных ниже уравнениях предполагается, что балка имеет круглое поперечное сечение при всех значениях z ; в этом можно убедиться, заметив, что появляется единственный поперечный размер r . Балки с эллиптическим поперечным сечением или с перетяжками в разных положениях по z для двух поперечных размеров ( астигматические балки) также могут быть описаны как гауссовы балки, но с разными значениями w ₀ и положения z = 0 для двух поперечных измерений. размеры х и у .

Гауссов профиль интенсивности луча с w ₀ = 2 λ .

Гауссов пучок представляет собой поперечную электромагнитную (ПЭМ) моду . Математическое выражение для амплитуды электрического поля является решением параксиального уравнения Гельмгольца . Предполагая поляризацию в направлении x и распространение в направлении + z , электрическое поле в векторных (комплексных) обозначениях определяется как:

$${\mathbf {E} (r,z)}=E_{0}\,{\hat {\mathbf {x} }}\,{\frac {w_{0}}{w(z)}}\exp \left({\frac {-r^{2}}{w(z)^{2}}}\right)\exp \left(\!-i\left(kz+k{\frac {r^{2}}{2R(z)}}-\psi (z)\right)\!\right)$$

где

• r — радиальное расстояние от центральной оси балки,
• z - осевое расстояние от фокуса луча (или «талии»),
• я — мнимая единица ,
• k = 2 πn / λ — волновое число (в радианах в свободном пространстве на метр) для длины волны λ , а n — показатель преломления среды, в которой распространяется луч,
• E ₀ = E (0, 0) — амплитуда электрического поля в начале координат ( r = 0 , z = 0 ),
• w ( z ) — радиус, на котором амплитуды поля падают до 1/ e от их осевых значений (т. е. где значения интенсивности падают до 1/ e ² их осевых значений), в плоскости z вдоль балки,
• w ₀ = w (0) – радиус талии ,
• R ( z ) — радиус кривизны луча волновых фронтов в точке z , а
• ψ ( z ) — фаза Гуи в точке z , дополнительный фазовый член помимо того, который относится к фазовой скорости света.

Физическое электрическое поле получается из приведенной выше амплитуды векторного поля путем умножения действительной части амплитуды на временной коэффициент: $$\mathbf {E} _{\text{phys}}(r,z,t)=\operatorname {Re} (\mathbf {E} (r,z)\cdot e^{i\omega t}),$$где ${\textstyle \omega }$ — угловая частота света, а t — время. Фактор времени предполагает произвольное соглашение о знаках , как обсуждалось в разделе Математическое описание непрозрачности § Комплексно-сопряженная неоднозначность .

Поскольку это решение основано на параксиальном приближении, оно не является точным для очень сильно расходящихся лучей. Приведенная выше форма справедлива в большинстве практических случаев, когда w ₀ ≫ λ / n .

Соответствующее распределение интенсивности (или освещенности ) определяется выражением

$$I(r,z)={|E(r,z)|^{2} \over 2\eta }=I_{0}\left({\frac {w_{0}}{w(z)}}\right)^{2}\exp \left({\frac {-2r^{2}}{w(z)^{2}}}\right),$$

где константа η — волновое сопротивление среды, в которой распространяется луч. Для свободного пространства η = η ₀ ≈ 377 Ом. я ₀ = | Е ₀ | ² /2 η — интенсивность в центре луча на его перетяжке.

Если P ₀ — полная мощность луча, $$I_{0}={2P_{0} \over \pi w_{0}^{2}}.$$

Изменение ширины луча

Функция Гаусса имеет 1/ e ² диаметр ( 2w , как указано в тексте) примерно в 1,7 раза больше FWHM .

В положении z вдоль луча (измеренном от фокуса) параметр размера пятна w определяется гиперболическим соотношением : $$w(z)=w_{0}\,{\sqrt {1+{\left({\frac {z}{z_{\mathrm {R} }}}\right)}^{2}}},$$где $$z_{\mathrm {R} }={\frac {\pi w_{0}^{2}n}{\lambda }}$$называется диапазоном Рэлея , как обсуждается ниже, и $n$ – показатель преломления среды.

Радиус луча w ( z ) в любой позиции z вдоль луча связан с полной шириной на полувысоте (FWHM) распределения интенсивности в этом положении согласно: $$w(z)={\frac {{\text{FWHM}}(z)}{\sqrt {2\ln 2}}}.$$

Кривизна волнового фронта

Кривизна волновых фронтов наибольшая на расстоянии Рэлея, z = ± z _R , по обе стороны от перетяжки, пересекая ноль на самой перетяжке. За пределами расстояния Рэлея | г | > z _R , оно снова уменьшается по величине, приближаясь к нулю при z → ±∞ . Кривизну часто выражают через обратную величину R , радиус кривизны ; для фундаментального гауссова луча кривизна в положении z определяется выражением:

$${\frac {1}{R(z)}}={\frac {z}{z^{2}+z_{\mathrm {R} }^{2}}},$$

поэтому радиус кривизны R ( z ) равен $$R(z)=z\left[{1+{\left({\frac {z_{\mathrm {R} }}{z}}\right)}^{2}}\right].$$Будучи обратной величиной кривизны, радиус кривизны меняет знак и становится бесконечным в перетяжке балки, где кривизна проходит через ноль.

Эллиптические и астигматические лучи

Многие лазерные лучи имеют эллиптическое поперечное сечение. Также распространены балки с положением перетяжки, которые различны для двух поперечных размеров, называемые астигматическими балками. С этими лучами можно иметь дело, используя два приведенных выше уравнения эволюции, но с разными значениями каждого параметра для x и y и разными определениями точки z = 0 . Фаза Гуи представляет собой единое значение, правильно рассчитанное путем суммирования вклада каждого измерения, при этом фаза Гуи находится в диапазоне ± π /4, вносимая каждым измерением.

Эллиптический луч меняет коэффициент эллиптичности по мере распространения от дальнего поля к перетяжке. Размер, который был больше вдали от талии, возле талии будет меньше.

Гауссиан как разложение на моды

Произвольные решения параксиального уравнения Гельмгольца можно разложить как сумму мод Эрмита-Гаусса (чьи профили амплитуды разделяются по x и y с использованием декартовых координат ), мод Лагерра-Гаусса (профили амплитуды которых разделяются по r и θ с использованием цилиндрических координат). ) или аналогично комбинациям мод Инса – Гаусса (профили амплитуд которых разделяются по ξ и η с использованием эллиптических координат ). В любой точке луча z эти моды включают в себя тот же коэффициент Гаусса, что и основная гауссова мода, умножая дополнительные геометрические коэффициенты для указанной моды. Однако разные моды распространяются с разной фазой Гуи , поэтому чистый поперечный профиль из-за суперпозиции мод развивается по z , тогда как распространение любой отдельной моды Эрмита-Гаусса (или Лагерра-Гаусса) сохраняет ту же форму вдоль луча.

Хотя существуют и другие модальные разложения , гауссианы полезны для задач, связанных с компактными пучками, то есть там, где оптическая мощность довольно тесно ограничена вдоль оси. Даже если лазер не лазера. работает в основной гауссовой моде, его мощность обычно будет определяться среди мод низшего порядка с использованием этого разложения, поскольку пространственная протяженность мод более высокого порядка будет иметь тенденцию выходить за пределы резонатора (резонатора) . «Гауссов луч» обычно подразумевает излучение, ограниченное основной (ТЕМ ₀₀ ) гауссовой модой.

Параметры луча

Геометрическая зависимость полей гауссова луча определяется длиной волны света λ ( в диэлектрической среде, если не в свободном пространстве) и следующими параметрами луча , все из которых связаны, как подробно описано в следующих разделах.

Пучковая талия

См. Также: Диаметр луча.

Гауссова ширина луча w ( z ) как функция расстояния z вдоль луча, образующего гиперболу . w ₀ : перетяжка пучка; б : глубина фокуса; z _R : диапазон Рэлея ; Θ : общий угловой разброс

Форма гауссова луча заданной длины волны λ определяется только одним параметром — перетяжкой луча w ₀ . Это мера размера луча в точке его фокуса ( z = 0 в приведенных выше уравнениях), где ширина луча w ( z ) (как определено выше) является наименьшей (и аналогичным образом, когда интенсивность на оси ( r = 0 ) является наибольшим). Из этого параметра определяются другие параметры, описывающие геометрию балки. Сюда входят диапазон Рэлея z _R и асимптотическая расходимость луча θ , как подробно описано ниже.

Диапазон Рэлея и конфокальный параметр

Основная статья: длина Рэлея

Расстояние Рэлея или диапазон Рэлея z _R определяется с учетом размера перетяжки гауссова луча:

$$z_{\mathrm {R} }={\frac {\pi w_{0}^{2}n}{\lambda }}.$$

Здесь λ — длина волны света, n — показатель преломления. На расстоянии от перетяжки, равном диапазону Рэлея z _R , ширина w луча на √ 2 больше, чем в фокусе, где w = w ₀ , перетяжка луча. Это также означает, что интенсивность на оси ( r = 0 ) составляет половину пиковой интенсивности (при z = 0 ). В этой точке луча кривизна волнового фронта ( 1/ R ) наибольшая.

Расстояние между двумя точками z = ± z _R называется конфокальным параметром или глубиной фокуса луча.

Расходимость луча

Дополнительная информация: Расходимость луча.

Хотя хвосты функции Гаусса на самом деле никогда не достигают нуля, для целей последующего обсуждения «краем» балки считается радиус, где r = w ( z ) . Именно здесь интенсивность упала до 1/ e ² его значения на оси. Теперь при z ≫ z _R параметр w ( z ) увеличивается линейно с z . Это значит, что вдали от перетяжки «край» пучка (в указанном выше смысле) имеет конусообразную форму. Угол между этим конусом (чей r = w ( z ) ) и осью луча ( r = 0 ) определяет расходимость луча: $$\theta =\lim _{z\to \infty }\arctan \left({\frac {w(z)}{z}}\right).$$

В параксиальном случае, как мы уже рассматривали, θ (в радианах) тогда приблизительно равно $$\theta ={\frac {\lambda }{\pi nw_{0}}}$$

где n — показатель преломления среды, через которую распространяется луч, а λ — длина волны в свободном пространстве. Тогда общий угловой разброс расходящегося луча или угол при вершине описанного выше конуса определяется выражением $$\Theta =2\theta \,.$$

Тогда этот конус содержит 86% общей мощности гауссова луча.

Поскольку расходимость обратно пропорциональна размеру пятна, для данной длины волны λ гауссовский луч, сфокусированный в небольшое пятно, быстро расходится по мере распространения от фокуса. И наоборот, чтобы минимизировать расходимость лазерного луча в дальней зоне (и увеличить его пиковую интенсивность на больших расстояниях), он должен иметь большое поперечное сечение ( w ₀ ) в перетяжке (и, следовательно, большой диаметр в месте запуска, поскольку w ( z ) никогда не меньше w ₀ ). Эта связь между шириной луча и расходимостью является фундаментальной характеристикой дифракции и преобразования Фурье, которое описывает дифракцию Фраунгофера . Луч с любым заданным профилем амплитуды также подчиняется этой обратной зависимости, но фундаментальная гауссова мода представляет собой особый случай, когда произведение размера луча в фокусе и расходимости в дальней зоне меньше, чем в любом другом случае.

Поскольку модель гауссова луча использует параксиальное приближение, она не работает, когда волновые фронты наклонены более чем на 30 ° от оси луча. Из приведенного выше выражения для расходимости это означает, что модель гауссова луча точна только для балок с перетяжкой, превышающей примерно 2 λ / π .

Качество лазерного луча количественно оценивается произведением параметров луча (BPP). Для гауссова луча BPP является произведением расходимости луча и размера перетяжки w ₀ . BPP реального луча получается путем измерения минимального диаметра луча и расходимости в дальней зоне и их произведения. Отношение BPP реального луча к BPP идеального гауссова луча на той же длине волны известно как M. ² (« М в квадрате »). Их ​ ² для гауссова пучка один. Все реальные лазерные лучи имеют M ² значения больше единицы, хотя лучи очень высокого качества могут иметь значения, очень близкие к единице.

Числовая апертура гауссова луча определяется как NA = n sin θ , где n — показатель преломления среды, через которую распространяется луч. Это означает, что диапазон Рэлея связан с числовой апертурой соотношением $$z_{\mathrm {R} }={\frac {nw_{0}}{\mathrm {NA} }}.$$

Фаза Гуи

Фаза Гуи представляет собой фазовый сдвиг, постепенно приобретаемый лучом вокруг фокальной области. В позиции z фаза Гуи фундаментального гауссова пучка определяется выражением $$\psi (z)=\arctan \left({\frac {z}{z_{\mathrm {R} }}}\right).$$

Фаза Гуи.

Фаза Гуи приводит к увеличению видимой длины волны вблизи перетяжки ( z ≈ 0 ). Таким образом, фазовая скорость в этой области формально превышает скорость света. Это парадоксальное поведение следует понимать как явление ближнего поля , когда отклонение от фазовой скорости света (как это было бы применимо точно к плоской волне) очень мало, за исключением случая луча с большой числовой апертурой , и в этом случае кривизна волновых фронтов (см. предыдущий раздел) существенно меняется на расстоянии одной длины волны. Во всех случаях волновое уравнение удовлетворяется в каждой позиции.

Знак фазы Гуи зависит от соглашения о знаках, выбранного для вектора электрического поля. С е ^iωt зависимости фаза Гуи меняется от - π /2 до + π /2 , а при e ^{- iωt} зависимости она меняется от + π /2 до - π /2 вдоль оси.

Для фундаментального гауссова луча фаза Гуи приводит к чистому расхождению фазы по отношению к скорости света, составляющему π радиан (таким образом, обращение фазы) при движении от дальнего поля на одной стороне перетяжки к дальнему полю на другая сторона. Это изменение фазы не наблюдается в большинстве экспериментов. Однако это имеет теоретическое значение и принимает более широкий диапазон для гауссовских мод более высокого порядка .

Мощность и интенсивность

Питание через отверстие

Для луча, центрированного на апертуре , мощность P, проходящая через круг радиуса r в поперечной плоскости в положении z, равна $$P(r,z)=P_{0}\left[1-e^{-2r^{2}/w^{2}(z)}\right],$$где $$P_{0}={\frac {1}{2}}\pi I_{0}w_{0}^{2}$$– полная мощность, передаваемая лучом.

Для круга радиуса r = w ( z ) доля мощности, передаваемая через круг, равна $${\frac {P(z)}{P_{0}}}=1-e^{-2}\approx 0.865.$$

Аналогично, около 90% мощности луча будет проходить через круг радиуса r = 1,07 × w ( z ) , 95 % — через круг радиуса r = 1,224 × w ( z ) и 99 % — через круг радиуса r. знак равно 1,52 × ш ( z ) .

Пиковая интенсивность

Пиковую интенсивность на осевом расстоянии z от перетяжки луча можно рассчитать как предел заключенной мощности внутри круга радиуса r , разделенный на площадь круга πr. ² как круг сужается: $$I(0,z)=\lim _{r\to 0}{\frac {P_{0}\left[1-e^{-2r^{2}/w^{2}(z)}\right]}{\pi r^{2}}}.$$

Предел можно оценить по правилу Лопиталя : $$I(0,z)={\frac {P_{0}}{\pi }}\lim _{r\to 0}{\frac {\left[-(-2)(2r)e^{-2r^{2}/w^{2}(z)}\right]}{w^{2}(z)(2r)}}={2P_{0} \over \pi w^{2}(z)}.$$

Комплексный параметр луча

Основная статья: Комплексный параметр луча

Размер пятна и кривизна гауссова луча как функция z вдоль луча также могут быть закодированы в комплексном параметре луча q ( z ) предоставлено: $$q(z)=z+iz_{\mathrm {R} }.$$

Обратная величина q ( z ) содержит кривизну волнового фронта и относительную интенсивность на оси в его действительной и мнимой частях соответственно:

$${1 \over q(z)}={1 \over R(z)}-i{\lambda \over n\pi w^{2}(z)}.$$

Комплексный параметр луча упрощает математический анализ распространения гауссова луча, особенно при анализе полостей оптических резонаторов с использованием матриц переноса лучей .

Тогда, используя эту форму, более раннее уравнение для электрического (или магнитного) поля значительно упрощается. Если мы назовем u относительной напряженностью поля эллиптического гауссова луча (с эллиптическими осями в направлениях x и y ), то его можно разделить по x и y согласно: $$u(x,y,z)=u_{x}(x,z)\,u_{y}(y,z),$$

где $${\begin{aligned}u_{x}(x,z)&={\frac {1}{\sqrt {{q}_{x}(z)}}}\exp \left(-ik{\frac {x^{2}}{2{q}_{x}(z)}}\right),\\u_{y}(y,z)&={\frac {1}{\sqrt {{q}_{y}(z)}}}\exp \left(-ik{\frac {y^{2}}{2{q}_{y}(z)}}\right),\end{aligned}}$$

где q _x ( z ) и q _y ( z ) — комплексные параметры луча в направлениях x и y .

Для общего случая круглого профиля балки q x ₍ z ) = q _y ( z ) = q ( z ) и x ² + и ² = р ² , что дает $$u(r,z)={\frac {1}{q(z)}}\exp \left(-ik{\frac {r^{2}}{2q(z)}}\right).$$

Лучевая оптика

Схема гауссова луча, проходящего через линзу.

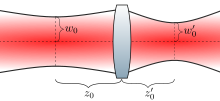
Когда гауссов луч распространяется через тонкую линзу , выходящий луч также является (другим) гауссовым лучом, при условии, что луч движется вдоль цилиндрической оси симметрии линзы и что линза больше ширины луча. Фокусное расстояние объектива $f$, радиус перетяжки балки $w_{0}$и положение талии пучка $z_{0}$ входящего луча можно использовать для определения радиуса перетяжки луча $w_{0}'$ и позиция $z_{0}'$ исходящего луча.

Уравнение линзы

Как установили Салех и Тейх, взаимосвязь между входящим и выходящим лучами можно найти, рассматривая фазу , которая добавляется к каждой точке. $(x,y)$ гауссова луча при прохождении через линзу. Альтернативный подход, предложенный Селфом, состоит в рассмотрении влияния тонкой линзы на волновые фронты гауссова луча .

Точное решение поставленной задачи выражается просто через увеличение. $M$

${\begin{aligned}w_{0}'&=Mw_{0}\\[1.2ex](z_{0}'-f)&=M^{2}(z_{0}-f).\end{aligned}}$

Увеличение, которое зависит от $w_{0}$ и $z_{0}$, определяется

$M={\frac {M_{r}}{\sqrt {1+r^{2}}}}$

где

$r={\frac {z_{R}}{z_{0}-f}},\quad M_{r}=\left|{\frac {f}{z_{0}-f}}\right|.$

Эквивалентное выражение для положения луча $z_{0}'$ является

${\frac {1}{z_{0}+{\frac {z_{R}^{2}}{(z_{0}-f)}}}}+{\frac {1}{z_{0}'}}={\frac {1}{f}}.$

Последнее выражение ясно показывает, что уравнение лучевой оптики тонкой линзы восстанавливается в пределе, когда $\left|\left({\tfrac {z_{R}}{z_{0}}}\right)\left({\tfrac {z_{R}}{z_{0}-f}}\right)\right|\ll 1$. Также можно отметить, что если $\left|z_{0}+{\frac {z_{R}^{2}}{z_{0}-f}}\right|\gg f$ тогда входящий луч «хорошо коллимирован», так что $z_{0}'\approx f$.

Фокусировка луча

В некоторых случаях желательно использовать собирающую линзу для фокусировки лазерного луча в очень маленькое пятно. Математически это означает минимизацию увеличения. $M$. Если размер луча ограничен размером доступной оптики, обычно этого лучше всего достичь, направляя максимально возможный коллимированный луч через линзу с малым фокусным расстоянием, т. е. максимизируя $z_{R}$ и минимизация $f$. В этой ситуации оправдано приближение $z_{R}^{2}/(z_{0}-f)^{2}\gg 1$, подразумевая, что $M\approx f/z_{R}$ и получение результата $w_{0}'\approx fw_{0}/z_{R}$. Этот результат часто представляют в виде

${\begin{aligned}2w_{0}'&\approx {\frac {4}{\pi }}\lambda F_{\#}\\[1.2ex]z_{0}'&\approx f\end{aligned}}$

где

$F_{\#}={\frac {f}{2w_{0}}},$

который находится после предположения, что среда имеет показатель преломления $n\approx 1$ и замена $z_{R}=\pi w_{0}^{2}/\lambda$. Коэффициент 2 вводится из-за общего предпочтения представлять размер балки диаметром перетяжки балки. $2w_{0}'$ и $2w_{0}$, а не радиусы талии $w_{0}'$ и $w_{0}$.

Волновое уравнение

Как частный случай электромагнитного излучения , гауссовы пучки (и гауссовы моды более высокого порядка, подробно описанные ниже) являются решениями волнового уравнения для электромагнитного поля в свободном пространстве или в однородной диэлектрической среде: получен путем объединения уравнений Максвелла для ротора E и ротора H , в результате чего: $$\nabla ^{2}U={\frac {1}{c^{2}}}{\frac {\partial ^{2}U}{\partial t^{2}}},$$где c — скорость света в среде , а U может относиться либо к вектору электрического, либо к вектору магнитного поля, поскольку любое конкретное решение для каждого из них определяет другое. Решение с гауссовым пучком справедливо только в параксиальном приближении, то есть когда распространение волны ограничено направлениями внутри небольшого угла оси. Без ограничения общности примем это направление как направление + z , и в этом случае решение U обычно можно записать через u , которое не зависит от времени и относительно плавно меняется в пространстве, при этом основное изменение пространственно соответствует волновому числу k в направлении z : $$U(x,y,z,t)=u(x,y,z)e^{-i(kz-\omega t)}\,{\hat {\mathbf {x} }}\,.$$

Используя эту форму вместе с параксиальным приближением, ∂ ² в /∂ z ² тогда можно по существу пренебречь. Поскольку решения уравнения электромагнитной волны справедливы только для поляризаций, ортогональных направлению распространения ( z ), мы без ограничения общности считали, что поляризация имеет направление x , так что теперь мы решаем скалярное уравнение для u ( x , y , z ) .

Подстановка этого решения в приведенное выше волновое уравнение дает параксиальное приближение скалярного волнового уравнения: $${\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}=2ik{\frac {\partial u}{\partial z}}.$$Запись волновых уравнений в координатах светового конуса возвращает это уравнение без использования какого-либо приближения. Гауссовы пучки с любой перетяжкой w ₀ удовлетворяют параксиальному приближению скалярного волнового уравнения; это легче всего проверить, выразив волну в точке z через комплексный параметр луча q ( z ), как определено выше. Есть много других решений. Как и решения линейной системы , любая комбинация решений (с помощью сложения или умножения на константу) также является решением. Фундаментальный гауссиан — это тот, который минимизирует произведение минимального размера пятна и дивергенции в дальней зоне, как отмечалось выше. При поиске параксиальных решений, в частности таких, которые описывали бы лазерное излучение, не находящееся в фундаментальной гауссовой моде, мы будем искать семейства решений с постепенно возрастающими произведениями их расходимостей и минимальными размерами пятна. Двумя важными ортогональными разложениями такого типа являются моды Эрмита-Гаусса или Лагерра-Гаусса, соответствующие прямоугольной и круговой симметрии соответственно, как подробно описано в следующем разделе. В обоих случаях рассматриваемый нами фундаментальный гауссов пучок является модой низшего порядка.

Режимы высшего порядка

См. также: Поперечный режим.

Режимы Эрмита-Гаусса

Двенадцать режимов Эрмита-Гаусса

Можно разложить когерентный параксиальный луч, используя ортогональный набор так называемых мод Эрмита-Гаусса , любая из которых задается произведением коэффициента x и коэффициента y . Такое решение возможно благодаря разделимости по x и y в параксиальном уравнении Гельмгольца , записанном в декартовых координатах . Таким образом, учитывая режим порядка ( l , m ), относящийся к направлениям x и y , амплитуда электрического поля в точках x , y , z может быть задана следующим образом: $$E(x,y,z)=u_{l}(x,z)\,u_{m}(y,z)\,\exp(-ikz),$$ где коэффициенты зависимости x и y определяются следующим образом: $$u_{J}(x,z)=\left({\frac {\sqrt {2/\pi }}{2^{J}\,J!\;w_{0}}}\right)^{\!\!1/2}\!\!\left({\frac {{q}_{0}}{{q}(z)}}\right)^{\!\!1/2}\!\!\left(-{\frac {{q}^{\ast }(z)}{{q}(z)}}\right)^{\!\!J/2}\!\!H_{J}\!\left({\frac {{\sqrt {2}}x}{w(z)}}\right)\,\exp \left(\!-i{\frac {kx^{2}}{2{q}(z)}}\right),$$где мы использовали комплексный параметр луча q ( z ) (как определено выше) для луча с перетяжкой w ₀ в точке z от фокуса. В этой форме первый множитель — это просто нормализующая константа, делающая набор u _J ортонормированным . Второй фактор — это дополнительная нормализация, зависящая от z , которая компенсирует расширение пространственной протяженности моды по w ( z )/ w ₀ (за счет двух последних факторов). Он также содержит часть фазы Гуи. Третий фактор — это чистая фаза, которая усиливает фазовый сдвиг Гуи для более высоких J. порядков

Последние два фактора объясняют пространственное изменение по x (или y ). Четвертым фактором является полином Эрмита порядка J («форма физики», т.е. H ₁ ( x ) = 2 x ), а пятый отвечает за гауссовское спад амплитуды exp(− x ² / ш ( z ) ² ) , хотя это не очевидно, если использовать комплекс q в показателе степени. Расширение этой экспоненты также дает фазовый коэффициент в x , который учитывает кривизну волнового фронта ( 1/ R ( z ) ) в точке z вдоль луча.

Режимы Эрмита-Гаусса обычно обозначаются «TEM _lm »; Таким образом, фундаментальный гауссов пучок можно назвать TEM ₀₀ (где TEM — поперечное электромагнитное излучение ). Умножив u _l ( x , z ) и um _, ( y , z ) чтобы получить профиль двумерного режима, и удалив нормализацию так, чтобы ведущий фактор назывался просто E ₀ , мы можем написать ( l , m ) режим в более доступной форме:

$${\begin{aligned}E_{l,m}(x,y,z)={}&E_{0}{\frac {w_{0}}{w(z)}}\,H_{l}\!{\Bigg (}{\frac {{\sqrt {2}}\,x}{w(z)}}{\Bigg )}\,H_{m}\!{\Bigg (}{\frac {{\sqrt {2}}\,y}{w(z)}}{\Bigg )}\times {}\\&\exp \left({-{\frac {x^{2}+y^{2}}{w^{2}(z)}}}\right)\exp \left({-i{\frac {k(x^{2}+y^{2})}{2R(z)}}}\right)\times {}\\&\exp {\big (}i\psi (z){\big )}\exp(-ikz).\end{aligned}}$$

В этой форме параметр w ₀ , как и прежде, определяет семейство мод, в частности, масштабирует пространственную протяженность перетяжки основной моды и всех других моделей мод при z = 0 . Учитывая, что w0 _{описанного} , w ( z ) и R ( z ) имеют те же определения, что и для фундаментального гауссова пучка, выше . Видно, что при l = m = 0 мы получаем описанный ранее фундаментальный гауссов пучок (поскольку H ₀ = 1 ). Единственная специфическая разница в профилях x и y при любом z связана с коэффициентами полинома Эрмита для порядковых номеров l и m . Однако есть изменение в эволюции фазы Гуи мод по z : $$\psi (z)=(N+1)\,\arctan \left({\frac {z}{z_{\mathrm {R} }}}\right),$$

где объединенный порядок моды N определяется как N = l + m . Хотя фазовый сдвиг Гуи для фундаментальной (0,0) гауссовской моды изменяется только на ± π /2 радиан по всем z (и только на ± π /4 радиан между ± z _R ), он увеличивается раз в 1 для мод высшего порядка.

Эрмитовые гауссовы моды с их прямоугольной симметрией особенно подходят для модального анализа излучения лазеров, конструкция резонатора которых асимметрична в прямоугольной форме. С другой стороны, с лазерами и системами с круговой симметрией лучше обращаться, используя набор мод Лагерра-Гаусса, представленный в следующем разделе.

Режимы Лагерра-Гаусса

Профили интенсивности первых 12 мод Лагерра-Гаусса.

Профили луча, имеющие круговую симметрию (или лазеры с цилиндрически-симметричными резонаторами), часто лучше всего решать с помощью модального разложения Лагерра-Гаусса. Эти функции записаны в цилиндрических координатах с использованием обобщенных полиномов Лагерра . Каждая поперечная мода снова помечается двумя целыми числами, в данном случае радиальным индексом p ≥ 0 и азимутальным индексом l, который может быть положительным или отрицательным (или нулевым):

Пучок Лагерра-Гаусса с l=1 и p=0

$${\begin{aligned}u(r,\phi ,z)={}&C_{lp}^{LG}{\frac {1}{w(z)}}\left({\frac {r{\sqrt {2}}}{w(z)}}\right)^{\!|l|}\exp \!\left(\!-{\frac {r^{2}}{w^{2}(z)}}\right)L_{p}^{|l|}\!\left({\frac {2r^{2}}{w^{2}(z)}}\right)\times {}\\&\exp \!\left(\!-ik{\frac {r^{2}}{2R(z)}}\right)\exp(-il\phi )\,\exp(i\psi (z)),\end{aligned}}$$

где L _п ^л являются обобщенными полиномами Лагерра . С ^LG
_lp — необходимая константа нормализации: $$C_{lp}^{LG}={\sqrt {\frac {2p!}{\pi (p+|l|)!}}}\Rightarrow \int _{0}^{2\pi }d\phi \int _{0}^{\infty }dr\;r\,|u(r,\phi ,z)|^{2}=1,$$.

w ( z ) и R ( z ) имеют те же определения, что и выше . Как и в случае с модами Эрмита-Гаусса более высокого порядка, величина фазового сдвига Гуи мод Лагерра-Гаусса преувеличена в коэффициент N + 1 : $$\psi (z)=(N+1)\,\arctan \left({\frac {z}{z_{\mathrm {R} }}}\right),$$где в этом случае комбинированный номер моды N = | л | + 2 п . Как и раньше, поперечные изменения амплитуды содержатся в последних двух факторах в верхней строке уравнения, которые снова включают в себя основное гауссовское падение r, но теперь умноженное на полином Лагерра. Влияние вращательной моды номера l , помимо влияния на полином Лагерра, в основном содержится в фазовом коэффициенте exp(− ilφ ) , при котором профиль луча опережает (или замедляет) на l полные 2 π фазы за один оборот. вокруг балки (в φ ). Это пример оптического вихря с топологическим зарядом l , который может быть связан с орбитальным угловым моментом света в этом режиме.

Инс-гауссовы режимы

Профиль поперечной амплитуды даже инце-гауссовских мод низшего порядка.

В эллиптических координатах можно записать моды более высокого порядка, используя полиномы Ince . Четные и нечетные режимы Ince-Gaussian задаются формулой

$$u_{\varepsilon }\left(\xi ,\eta ,z\right)={\frac {w_{0}}{w\left(z\right)}}\mathrm {C} _{p}^{m}\left(i\xi ,\varepsilon \right)\mathrm {C} _{p}^{m}\left(\eta ,\varepsilon \right)\exp \left[-ik{\frac {r^{2}}{2q\left(z\right)}}-\left(p+1\right)\zeta \left(z\right)\right],$$где ξ и η — радиальные и угловые эллиптические координаты, определяемые формулой $${\begin{aligned}x&={\sqrt {\varepsilon /2}}\;w(z)\cosh \xi \cos \eta ,\\y&={\sqrt {\varepsilon /2}}\;w(z)\sinh \xi \sin \eta .\end{aligned}}$$С ^м
_p ( η , ε ) — четные полиномы Ince порядка p и степени m , где ε — параметр эллиптичности. Режимы Эрмита-Гаусса и Лагерра-Гаусса являются частным случаем режимов Инса-Гаусса для ε = ∞ и ε = 0 соответственно.

Гипергеометрическо-гауссовы режимы

Существует еще один важный класс параксиальных волновых мод в цилиндрических координатах , в которых комплексная амплитуда пропорциональна вырожденной гипергеометрической функции .

Эти моды имеют сингулярный фазовый профиль и являются собственными функциями орбитального углового момента фотона . Их профили интенсивности характеризуются одним блестящим кольцом; как и моды Лагерра – Гаусса, их интенсивности падают до нуля в центре (на оптической оси), за исключением основной (0,0) моды. Комплексную амплитуду моды можно записать через нормированную (безразмерную) радиальную координату ρ = r / w ₀ и нормированную продольную координату Ζ = z / z _R следующим образом:

$${\begin{aligned}u_{{\mathsf {p}}m}(\rho ,\phi ,\mathrm {Z} ){}={}&{\sqrt {\frac {2^{{\mathsf {p}}+|m|+1}}{\pi \Gamma ({\mathsf {p}}+|m|+1)}}}\;{\frac {\Gamma \left({\frac {\mathsf {p}}{2}}+|m|+1\right)}{\Gamma (|m|+1)}}\,i^{|m|+1}\times {}\\&\mathrm {Z} ^{\frac {\mathsf {p}}{2}}\,(\mathrm {Z} +i)^{-\left({\frac {\mathsf {p}}{2}}+|m|+1\right)}\,\rho ^{|m|}\times {}\\&\exp \left(-{\frac {i\rho ^{2}}{\mathrm {Z} +i}}\right)\,e^{im\phi }\,{}_{1}F_{1}\left(-{\frac {\mathsf {p}}{2}},|m|+1;{\frac {\rho ^{2}}{\mathrm {Z} (\mathrm {Z} +i)}}\right)\end{aligned}}$$

где индекс вращения m является целым числом, и ${\mathsf {p}}\geq -|m|$ является вещественным, Γ( x ) является гамма-функцией и ₁ F ₁ ( a , b ; x ) является вырожденной гипергеометрической функцией.

Некоторые подсемейства гипергеометрическо-гауссовских режимов (HyGG) можно перечислить как модифицированные режимы Бесселя-Гаусса, модифицированные экспоненциальные гауссовы режимы, и модифицированные моды Лагерра – Гаусса.

Набор гипергеометрическо-гауссовских мод является сверхполным и не является ортогональным набором мод. Несмотря на сложный профиль поля, моды HyGG имеют очень простой профиль в перетяжке пучка ( z = 0 ): $$u(\rho ,\phi ,0)\propto \rho ^{{\mathsf {p}}+|m|}e^{-\rho ^{2}+im\phi }.$$

См. также

• Бессельская балка
• Топатная балка
• Профилометр лазерного луча
• Квазиоптика

Ссылки

• Бандрес, Мигель А.; Гутьеррес-Вега, Хулио К. (2004). «Инс-гауссовы лучи» . Опция Летт . 29 (2). ОСА: 144–146. Бибкод : 2004OptL...29..144B . дои : 10.1364/OL.29.000144 . ПМИД   14743992 .
• Гарг, Анупам (2012). Классический электромагнетизм в двух словах . Принстон, Нью-Джерси: Издательство Принстонского университета. ISBN  978-0691130187 .
• Губо, Г.; Шверинг, Ф. (1961). «О направленном распространении пучков электромагнитных волн». ИРЭ Транс . 9 (3): 248–256. Бибкод : 1961ITAP....9..248G . дои : 10.1109/TAP.1961.1144999 . МР   0134166 .
• Карими, Э.; Зито, Г.; Пиччирилло, Б.; Марруччи, Л.; Сантамато, Э. (2007). «Гипергеометрическо-гауссовы пучки» . Опция Летт . 32 (21). ОСА: 3053–3055. arXiv : 0712.0782 . Бибкод : 2007OptL...32.3053K . дои : 10.1364/OL.32.003053 . ПМИД   17975594 . S2CID   46526713 .
• Мандель, Леонард; Вольф, Эмиль (1995). Оптическая когерентность и квантовая оптика . Кембридж: Издательство Кембриджского университета. ISBN  0-521-41711-2 . Глава 5, «Оптические лучи», стр. 267.
• Пампалони, Ф.; Эндерляйн, Дж. (2004). «Гауссовы пучки, пучки Эрмита-Гаусса и Лагерра-Гаусса: введение». arXiv : физика/0410021 .
• Сакпал, С.; Милион, Г.; Ли, М.; Нури, М.; Шахоэй, Х.; ЛаФав, Т.; Ашрафи, С.; Макфарлейн, Д. (2018). «Стабильность инце-гауссовых пучков в маломодовых волокнах с эллиптической сердцевиной» . Опция Летт . 43 (11): 2656–2659. Бибкод : 2018OptL...43.2656S . дои : 10.1364/OL.43.002656 . ПМИД   29856389 . S2CID   46921059 .
• Салех, Восточная EA; Тейх, Малвин Карл (1991). Основы фотоники Нью-Йорк: Джон Уайли и сыновья. ISBN  0-471-83965-5 . Глава 3, «Лучевая оптика», стр. 80–107.
• Зигман, Энтони Э. (1986). Лазеры . Университетские научные книги. ISBN  0-935702-11-3 . Глава 16.
• Свелто, Орацио (2010). Принципы лазеров (5-е изд.).
• Ярив, Амнон (1989). Квантовая электроника (3-е изд.). Уайли. ISBN  0-471-60997-8 .

Внешние ссылки

• Учебное пособие по гауссовой лучевой оптике, Ньюпорт