Заблуждения о нормальном распределении

У студентов, изучающих статистику и теорию вероятностей, иногда возникают неверные представления о нормальном распределении, идеи, которые могут показаться правдоподобными, но математически неверны. Например, иногда ошибочно полагают, что две линейно некоррелированные , нормально распределенные случайные величины должны быть статистически независимыми . Однако это неверно, как можно доказать на контрпримере. Точно так же иногда ошибочно полагают, что линейная комбинация нормально распределенных случайных величин сама по себе будет нормально распределенной, но опять же контрпримеры доказывают это неправильно. ^[1]^[2]

Сказать, что пара $(X,Y)$ случайных величин имеет двумерное нормальное распределение, что означает, что каждая линейная комбинация $aX+bY$ из $X$ и $Y$ для постоянных (т.е. неслучайных) коэффициентов $a$ и $b$ (не оба равны нулю) имеет одномерное нормальное распределение. В том случае, если $X$ и $Y$ некоррелированы, то они независимы. ^[3] Однако возможно и для двух случайных величин $X$ и $Y$ быть настолько распределены совместно, что каждый из них в отдельности распределен незначительно нормально, и они некоррелированы, но не независимы; примеры приведены ниже.

Примеры

Симметричный пример

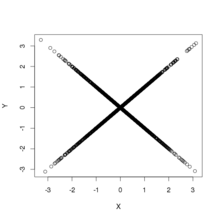
Предполагать $X$ имеет нормальное распределение с ожидаемым значением 0 и дисперсией 1. Пусть $W$ имеют распределение Радемахера , так что $W=1$ или $W=-1$ , каждый с вероятностью 1/2, и предположим $W$ не зависит от $X$ . Позволять $Y=WX$ . Затем $X$ и $Y$ некоррелированы, в чем можно убедиться, вычислив их ковариацию . Более того, оба имеют одинаковое нормальное распределение. И все же, $X$ и $Y$ не являются независимыми. ^[4]^[1]^[5]

Чтобы увидеть это $X$ и $Y$ не являются независимыми, заметим, что $|Y|=|X|$ или что $\operatorname {Pr} (Y>1|-1/2<X<1/2)=\operatorname {Pr} (X>1|-1/2<X<1/2)=0$ .

Наконец, распределение простой линейной комбинации $X+Y$ концентрирует положительную вероятность в 0: $\operatorname {Pr} (X+Y=0)=1/2$ . Следовательно, случайная величина $X+Y$ не является нормально распределенным, и поэтому также $X$ и $Y$ не являются совместно нормально распределенными (согласно приведенному выше определению). ^[4]

Асимметричный пример

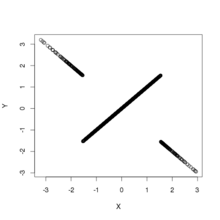
Предполагать $X$ имеет нормальное распределение с ожидаемым значением 0 и дисперсией 1. Пусть $Y=\left\{{\begin{matrix}X&{\text{if }}\left|X\right|\leq c\\-X&{\text{if }}\left|X\right|>c\end{matrix}}\right.$ где $c$ – положительное число, которое будет указано ниже. Если $c$ очень мала, то корреляция $\operatorname {corr} (X,Y)$ рядом $-1$ если $c$ очень велико, то $\operatorname {corr} (X,Y)$ близко к 1. Поскольку корреляция является непрерывной функцией $c$ , теорема о промежуточном значении подразумевает, что существует некоторое конкретное значение $c$ это делает корреляцию равной 0. Это значение составляет примерно 1,54. ^[2]^{[примечание 1]} В этом случае $X$ и $Y$ некоррелированы, но явно не независимы, поскольку $X$ полностью определяет $Y$ .

Чтобы увидеть это $Y$ нормально распределена — более того, ее распределение такое же, как и у $X$ — можно вычислить его кумулятивную функцию распределения : ^[6] ${\begin{aligned}\Pr(Y\leq x)&=\Pr(\{|X|\leq c{\text{ and }}X\leq x\}{\text{ or }}\{|X|>c{\text{ and }}-X\leq x\})\\&=\Pr(|X|\leq c{\text{ and }}X\leq x)+\Pr(|X|>c{\text{ and }}-X\leq x)\\&=\Pr(|X|\leq c{\text{ and }}X\leq x)+\Pr(|X|>c{\text{ and }}X\leq x)\\&=\Pr(X\leq x),\end{aligned}}$

где предпоследнее равенство следует из симметричности распределения $X$ и симметрия условия, что $|X|\leq c$ .

В этом примере разница $X-Y$ далеко не является нормально распределенным, поскольку существует значительная вероятность (около 0,88) того, что оно будет равно 0. Напротив, нормальное распределение, будучи непрерывным распределением, не имеет дискретной части, то есть оно не концентрирует более нулевая вероятность в любой отдельной точке. Следовательно $X$ и $Y$ не являются совместно нормально распределенными, хотя они нормально распределены отдельно. ^[2]

Примеры с поддержкой практически везде в плоскости

Предположим, что координаты $(X,Y)$ случайной точки на плоскости выбираются в соответствии с функцией плотности вероятности $p(x,y)={\frac {1}{2\pi {\sqrt {3}}}}\left[\exp \left(-{\frac {2}{3}}(x^{2}+xy+y^{2})\right)+\exp \left(-{\frac {2}{3}}(x^{2}-xy+y^{2})\right)\right].$ Тогда случайные величины $X$ и $Y$ некоррелированы, и каждый из них имеет нормальное распределение (со средним значением 0 и дисперсией 1), но они не являются независимыми. ^[7]^: 93

Известно, что соотношение $C$ двух независимых стандартных нормальных случайных отклонений $X_{i}$ и $Y_{i}$ имеет распределение Коши . ^[8]^[9]^[7]^: 122 С таким же успехом можно начать со случайной величины Коши $C$ и выведем условное распределение $Y_{i}$ удовлетворить требование о том, что $X_{i}=CY_{i}$ с $X_{i}$ и $Y_{i}$ независимый и стандартный нормальный. Отсюда следует, что $Y_{i}=W_{i}{\sqrt {\frac {\chi _{i}^{2}\left(k=2\right)}{1+C^{2}}}}$ в котором $W_{i}$ является случайной величиной Радемахера и $\chi _{i}^{2}\left(k=2\right)$ — случайная величина хи-квадрат с двумя степенями свободы.

Рассмотрим два набора $\left(X_{i},Y_{i}\right)$ , $i\in \left\{1,2\right\}$ . Обратите внимание, что $C$ не индексируется $i$ – то есть та же случайная величина Коши $C$ используется в определении обоих $\left(X_{1},Y_{1}\right)$ и $\left(X_{2},Y_{2}\right)$ . Это разделение $C$ приводит к зависимости между индексами: ни $X_{1}$ ни $Y_{1}$ не зависит от $Y_{2}$ . Тем не менее все $X_{i}$ и $Y_{i}$ некоррелированы, поскольку все двумерные распределения обладают симметрией отражения по осям. ^{[ нужна ссылка ]}

На рисунке показаны диаграммы рассеяния выборок, взятых из приведенного выше распределения. Это дает два примера двумерных распределений, которые не коррелируют и имеют нормальные маргинальные распределения, но не являются независимыми. На левой панели показано совместное распределение $X_{1}$ и $Y_{2}$ ; дистрибутив имеет поддержку везде, кроме источника. На правой панели показано совместное распределение $Y_{1}$ и $Y_{2}$ ; распределение имеет поддержку везде, кроме вдоль осей, и имеет разрыв в начале координат: плотность расходится при приближении к началу координат по любому прямому пути, кроме вдоль осей.

См. также

Корреляция и зависимость

Ссылки

^ Jump up to: ^а ^б Розенталь, Джеффри С. (2005). «Разглагольствования о некоррелированных нормальных случайных величинах» .
^ Jump up to: ^а ^б ^с Мельник, Эдвард Л.; Тененбейн, Аарон (ноябрь 1982 г.). «Неверные спецификации нормального распределения». Американский статистик . 36 (4): 372–373. дои : 10.1080/00031305.1982.10483052 .
^ Хогг, Роберт ; Танис, Эллиот (2001). «Глава 5.4 Двумерное нормальное распределение». Вероятность и статистический вывод (6-е изд.). Прентис Холл. стр. 258–259. ISBN 0130272949 .
^ Jump up to: ^а ^б Эш, Роберт Б. «Лекция 21. Многомерное нормальное распределение » (PDF) . Лекции по статистике . Архивировано из оригинала (PDF) 14 июля 2007 г.
^ Романо, Джозеф П.; Сигел, Эндрю Ф. (1986). Контрпримеры в теории вероятности и статистике . Уодсворт и Брукс/Коул. стр. 65–66. ISBN 0-534-05568-0 .
^ Уайз, Гэри Л.; Холл, Эрик Б. (1993). Контрпримеры в теории вероятности и реальном анализе . Издательство Оксфордского университета. стр. 140–141. ISBN 0-19-507068-2 .
^ Jump up to: ^а ^б Стоянов, Джордан М. (2013). Контрпримеры в теории вероятности (3-е изд.). Дувр. ISBN 978-0-486-49998-7 .
^ Патель, Джагдиш К.; Прочтите, Кэмпбелл Б. (1996). Справочник по нормальному распределению (2-е изд.). Тейлор и Фрэнсис. п. 113. ИСБН 978-0-824-79342-5 .
^ Кришнамурти, К. (2006). Справочник по статистическим распределениям с приложениями . ЦРК Пресс. п. 278. ИСБН 978-1-420-01137-1 .

Примечания

^ Точнее, 1,53817..., квадратный корень из медианы распределения хи-квадрат с 3 степенями свободы.

[Rosenthal-1] Jump up to: ^а ^б Розенталь, Джеффри С. (2005). «Разглагольствования о некоррелированных нормальных случайных величинах» .

[Melnick1982-2] Jump up to: ^а ^б ^с Мельник, Эдвард Л.; Тененбейн, Аарон (ноябрь 1982 г.). «Неверные спецификации нормального распределения». Американский статистик . 36 (4): 372–373. дои : 10.1080/00031305.1982.10483052 .

[3] Хогг, Роберт ; Танис, Эллиот (2001). «Глава 5.4 Двумерное нормальное распределение». Вероятность и статистический вывод (6-е изд.). Прентис Холл. стр. 258–259. ISBN 0130272949 .

[Ash-4] Jump up to: ^а ^б Эш, Роберт Б. «Лекция 21. Многомерное нормальное распределение » (PDF) . Лекции по статистике . Архивировано из оригинала (PDF) 14 июля 2007 г.

[5] Романо, Джозеф П.; Сигел, Эндрю Ф. (1986). Контрпримеры в теории вероятности и статистике . Уодсворт и Брукс/Коул. стр. 65–66. ISBN 0-534-05568-0 .

[7] Уайз, Гэри Л.; Холл, Эрик Б. (1993). Контрпримеры в теории вероятности и реальном анализе . Издательство Оксфордского университета. стр. 140–141. ISBN 0-19-507068-2 .

[Stoyanov-8] Jump up to: ^а ^б Стоянов, Джордан М. (2013). Контрпримеры в теории вероятности (3-е изд.). Дувр. ISBN 978-0-486-49998-7 .

[9] Патель, Джагдиш К.; Прочтите, Кэмпбелл Б. (1996). Справочник по нормальному распределению (2-е изд.). Тейлор и Фрэнсис. п. 113. ИСБН 978-0-824-79342-5 .

[10] Кришнамурти, К. (2006). Справочник по статистическим распределениям с приложениями . ЦРК Пресс. п. 278. ИСБН 978-1-420-01137-1 .

[6] Точнее, 1,53817..., квадратный корень из медианы распределения хи-квадрат с 3 степенями свободы.

[1]

[2]

[3]

[4]

[5]

[примечание 1]

[6]

[7]

[8]

[9]