Треугольник площадью одна седьмая

В плоской геометрии треугольник ABC содержит треугольник, имеющий одну седьмую площади ABC , который образуется следующим образом: стороны этого треугольника лежат на чевианах p, q, r , где

p соединяет A с точкой на BC , которая находится на одну треть расстояния от B до C ,

q соединяет B с точкой на CA , которая находится на одной трети расстояния от C до A ,

r соединяет C с точкой на AB которая находится на одной трети расстояния от A до B. ,

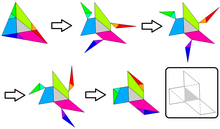
Доказательство существования треугольника площади одной седьмой следует из построения шести параллельных прямых:

два параллельно p , один через C , другой через qr

два параллельно q , один через A , другой через rp

два параллельны r , один через B , другой через pq .

Предложение Хьюго Штейнхауса состоит в том, чтобы (центральный) треугольник со сторонами p,q,r отражался в своих сторонах и вершинах. ^[1] Эти шесть дополнительных треугольников частично покрывают ABC и оставляют шесть нависающих дополнительных треугольников, лежащих за пределами ABC . Если обратить внимание на параллелизм всей конструкции (предложенной Мартином Гарднером через интернет-журнал Джеймса Рэнди ), становится очевидным парное совпадение нависающих и недостающих частей ABC . Как видно из графического решения, шесть плюс оригинал равняется целому треугольнику ABC . ^[2]

Графическое решение задачи о треугольнике площади одной седьмой. — Совпадение длин ребер позволяет вращать выбранные треугольники с образованием трех параллелограммов равной площади, которые делятся пополам на шесть треугольников одинакового размера с исходным внутренним треугольником.

Раннее описание этой геометрической конструкции и вычисления площади было дано Робертом Поттсом в 1859 году в его учебнике евклидовой геометрии. ^[3]

По словам Кука и Вуда (2004), этот треугольник озадачил Ричарда Фейнмана в разговоре за ужином; они приводят четыре разных доказательства. ^[4]

Более общий результат известен как теорема Рауса .

Ссылки

^ Хьюго Штайнхаус (1960) Математические снимки
^ Джеймс Рэнди (2001) Этот нарисованный треугольник , доказательство Мартина Гарднера
^ Роберт Поттс (1859) «Элементы геометрии Евклида» , пятое школьное издание, задачи 59 и 100, страницы 78 и 80, через Интернет-архив
^ Р. Дж. Кук и Г. Вуд (2004) «Треугольник Фейнмана», Mathematical Gazette 88: 299–302

HSM Coxeter (1969) «Введение в геометрию» , стр. 211, John Wiley & Sons .

[1] Хьюго Штайнхаус (1960) Математические снимки

[2] Джеймс Рэнди (2001) Этот нарисованный треугольник , доказательство Мартина Гарднера

[3] Роберт Поттс (1859) «Элементы геометрии Евклида» , пятое школьное издание, задачи 59 и 100, страницы 78 и 80, через Интернет-архив

[4] Р. Дж. Кук и Г. Вуд (2004) «Треугольник Фейнмана», Mathematical Gazette 88: 299–302

[1]

[2]

[3]

[4]