Закон распределения между монадами

В теории категорий , абстрактной отрасли математики , законы распределения между монадами — это способ абстрактно выразить то, что две алгебраические структуры распределяют друг друга.

Предположим, что $(S,\mu ^{S},\eta ^{S})$ и $(T,\mu ^{T},\eta ^{T})$ две категории C. монады нет естественной монадной структуры В общем, на составном функторе ST . существует естественная монадная структура, Однако на функторе ST существует закон распределения монады S над монадой T. если

Формально дистрибутивный закон монады S над монадой T представляет собой естественное преобразование

$l:TS\to ST$

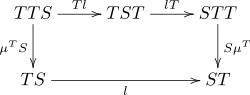
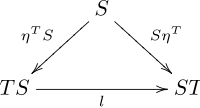
такие, что диаграммы

        

        

добираться .

Этот закон индуцирует составную монаду ST с

• как умножение: $STST{\xrightarrow {SlT}}SSTT{\xrightarrow {\mu ^{S}\mu ^{T}}}ST$,
• как единица: $1{\xrightarrow {\eta ^{S}\eta ^{T}}}ST$.

См. также

• Распределительная собственность

Ссылки

• Бек, Джон (1969). «Распределительные законы». Семинар по тройкам и теории категориальной гомологии, ETH 1966/67 . Конспект лекций по математике. Том. 80. стр. 119–140. дои : 10.1007/BFb0083084 . ISBN  978-3-540-04601-1 .

• Барр, Майкл ; Уэллс, Чарльз (1985). Топосы, тройки и теории (PDF) . Спрингер-Верлаг . ISBN  0-387-96115-1 . Архивировано из оригинала (PDF) 14 мая 2011 г.
• Распределительный закон в n Lab
• Бём, Г. (2005). «Внутренние биальгеброиды, переплетающиеся структуры и сердцевины». Алгебраические структуры и их представления . Современная математика. Том. 376. стр. 207–226. arXiv : math.QA/0311244 . ISBN  9780821836309 .
• Бжезинский, Т.; Маджид, С. (1998). «Расслоения коалгебры». Комм. Математика. Физ . 191 (2): 467–492. arXiv : q-alg/9602022 . Бибкод : 1998CMaPh.191..467B . дои : 10.1007/s002200050274 . S2CID   189829500 .
• Бжезинский, Томаш; Висбауэр, Роберт (2003). Коринги и комодулы . Серия лекций Лондонского математического общества. Том. 309. Издательство Кембриджского университета. ISBN  978-0-521-53931-9 .
• Фокс, ТФ; Маркл, М. (1997). «Дистрибутивные законы, биалгебры и когомологии». Операды: материалы конференций эпохи Возрождения . Современная математика. Том. 202. Американское математическое общество. стр. 167–205. ISBN  9780821805138 .
• Лак, С. (2004). «Составление реквизита» . Теория Прикл. Катег . 13 (9): 147–163.
• Лак, С.; Стрит, Р. (2002). «Формальная теория монад II». J. Pure Appl. Алгебра . 175 (1–3): 243–265. дои : 10.1016/S0022-4049(02)00137-8 .
• Маркл, М. (1996). «Распределительные законы и Кошульность» . Анналы Института Фурье . 46 (2): 307–323. arXiv : hep-th/9409192 . дои : 10.5802/aif.1516 . Збл   0853.18005 .
• Стрит, Р. (1972). «Формальная теория монад». J. Pure Appl. Алг . 2 (2): 149–168. дои : 10.1016/0022-4049(72)90019-9 .
• Шкода, З. (2004). «Распределительные законы для моноидальных категорий». arXiv : математика/0406310 .
• — (2007). «Эквивариантные монады и эквивариантные лифты против 2-категории распределительных законов». arXiv : 0707.1609 [ math.CT ].
• - (2008). «Бикатегория переплетений». arXiv : 0805.4611 [ math.RA ].
• - (2009). «Некоторые эквивариантные конструкции в некоммутативной геометрии». Грузинская математика. Дж . 16 (1): 183–202. arXiv : 0811.4770 . дои : 10.1515/GMJ.2009.183 . S2CID   121946556 .
• Висбауэр, Р. (2008). «Алгебры против коалгебр». Прил. Катег. Структуры . 16 (1–2): 255–295. дои : 10.1007/s10485-007-9076-5 . S2CID   8150337 .