Тест горизонтальной линии

В математике тест на горизонтальную линию — это тест, используемый для определения того, ли функция является инъективной (т. е. взаимно однозначной). ^[1]

В исчислении [ править ]

Горизонтальная линия — это прямая плоская линия, идущая слева направо. Дана функция $f\colon \mathbb {R} \to \mathbb {R}$ (т. е. от действительных чисел к действительным числам), мы можем решить, является ли она инъективной функции , глядя на горизонтальные линии, пересекающие график . Если какая-либо горизонтальная линия $y=c$ пересекает график более чем в одной точке, функция не инъективна. Чтобы убедиться в этом, обратите внимание, что точки пересечения имеют одинаковое значение y (поскольку они лежат на линии $y=c$ ), но разные значения x, что по определению означает, что функция не может быть инъективной. ^[1]

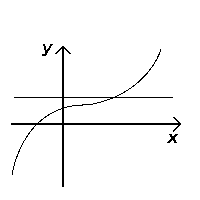Проходит тест (инъекционный)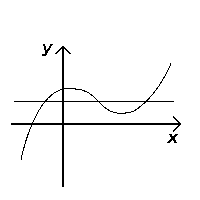

Не прошел тест (не инъекционный)

Варианты теста горизонтальной линии можно использовать, чтобы определить, является ли функция сюръективной или биективной :

Функция f является сюръективной (т.е. находящейся) тогда и только тогда, когда один раз пересекает любую горизонтальную линию ее график хотя бы .
f является биективным тогда и только тогда, когда любая горизонтальная линия пересекает график ровно один раз.

В теории множеств [ править ]

Рассмотрим функцию $f\colon X\to Y$ с соответствующим графиком как подмножеством декартова произведения $X\times Y$ . Рассмотрим горизонтальные линии в $X\times Y$ : $\{(x,y_{0})\in X\times Y:y_{0}{\text{ is constant}}\}=X\times \{y_{0}\}$ . Функция f инъективна . тогда и только тогда, когда каждая горизонтальная линия пересекает график не более одного раза В этом случае говорят, что график прошел тест на горизонтальную линию. Если какая-либо горизонтальная линия пересекает график более одного раза, функция не проходит тест на горизонтальную линию и не является инъективной. ^[2]

См. также [ править ]

Ссылки [ править ]

↑ Перейти обратно: Перейти обратно: ^а ^б Стюарт, Джеймс (2003). Исчисление с одной переменной: ранние трансценденталии (5-е изд.). Торонто, ON: Брук/Коул. стр. 64 . ISBN 0-534-39330-6 . Проверено 15 июля 2012 г. Таким образом, мы имеем следующий геометрический метод определения взаимно однозначности функции.
^ Цорн, Пол; Остеби, Арнольд (2002). Исчисление с графической, числовой и символической точек зрения (2-е изд.). Австралия: Брукс/Коул/Томсон Лиринг. п. 185. ИСБН 0-03-025681-Х . Ни одна горизонтальная линия не пересекает f-график более одного раза.

[Stewart-1] Перейти обратно: Перейти обратно: ^а ^б Стюарт, Джеймс (2003). Исчисление с одной переменной: ранние трансценденталии (5-е изд.). Торонто, ON: Брук/Коул. стр. 64 . ISBN 0-534-39330-6 . Проверено 15 июля 2012 г. Таким образом, мы имеем следующий геометрический метод определения взаимно однозначности функции.

[2] Цорн, Пол; Остеби, Арнольд (2002). Исчисление с графической, числовой и символической точек зрения (2-е изд.). Австралия: Брукс/Коул/Томсон Лиринг. п. 185. ИСБН 0-03-025681-Х . Ни одна горизонтальная линия не пересекает f-график более одного раза.

[1]

[2]