Реактор непрерывного действия с мешалкой

Схема, показывающая установку реактора непрерывного действия с мешалкой

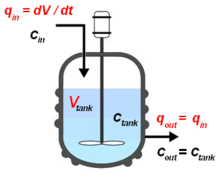
Реактор действия с мешалкой ( CSTR ), также известный как с чановым или реактор обратным смешением , реактор смешанного потока ( MFR ) или непрерывного потока реактор с мешалкой ( CF непрерывного STR ), является распространенной моделью химического реактора в химическая инженерия и экологическая инженерия . CSTR часто относится к модели, используемой для оценки ключевых переменных работы агрегата при использовании реактора непрерывного действия с перемешиванием для достижения заданной производительности. Математическая модель работает для всех жидкостей: жидкостей, газов и суспензий .

Поведение CSTR часто аппроксимируется или моделируется поведением идеального CSTR, предполагающего идеальное перемешивание . В реакторе с идеальным перемешиванием реагент мгновенно и равномерно перемешивается по всему реактору при входе. Следовательно, состав на выходе идентичен составу материала внутри реактора, который зависит от времени пребывания и скорости реакции. CSTR является идеальным пределом полного смешивания в конструкции реактора, который является полной противоположностью реактора идеального вытеснения (PFR). На практике ни один реактор не ведет себя идеально, а находится где-то между пределами смешивания идеальных CSTR и PFR.

Идеальный CSTR

Схема поперечного сечения CSTR

Моделирование

Непрерывный поток жидкости, содержащий неконсервативный химический реагент A, в идеальный CSTR объемом V. входит

Предположения:

• идеальное или идеальное смешивание
• устойчивое состояние ${\Bigl (}{\frac {dN_{A}}{dt}}=0{\Bigr )}$, где N _A – количество молей вида A
• закрытые границы
• жидкости постоянная плотность (действительно для большинства жидкостей; справедливо для газов только в том случае, если нет общего изменения количества молей или резкого изменения температуры)
• н ^й -реакция порядка ( r = kC _A ^н ), где k — константа скорости реакции, CA _— концентрация частиц A, n — порядок реакции
• изотермические условия, или постоянная температура ( k постоянна)
• единственная необратимая реакция ( ν _A = −1)
• Весь реагент А превращается в продукты посредством химической реакции.
• Н _А = С _А В

Интегральный баланс массы по числу молей N _A вида A в реакторе объемом V : $1.[{\text{Net accumulation of}}~A]=[A~{\text{in}}]-[A~{\text{out}}]+[{\text{Net generation of}}~A]$

$2.{\frac {dN_{A}}{dt}}=F_{Ao}-F_{A}+V\nu _{A}r_{A}$

где,

• F _Ao — молярный расход на входе вещества A.
• F _A — молярный расход на выходе вещества A.
• v _A – стехиометрический коэффициент
• r _A – скорость реакции

Применяя предположения об устойчивом состоянии и ν _A = −1, уравнение 2 упрощается до:

$3.\ 0=F_{Ao}-F_{A}-Vr_{A}$

Молярные скорости потока частиц A затем можно переписать через концентрацию A и скорость потока жидкости ( Q ):

$4.\ 0=QC_{Ao}-QC_{A}-Vr_{A}$

Уравнение 4 затем можно перестроить, чтобы изолировать r _A и упростить:

$5.\ r_{A}={\frac {Q}{V}}(C_{Ao}-C_{A})$

$6.\ r_{A}={\frac {1}{\tau }}(C_{Ao}-C_{A})$

где,

• $\tau$ – теоретическое время пребывания ( $\tau ={\tfrac {V}{Q}}$)
• C _Ao — входная концентрация частиц A
• CA _— концентрация вещества A в реакторе/на выходе.

Время пребывания — это общее количество времени, которое дискретное количество реагента проводит внутри реактора. Для идеального реактора теоретическое время пребывания $\tau$, всегда равен объему реактора, деленному на расход жидкости. См. следующий раздел для более подробного обсуждения распределения времени пребывания CSTR.

В зависимости от порядка реакции скорость реакции r _A обычно зависит от концентрации соединения A в реакторе и константы скорости. Ключевым допущением при моделировании CSTR является то, что любой реагент в жидкости идеально (т.е. равномерно) смешивается в реакторе, а это означает, что концентрация внутри реактора одинакова в выходном потоке. Константу скорости можно определить, используя известную эмпирическую скорость реакции, которая скорректирована с учетом температуры с помощью температурной зависимости Аррениуса . Обычно с повышением температуры увеличивается и скорость протекания реакции.

Уравнение 6 можно решить путем интегрирования после подстановки правильного выражения скорости. В таблице ниже приведены концентрации веществ А на выходе для идеального CSTR. Значения концентрации на выходе и времени пребывания являются основными критериями проектирования CSTR для промышленного применения.

Концентрация на выходе для идеального CSTR

Порядок реакции	С А
п=0	$C_{A}={C_{Ao}}-{k\tau }$
п=1	$C_{A}={\frac {C_{Ao}}{1+k\tau }}$
п=2	$C_{A}={\frac {-1+{\sqrt {1+4k\tau C_{Ao}}}}{2k\tau }}$
Другое н	Требуется численное решение

Распределение времени пребывания

Распределение возраста выхода E(t) и кумулятивное распределение возраста F(t) функции для идеального CSTR

в реакторе Идеальный CSTR будет демонстрировать четко определенное поведение потока, которое можно охарактеризовать распределением времени пребывания или распределением времени на выходе. Не все частицы жидкости будут проводить в реакторе одинаковое количество времени. Распределение возраста выхода (E(t)) определяет вероятность того, что данная частица жидкости проведет время t в реакторе. Аналогичным образом, кумулятивное распределение возраста (F(t)) дает вероятность того, что данная частица жидкости имеет возраст выхода меньше времени t. Одним из ключевых выводов из распределения возраста выхода является то, что очень небольшое количество частиц жидкости никогда не покинет CSTR. В зависимости от применения реактора это может быть либо преимуществом, либо недостатком.

Неидеальный CSTR

Хотя идеальная модель CSTR полезна для прогнозирования судьбы компонентов во время химического или биологического процесса, CSTR редко демонстрируют идеальное поведение в реальности. Чаще всего гидравлика реактора не ведет себя идеально или условия системы не подчиняются первоначальным предположениям. Идеальное смешивание — это теоретическая концепция, недостижимая на практике. Однако для инженерных целей, если время пребывания в 5–10 раз превышает время смешивания, предположение об идеальном смешивании обычно справедливо.

Распределение возраста выхода E(t) и кумулятивное распределение возраста F(t) функции для CSTR с мертвым пространством

Неидеальное поведение гидравлики обычно классифицируется как мертвое пространство или короткое замыкание. Эти явления возникают, когда какая-то жидкость проводит в реакторе меньше времени, чем теоретическое время пребывания. $\tau$. Наличие углов или перегородок в реакторе часто приводит к образованию мертвого пространства, в котором жидкость плохо перемешивается. Точно так же струя жидкости в реакторе может вызвать короткое замыкание, при котором часть потока выходит из реактора гораздо быстрее, чем основная масса жидкости. Если в CSTR возникает мертвое пространство или короткое замыкание, соответствующие химические или биологические реакции могут не завершиться до того, как жидкость выйдет из реактора. Любое отклонение от идеального потока приведет к тому, что распределение времени пребывания будет отличаться от идеального, как показано справа.

Моделирование неидеального потока

Хотя реакторы идеального потока редко встречаются на практике, они являются полезными инструментами для моделирования реакторов неидеального потока. Любой режим течения может быть достигнут путем моделирования реактора как комбинации идеальных CSTR и реакторов идеального вытеснения (PFR), соединенных последовательно или параллельно. Например, бесконечная серия идеальных CSTR гидравлически эквивалентна идеальному PFR. Модели реакторов, объединяющие несколько последовательно соединенных CSTR, часто называют моделями «резервуары в серии» (TIS).

Для моделирования систем, которые не подчиняются предположениям о постоянной температуре и единственной реакции, необходимо учитывать дополнительные зависимые переменные. Если система считается находящейся в нестационарном состоянии, необходимо решить дифференциальное уравнение или систему связанных дифференциальных уравнений. Отклонения в поведении CSTR можно учесть с помощью дисперсионной модели. Известно, что CSTR являются одной из систем, демонстрирующих сложное поведение, такое как стационарная множественность, предельные циклы и хаос.

Каскады CSTR

Серия из трех CSTR

Каскады CSTR, также известные как серии CSTR, используются для уменьшения объема системы.

Минимизация громкости

По мере увеличения количества последовательно соединенных CSTR общий объем реактора уменьшается.

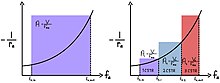
Как видно на графике с одним CSTR, где обратная ставка отображается как функция дробного преобразования , площадь в поле равна ${\frac {V}{F_{Ao}}}$ где V – общий объем реактора и $F_{Ao}$ – молярная скорость потока сырья. Когда тот же процесс применяется к каскаду CSTR, как показано на графике с тремя CSTR, объем каждого реактора рассчитывается на основе каждой дробной конверсии на входе и выходе, что приводит к уменьшению общего объема реактора. Оптимальный размер достигается, когда площадь над прямоугольниками последовательных CSTR, которая ранее покрывалась одним CSTR, максимизируется. Для реакции первого порядка с двумя CSTR следует использовать равные объемы. Поскольку количество идеальных CSTR (n) приближается к бесконечности, общий объем реактора приближается к идеальному PFR для той же реакции и фракционной конверсии.

CSTR

Из уравнения проектирования одного CSTR, где $\tau ={\frac {C_{Ao}-C_{A}}{-r_{A}}}$, мы можем определить, что для одного последовательного CSTR это $\tau _{i}={\frac {C_{A(i-1)}-C_{Ai}}{-r_{Ai}}}$

где $\tau$ - пространство-время реактора, $C_{Ao}$ - концентрация A в корме, $C_{A}$ - выходная концентрация A, и $-r_{A}$ это скорость реакции А.

Первый заказ

Для изотермической реакции первого порядка с постоянной плотностью в каскаде идентичных CSTR, работающих в установившемся режиме.

Для одного CSTR: $C_{A1}={\frac {C_{Ao}}{1+k\tau }}$, где k — константа скорости и $C_{A1}$ - концентрация A на выходе из первого CSTR

Два CSTR: $C_{A1}={\frac {C_{Ao}}{1+k\tau }}$ и $C_{A2}={\frac {C_{A1}}{1+k\tau }}$

Подключаем первое уравнение CSTR ко второму: $C_{A2}={\frac {C_{Ao}}{(1+k\tau )^{2}}}$

Следовательно, для m одинаковых последовательно соединенных CSTR: $C_{Am}={\frac {C_{Ao}}{(1+k\tau )^{m}}}$

Когда объемы отдельных последовательно расположенных CSTR изменяются, порядок CSTR не меняет общую конверсию реакции первого порядка, пока CSTR работают при одной и той же температуре.

Нулевой порядок

В установившемся состоянии общее уравнение изотермической реакции нулевого порядка в каскаде CSTR имеет вид $C_{Am}=C_{Ao}-\sum _{i=1}^{m}k_{i}\tau _{i}$

Когда каскад CSTR изотермичен с идентичными реакторами, концентрация определяется выражением $C_{Am}=C_{Ao}-mk_{i}\tau _{i}$

Второй заказ

Для изотермической реакции второго порядка в установившемся состоянии в каскаде CSTR общее уравнение расчета: $C_{Ai}={\frac {-1+{\sqrt {1+4k_{i}\tau _{i}C_{A(i-1)}}}}{2k_{i}\tau _{i}}}$

Неидеальный каскад CSTR

Для неидеальных реакторов распределение времени пребывания можно рассчитать . При концентрации в j-м последовательном реакторе определяется выражением

${\frac {C_{j}}{C_{o}}}=1-e^{-{\frac {nt}{\bar {t}}}}[1+{\frac {nt}{\bar {t}}}+{\frac {1}{2!}}({\frac {nt}{\bar {t}}})^{2}+...+{\frac {1}{(j-1)!}}({\frac {nt}{\bar {t}}})^{j-1}]$

где n — общее количество последовательных CSTR, а ${\bar {t}}$ среднее время пребывания каскада, определяемое формулой ${\bar {t}}={\frac {V}{Q}}$ где Q — объемный расход .

Исходя из этого, совокупное распределение времени пребывания (F(t)) можно рассчитать как

$F(t)={\frac {C_{n}}{C_{o}}}=1-e^{-{\frac {nt}{\bar {t}}}}[1+{\frac {nt}{\bar {t}}}+{\frac {1}{2!}}({\frac {nt}{\bar {t}}})^{2}+...+{\frac {1}{(n-1)!}}({\frac {nt}{\bar {t}}})^{n-1}]$

При n → ∞ F(t) приближается к идеальному отклику PFR. Дисперсия , связанная с F(t) для импульсного стимула в каскаде CSTR, равна $\sigma _{t}^{2}={\frac {{\bar {t}}^{2}}{n}}$.

Стоимость

Первоначально стоимость снижается с увеличением количества CSTR по мере уменьшения объема, но по мере увеличения эксплуатационных расходов общие затраты в конечном итоге начинают увеличиваться.

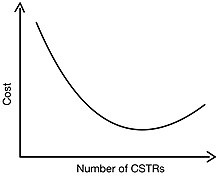
При определении стоимости серии CSTR капитальные и эксплуатационные затраты необходимо учитывать . Как видно выше, увеличение количества последовательно соединенных CSTR приведет к уменьшению общего объема реактора. Поскольку затраты масштабируются с увеличением объема, капитальные затраты снижаются за счет увеличения количества CSTR. Наибольшее снижение стоимости и, следовательно, объема происходит при использовании одного CSTR и двух последовательных CSTR. При рассмотрении эксплуатационных затрат эксплуатационные затраты зависят от количества насосов и средств управления, строительства, монтажа и обслуживания, которые сопровождают более крупные каскады. Поэтому по мере увеличения количества CSTR эксплуатационные расходы увеличиваются. Следовательно, существует минимальная стоимость, связанная с каскадом CSTR.

Реакции нулевого порядка

Из перестановки уравнения, приведенного для идентичных изотермических CSTR, протекающих в реакции нулевого порядка : $\tau ={\frac {C_{Ao}-C_{Am}}{mk}}$, объем каждого отдельного CSTR будет масштабироваться на ${\frac {1}{m}}$. Поэтому общий объем реактора не зависит от количества CSTR для реакции нулевого порядка. Следовательно, стоимость не зависит от количества реакторов для реакции нулевого порядка и не уменьшается с увеличением количества CSTR.

Селективность параллельных реакций

При рассмотрении параллельных реакций использование каскада CSTR может обеспечить большую селективность в отношении желаемого продукта.

Для данной параллельной реакции ${\ce {A -> B}}$ и ${\ce {A -> C}}$ с константами $k_{1}$ и $k_{2}$ и уравнения скорости ${\frac {d[{\ce {B}}]}{dt}}=k_{1}[{\ce {A}}]^{n_{1}}$ и ${\frac {d[{\ce {C}}]}{dt}}=k_{2}[{\ce {A}}]^{n_{2}}$соответственно, мы можем получить связь между ними, разделив ${\frac {d[{\ce {B}}]}{dt}}$ к ${\frac {d[{\ce {C}}]}{dt}}$. Поэтому ${\frac {d[{\ce {B}}]}{d[{\ce {C}}]}}={\frac {k_{1}}{k_{2}}}[{\ce {A}}]^{n_{1}-n_{2}}$. В случае, когда $n_{1}>n_{2}$ и B представляет собой желаемый продукт, каскаду CSTR благоприятствует свежий вторичный поток ${\ce {A}}$ чтобы максимизировать концентрацию ${\ce {A}}$.

Для параллельной реакции с двумя или более реагентами, такими как ${\ce {A + D -> B}}$ и ${\ce {A + D -> C}}$ с константами $k_{1}$ и $k_{2}$ и уравнения скорости ${\frac {d[{\ce {B}}]}{dt}}=k_{1}[{\ce {A}}]^{n_{1}}[{\ce {D}}]^{m_{1}}$ и ${\frac {d[{\ce {C}}]}{dt}}=k_{2}[{\ce {A}}]^{n_{2}}[{\ce {D}}]^{m_{1}2}$соответственно, мы можем получить связь между ними, разделив ${\frac {d[{\ce {B}}]}{dt}}$ к ${\frac {d[{\ce {C}}]}{dt}}$. Поэтому ${\frac {d[{\ce {B}}]}{d[{\ce {C}}]}}={\frac {k_{1}}{k_{2}}}[{\ce {A}}]^{n_{1}-n_{2}}[{\ce {D}}]^{m_{1}-m_{2}}$. В случае, когда $n_{1}>n_{2}$ и $m_{1}>m_{2}$ и B — желаемый продукт, каскад CSTR с входным потоком высокой ${\ce {[A]}}$ и ${\ce {[D]}}$ является предпочтительным. В случае, когда $n_{1}>n_{2}$ и $m_{1}<m_{2}$ и B — желаемый продукт, каскад CSTR с высокой концентрацией ${\ce {A}}$ в питающих и небольших вторичных потоках ${\ce {D}}$ является предпочтительным.

Серийные реакции, такие как ${\ce {A -> B -> C}}$ также иметь избирательность между ${\ce {B}}$ и ${\ce {C}}$ но CSTR обычно не выбираются, когда желаемый продукт ${\ce {B}}$ поскольку обратное микширование от CSTR благоприятствует ${\ce {C}}$. Обычно реактор периодического действия или PFR для этих реакций выбирают .

Приложения

CSTR облегчают быстрое разбавление реагентов путем смешивания. Следовательно, для реакций ненулевого порядка низкая концентрация реагента в реакторе означает, что CSTR будет менее эффективно удалять реагент по сравнению с PFR с тем же временем пребывания. Следовательно, CSTR обычно больше, чем PFR, что может стать проблемой в приложениях, где пространство ограничено. Однако одним из дополнительных преимуществ размывания CSTR является способность нейтрализовать потрясения в системе. В отличие от PFR, производительность CSTR менее восприимчива к изменениям состава входящей жидкости, что делает их идеальными для различных промышленных применений:

Анаэробные варочные котлы на станции очистки сточных вод Ньютаун-Крик в Гринпойнте, Бруклин

инженерия

• с использованием активного ила Процесс очистки сточных вод
• Системы очистки лагун для естественной очистки сточных вод
• Анаэробные варочные котлы для стабилизации твердых биологических веществ сточных вод
• Водно-болотные угодья для очистки сточных и ливневых вод

Химическая инженерия

• Петлевой реактор для производства фармацевтических препаратов

• Ферментация
• биогаза Производство

См. также

• Реактор ламинарного потока
• Микрореактор
• Колебательный реактор с перегородками
• Модель реактора поршневого типа