Блок сотового автомата

Блочный клеточный автомат или секционирующий клеточный автомат — это особый вид клеточного автомата, в котором решетка ячеек разбивается на непересекающиеся блоки (с разными разбиениями на разных временных шагах) и правило перехода применяется ко всему блоку за раз. а не одна клетка. Блочные клеточные автоматы полезны для моделирования физических величин, поскольку легко выбрать правила перехода, которые подчиняются физическим ограничениям, таким как законы обратимости и сохранения . ^[1]

Определение

Блочный клеточный автомат состоит из следующих компонентов: ^[1]^[2]

Регулярная решетка ячеек
Конечный набор состояний, в которых может находиться каждая клетка.
Разделение ячеек на равномерную мозаику , в которой каждая плитка раздела имеет одинаковый размер и форму.
Правило смещения раздела после каждого временного шага
Правило перехода — функция, которая принимает в качестве входных данных присвоение состояний для ячеек в одном тайле и выдает на выходе другое присвоение состояний для тех же ячеек.

На каждом временном шаге правило перехода применяется одновременно и синхронно ко всем плиткам в разделе. Затем раздел сдвигается, и та же операция повторяется на следующем временном шаге и так далее. Таким образом, как и в случае с любым клеточным автоматом, структура состояний ячеек со временем меняется для выполнения некоторых нетривиальных вычислений или моделирования.

Районы

Простейшей схемой разбиения, вероятно, является окрестность Марголуса , названная в честь Нормана Марголуса , который впервые изучал блочные клеточные автоматы с использованием этой структуры окрестностей. В окрестности Марголуса решетка разбита на $2$ -клеточные блоки (или $2\times2$ квадраты $в двух измерениях, или кубики 2\times2\times2$ в трех измерениях и т. д.), которые сдвинуты на одну ячейку (вдоль каждого измерения) на альтернативные временные шаги. ^[1]^[2]^[3]

Близкая техника, принадлежащая К. Морите и М. Харао. ^[4] состоит в разбиении каждой ячейки на конечное число частей, каждая из которых посвящена какому-то соседу. Эволюция происходит путем обмена соответствующими частями между соседями и последующего применения к каждой ячейке чисто локального преобразования. $F$ зависящий только от состояния ячейки (а не от состояний ее соседей). При такой схеме построения клеточный автомат гарантированно обратим, если локальное преобразование $F$ само по себе является биекцией . Этот метод можно рассматривать как блочный клеточный автомат на более тонкой решетке ячеек, образованной частями каждой более крупной ячейки; блоки этой более тонкой решетки чередуются между наборами частей внутри одной большой ячейки и наборами частей в соседних ячейках, которые разделяют части друг с другом.

Обратимость и сохранение

Пока правило развития каждого блока является обратимым , весь автомат также будет обратимым. Более строго в этом случае поведение автомата с обращенным во времени также можно описать как блочный клеточный автомат с той же блочной структурой и с правилом перехода, которое инвертирует исходное правило автомата внутри каждого блока. Обратное также верно: если блоки не обратимы по отдельности, глобальная эволюция не может быть обратимой: если две разные конфигурации x и y блока приводят к одному и тому же результирующему состоянию z , то глобальная конфигурация с x в одном блоке будет неотличим после одного шага от конфигурации, в которой x заменен на y . То есть клеточный автомат обратим в глобальном масштабе тогда и только тогда, когда он обратим на уровне блоков. ^[5]

Простота проектирования обратимых блочных клеточных автоматов и проверки блочных клеточных автоматов на обратимость резко контрастирует с клеточными автоматами с другими неблочными структурами окрестностей, для которых неясно, является ли автомат обратимым и для которых возможна обратная динамика. требуют гораздо более крупных окрестностей, чем прямая динамика. ^[6] Любой обратимый клеточный автомат может быть смоделирован обратимым блочным клеточным автоматом с большим числом состояний; однако из-за неразрешимости обратимости для неблочных клеточных автоматов не существует вычислимой границы радиуса областей в неблочном автомате, которые соответствуют блокам в моделировании, и перевода из неблочного правила в правило блокировки также не вычислимо. ^[7]

Блочные клеточные автоматы также представляют собой удобный формализм для разработки правил, которые, помимо обратимости, реализуют законы сохранения, такие как сохранение числа частиц, сохранение импульса и т. д. Например, если правило внутри каждого блока сохраняет число живых клеток в блоке, то глобальная эволюция автомата также сохранит то же количество. Это свойство полезно при применении клеточных автоматов к физическому моделированию. ^[8]

Моделирование обычными клеточными автоматами

Как пишут Тоффоли и Марголус: ^[2] модель блочного клеточного автомата не вносит никакой дополнительной мощности по сравнению с обычным клеточным автоматом, который использует одну и ту же структуру окрестности на каждом временном шаге: любой блочный клеточный автомат может быть смоделирован на обычном клеточном автомате, используя больше состояний и большую окрестность. В частности, пусть два автомата используют одну и ту же решетку ячеек, но пусть каждое состояние обычного автомата определяет состояние блочного автомата, фазу его шаблона смещения раздела и положение ячейки внутри его блока. Например, в случае с окрестностями Марголуса это увеличит количество состояний в восемь раз: существует четыре возможных положения, которые ячейка может занять в своем $блоке 2 \times 2$ , и две фазы разделения. При этом пусть окрестностью обычного автомата является объединение блоков, содержащих данную ячейку, в блочном клеточном автомате. Тогда с такой структурой соседства и состояния каждое обновление блочного автомата может быть смоделировано одним обновлением обычного клеточного автомата.

Приложения

Блочные клеточные автоматы обычно используются для реализации решеточных газов и других квазифизических моделей из-за простоты моделирования физических ограничений, таких как законы сохранения в этих системах. ^[1]^[8]Например, модель Марголюса можно использовать для моделирования модели решеточного газа HPP, в которой частицы движутся в двух перпендикулярных направлениях и разлетаются под прямым углом при столкновении друг с другом. В блочном клеточном моделировании этой модели правило обновления перемещает каждую ячейку в ячейку, диагонально противоположную в ее блоке, за исключением случая, когда ячейка содержит две диагонально противоположные частицы, и в этом случае они заменяются дополнительной парой диагонально противоположных частиц. частицы. Таким образом, частицы движутся по диагонали и рассеиваются в соответствии с моделью HPP. ^[2]^[9] Альтернативное правило, которое моделирует модель решетчатого газа HPP с горизонтальным и вертикальным движением частиц, а не с диагональным движением, предполагает вращение содержимого каждого блока по часовой стрелке или против часовой стрелки в чередующихся фазах, за исключением случая, когда ячейка содержит два диагонально противоположных блока. частиц, и в этом случае оно остается неизменным. ^[2]В любой из этих моделей сохраняется импульс (сумма векторов скоростей движущихся частиц), а также их количество, что является важным свойством для моделирования физических газов. Однако модели ГЭС несколько нереалистичны как модель газовой динамики, поскольку имеют дополнительные нефизические правила сохранения: сохраняется полный импульс внутри каждой линии движения, а также полный импульс всей системы. Более сложные модели, основанные на гексагональной сетке, позволяют избежать этой проблемы. ^[9]

Эти автоматы также можно использовать для моделирования движения песчинок в кучках песка и песочных часах . В этом приложении можно использовать окрестность Марголуса с правилом обновления, которое сохраняет количество зерен в каждом $блоке 2 \times 2$ , но перемещает каждое зерно как можно дальше вниз внутри своего блока. Если блок включает в себя два зерна, которые уложены вертикально друг на друга, функция перехода автомата заменяет его блоком, в котором зерна расположены рядом, что фактически позволяет высоким кучам песка опрокидываться и растекаться. Эта модель не обратима, но она все же подчиняется закону сохранения числа частиц. ^[10] Модифицированное правило, использующее ту же окрестность, но перемещающее частицы в стороны, насколько это возможно, а также вниз, позволяет моделируемым песчаным кучам распространяться, даже если они не очень крутые. ^[11] Возможны также более сложные модели песчаных кучек клеточных автоматов, включающие такие явления, как перенос ветром и трение. ^[10]

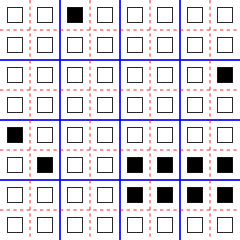
Первоначальное применение Марголусом блочной модели клеточного автомата заключалось в моделировании бильярдного шара модели обратимых вычислений , в которой логические сигналы моделируются движущимися частицами, а логические элементы моделируются упругими столкновениями этих частиц. Например, можно выполнять вычисления с бильярдным шаром в двумерной модели Марголуса с двумя состояниями на ячейку и с количеством живых ячеек, сохраняющимся в результате эволюции модели. В правиле «BBM», которое таким образом моделирует модель бильярдного шара, сигналы состоят из одиночных живых ячеек, движущихся по диагонали. Чтобы выполнить это движение, функция перехода блоков заменяет блок, содержащий одну живую ячейку, другим блоком, в котором ячейка была перемещена в противоположный угол блока. Аналогично, упругие столкновения могут выполняться с помощью функции перехода блоков, которая заменяет две диагонально противоположные живые ячейки двумя другими ячейками блока. Во всех других конфигурациях блока функция перехода блока не вносит изменений в его состояние. В этой модели $Прямоугольники 2 \times 4$ живых клеток (тщательно выровненные по отношению к перегородке) остаются стабильными и могут использоваться в качестве зеркал, чтобы направлять траектории движущихся частиц. Например, на иллюстрации окрестности Марголуса показаны четыре частицы и зеркало; если на следующем этапе используется синяя перегородка, то две частицы движутся к зеркалу, в то время как две другие собираются столкнуться, тогда как если на следующем этапе используется красная перегородка, то две частицы удаляются от зеркала, а две другие имеют только что столкнулись и будут отдаляться друг от друга. ^[3]^[5]^[12]

Дополнительные правила

Тоффоли и Марголус ^[2] предложить еще два обратимых правила для окрестности Марголуса с ячейками с двумя состояниями, которые, хотя и не мотивированы физическими соображениями, приводят к интересной динамике.

Твари

В правиле «Звери» функция перехода меняет состояние каждой ячейки в блоке, за исключением блока, состоящего ровно из двух живых ячеек, который остается неизменным. Кроме того, блоки с тремя живыми клетками подвергаются повороту на 180 градусов, а также изменению состояния. ^[2] Это обратимое правило, и оно подчиняется законам сохранения числа частиц (считая частицу живой клеткой в четных фазах и мертвой клеткой в нечетных фазах) и четности числа частиц вдоль диагональных линий. ^[12] Поскольку процесс обратим, начальные состояния, в которых все клетки принимают случайно выбранные состояния, остаются неструктурированными на протяжении всей эволюции. Однако, если начать с меньшего поля случайных клеток, сосредоточенного в большей области мертвых клеток, это правило приводит к сложной динамике, подобной той, что наблюдается в «Игре жизни» Конвея жизни, , в которой множество мелких закономерностей, похожих на планер ускользают из центральной случайной области и взаимодействовать друг с другом. ^[2]^[12] В отличие от планеров в «Жизни», обратимость и сохранение частиц вместе означают, что, когда планеры сталкиваются в «Криттерах», по крайней мере один должен спастись, и часто эти столкновения позволяют обоим приближающимся планерам восстановиться на разных исходящих траекториях. Посредством таких коллизий это правило также может моделировать вычислительную модель бильярдного шара, хотя и более сложным образом, чем правило BBM. ^[12] Правило Криттеров также может поддерживать более сложные космические корабли с разными скоростями, а также генераторы с бесконечным множеством разных периодов. ^[13]

Трон

В правиле «Трон» функция перехода оставляет каждый блок неизменным, за исключением случаев, когда все четыре его ячейки имеют одинаковое состояние, и в этом случае все их состояния меняются местами. Выполнение этого правила из начальных условий в виде прямоугольника живых клеток или аналогичных простых фигур с прямыми краями приводит к сложным прямолинейным узорам. Тоффоли и Марголус также предполагают, что это правило можно использовать для реализации правила локальной синхронизации, которое позволяет моделировать любой блочный клеточный автомат из окрестности Марголуса с использованием асинхронного клеточного автомата . В этом моделировании каждая ячейка асинхронного автомата хранит как состояние моделируемого автомата, так и второй бит, представляющий четность временной метки для этой ячейки; следовательно, полученный асинхронный автомат имеет в два раза больше состояний, чем автомат, который он моделирует. Временные метки между соседними ячейками должны отличаться не более чем на одну единицу, и любой блок из четырех ячеек, все временные метки которых имеют правильную четность, может быть обновлен в соответствии с моделируемым правилом блока. Когда выполняется обновление этого типа, четность временных меток также должна быть обновлена в соответствии с правилом Tron, которое обязательно сохраняет ограничение на соседние временные метки. Выполняя таким образом локальные обновления, эволюция каждой ячейки в асинхронном автомате идентична ее эволюции в моделируемом синхронном блочном автомате. ^[2]^[14]

См. также

Последовательность зубочисток , фрактальный узор, который можно эмулировать клеточными автоматами с окрестностями Марголуса.

Ссылки

^ Jump up to: ^а ^б ^с ^д Шифф, Джоэл Л. (2008), «4.2.1 Разделение клеточных автоматов», Клеточные автоматы: дискретный взгляд на мир , Wiley, стр. 115–116
^ Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я Тоффоли, Томмазо ; Марголус, Норман (1987), «II.12 Окрестности Марголуса», Клеточные автоматы: новая среда для моделирования , MIT Press, стр. 119–138.
^ Jump up to: ^а ^б Марголус, Н. (1984), «Физико-подобные модели вычислений», Physica D , 10 (1–2): 81–95, Бибкод : 1984PhyD...10...81M , doi : 10.1016/0167-2789 (84)90252-5 . Перепечатано в Вольфрам, Стивен , изд. (1986), Теория и приложения клеточных автоматов , Расширенная серия по сложным системам, том. 1, World Scientific, стр. 232–246.
^ Морита, К.; Харао, М. (1989), «Универсальность вычислений одномерных обратимых (инъективных) клеточных автоматов» (PDF) , Институт транзакций IEICE , E72 : 758–762
^ Jump up to: ^а ^б Дюран-Лозе, Жером (2002), «Вычисления внутри модели бильярдного шара», в Адамацки, Эндрю (ред.), Вычисления на основе столкновений , Springer-Verlag, стр. 135–160.
^ Кари, Яркко (1990), «Обратимость двумерных клеточных автоматов неразрешима», Physica D , 45 (1–3): 379–385, Bibcode : 1990PhyD...45..379K , doi : 10.1016/0167-2789( 90)90195-У
^ Кари, Яркко (1999), «О глубине схемы структурно обратимых клеточных автоматов», Fundamenta Informaticae , 38 : 93–107, doi : 10.3233/FI-1999-381208 ; Дюран-Лозе, Жером (2001), «Представление обратимых клеточных автоматов с помощью обратимых блочных клеточных автоматов» , Discrete Mathematics and Theoretical Computer Science , AA : 145–154, заархивировано из оригинала 15 мая 2011 г.
^ Jump up to: ^а ^б Вольфрам, Стивен (2002), Новый вид науки , Wolfram Media, стр. 459–464 , ISBN 1-57955-008-8
^ Jump up to: ^а ^б «5.5.4 Решеточные газы», Шифф (2008) , стр. 165–169.
^ Jump up to: ^а ^б Шопар, Бастьен; Дроз, Майкл (1998), «2.2.6 Правило кучи песка», Моделирование физических систем клеточными автоматами , Cambridge University Press, стр. 42–46.
^ Груо, Фредерик; Тромп, Джон (2000), «Клеточная гравитация» (PDF) , Parallel Processing Letters , 10 (4): 383–393, doi : 10.1142/s0129626400000354 , заархивировано из оригинала (PDF) 18 июля 2011 г.
^ Jump up to: ^а ^б ^с ^д Марголус, Норман (1999), «Кристаллические вычисления», в книге «Эй, Энтони Дж. Г. (ред.), Фейнман и вычисления» , Perseus Books, стр. 267–305, arXiv : comp-gas/9811002 , Bibcode : 1998comp.gas.11002M
^ Маротта, Себастьян М. (2005), «Жизнь в мире тварей» , Revista Ciências Exatas e Naturais , 7 (1), заархивировано из оригинала 19 марта 2012 г.
^ Оджала, Лео; Пенттинен, Олли-Матти; Парвиайнен, Элина (2004), «Моделирование и анализ квантово-клеточных автоматов Марголуса с использованием методов теории сетей», Приложения и теория сетей Петри 2004 , Конспекты лекций по информатике, том. 3099, Springer-Verlag, стр. 331–350, номер документа : 10.1007/978-3-540-27793-4_19.

Внешние ссылки

Моделирование тварей , Сет Келер, Univ. Флориды

[schiff-1] Jump up to: ^а ^б ^с ^д Шифф, Джоэл Л. (2008), «4.2.1 Разделение клеточных автоматов», Клеточные автоматы: дискретный взгляд на мир , Wiley, стр. 115–116

[tm-2] Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я Тоффоли, Томмазо ; Марголус, Норман (1987), «II.12 Окрестности Марголуса», Клеточные автоматы: новая среда для моделирования , MIT Press, стр. 119–138.

[m84-3] Jump up to: ^а ^б Марголус, Н. (1984), «Физико-подобные модели вычислений», Physica D , 10 (1–2): 81–95, Бибкод : 1984PhyD...10...81M , doi : 10.1016/0167-2789 (84)90252-5 . Перепечатано в Вольфрам, Стивен , изд. (1986), Теория и приложения клеточных автоматов , Расширенная серия по сложным системам, том. 1, World Scientific, стр. 232–246.

[4] Морита, К.; Харао, М. (1989), «Универсальность вычислений одномерных обратимых (инъективных) клеточных автоматов» (PDF) , Институт транзакций IEICE , E72 : 758–762

[bbm-5] Jump up to: ^а ^б Дюран-Лозе, Жером (2002), «Вычисления внутри модели бильярдного шара», в Адамацки, Эндрю (ред.), Вычисления на основе столкновений , Springer-Verlag, стр. 135–160.

[6] Кари, Яркко (1990), «Обратимость двумерных клеточных автоматов неразрешима», Physica D , 45 (1–3): 379–385, Bibcode : 1990PhyD...45..379K , doi : 10.1016/0167-2789( 90)90195-У

[7] Кари, Яркко (1999), «О глубине схемы структурно обратимых клеточных автоматов», Fundamenta Informaticae , 38 : 93–107, doi : 10.3233/FI-1999-381208 ; Дюран-Лозе, Жером (2001), «Представление обратимых клеточных автоматов с помощью обратимых блочных клеточных автоматов» , Discrete Mathematics and Theoretical Computer Science , AA : 145–154, заархивировано из оригинала 15 мая 2011 г.

[nkos-8] Jump up to: ^а ^б Вольфрам, Стивен (2002), Новый вид науки , Wolfram Media, стр. 459–464 , ISBN 1-57955-008-8

[schiff2-9] Jump up to: ^а ^б «5.5.4 Решеточные газы», Шифф (2008) , стр. 165–169.

[sandpile-10] Jump up to: ^а ^б Шопар, Бастьен; Дроз, Майкл (1998), «2.2.6 Правило кучи песка», Моделирование физических систем клеточными автоматами , Cambridge University Press, стр. 42–46.

[11] Груо, Фредерик; Тромп, Джон (2000), «Клеточная гравитация» (PDF) , Parallel Processing Letters , 10 (4): 383–393, doi : 10.1142/s0129626400000354 , заархивировано из оригинала (PDF) 18 июля 2011 г.

[cc-12] Jump up to: ^а ^б ^с ^д Марголус, Норман (1999), «Кристаллические вычисления», в книге «Эй, Энтони Дж. Г. (ред.), Фейнман и вычисления» , Perseus Books, стр. 267–305, arXiv : comp-gas/9811002 , Bibcode : 1998comp.gas.11002M

[marotta-13] Маротта, Себастьян М. (2005), «Жизнь в мире тварей» , Revista Ciências Exatas e Naturais , 7 (1), заархивировано из оригинала 19 марта 2012 г.

[14] Оджала, Лео; Пенттинен, Олли-Матти; Парвиайнен, Элина (2004), «Моделирование и анализ квантово-клеточных автоматов Марголуса с использованием методов теории сетей», Приложения и теория сетей Петри 2004 , Конспекты лекций по информатике, том. 3099, Springer-Verlag, стр. 331–350, номер документа : 10.1007/978-3-540-27793-4_19.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]