Нельсон рулит
Правила Нельсона — это метод управления процессом , позволяющий определить, вышла ли некоторая измеряемая переменная из-под контроля (непредсказуемая или последовательная). Правила обнаружения «выходящих из-под контроля» или неслучайных состояний были впервые постулированы Уолтером А. Шухартом. [1] в 1920-е годы. Правила Нельсона были впервые опубликованы в октябрьском выпуске журнала Quality Technology за 1984 год в статье Ллойда С. Нельсона . [2]
Правила применяются к контрольной диаграмме зависимость величины некоторой переменной , на которой отображается от времени. Правила основаны на среднем значении и стандартном отклонении выборок.
| Правило | Описание | Пример диаграммы | Указана проблема |
|---|---|---|---|
Правило 1 | Один балл составляет более 3 стандартных отклонений от среднего значения. |  | Один образец (в данном случае показаны два) полностью вышел из-под контроля. |
Правило 2 | Девять (или более) точек подряд находятся по одну сторону от среднего. | 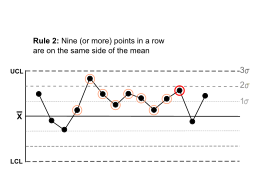 | Существует некоторая продолжительная предвзятость . |
Правило 3 | Шесть (или более) пунктов подряд непрерывно увеличиваются (или уменьшаются). | Тенденция . существует | |
Правило 4 | Четырнадцать (или более) точек подряд чередуются по направлению, то увеличиваясь, то уменьшаясь. | 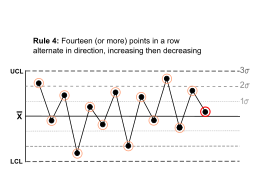 | Такое сильное колебание находится за пределами шума . Обратите внимание, что правило касается только направленности. Положение среднего значения и размер стандартного отклонения не имеют значения. |
Правило 5 | Две (или три) из трех точек подряд имеют более 2 стандартных отклонений от среднего значения в одном и том же направлении. |  | Существует средняя тенденция к выходу выборок из-под контроля. Сторона среднего значения для третьей точки не указана. |
Правило 6 | Четыре (или пять) из пяти точек подряд имеют более 1 стандартного отклонения от среднего значения в одном и том же направлении. | 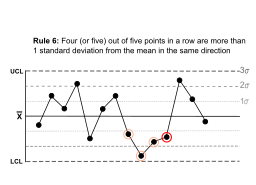 | Существует сильная тенденция к тому, что выборки выходят из-под контроля. Сторона среднего значения пятой точки не указана. |
Правило 7 | Все пятнадцать точек подряд находятся в пределах 1 стандартного отклонения от среднего значения по обе стороны от среднего значения. |  | При 1 стандартном отклонении можно было бы ожидать большего разнообразия. |
Правило 8 | Существует восемь точек подряд, но ни одна из них не находится в пределах 1 стандартного отклонения от среднего значения, а точки расположены в обоих направлениях от среднего значения. | 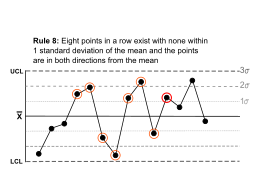 | Прыжок сверху вниз при пропуске первой полосы стандартного отклонения редко бывает случайным. |
Вышеупомянутые восемь правил применяются к диаграмме с переменным значением.
Вторую диаграмму, диаграмму скользящего диапазона , также можно использовать, но только с правилами 1, 2, 3 и 4. Такая диаграмма строит график максимального значения - минимального значения N соседних точек в зависимости от временной выборки диапазона.
Пример диапазона перемещения: если N = 3 и значения равны 1, 3, 5, 3, 3, 2, 4, 5, то наборы соседних точек равны (1,3,5) (3,5,3) (5 ,3,3) (3,3,2) (3,2,4) (2,4,5), что приводит к значениям диапазона перемещения (5-1) (5-3) (5-3) (3- 2) (4-2) (5-2) = 4, 2, 2, 1, 2, 3.
Применение этих правил указывает на возникновение потенциальной «вышедшей из-под контроля» ситуации. Однако всегда будут ложные оповещения, и чем больше правил будет применено, тем больше их будет. Для некоторых процессов может быть полезно опустить одно или несколько правил. Точно так же могут отсутствовать некоторые оповещения, когда не обнаружена какая-то конкретная «вышедшая из-под контроля» ситуация. Эмпирически точность обнаружения хорошая.
См. также
[ редактировать ]- Общая причина и особая причина
- Статистический контроль процессов
- Правила Вестерн Электрик
- Правила Вестгарда
- Американское общество качества , инструменты качества
Ссылки
[ редактировать ]- ^ Справочник по инженерной статистике 6.3.2 , Электронный справочник NIST/SEMATECH по статистическим методам, Национальный институт стандартов и технологий , декабрь 2006 г.
- ^ Ллойд С. Нельсон, «Контрольная карта Шухарта - тесты для особых случаев». Журнал технологий качества 16, вып. 4 (октябрь 1984 г.), 238–239. https://doi.org/10.1080/00224065.1984.11978921