Линейный классификатор

В области машинного обучения цель статистической классификации — использовать характеристики объекта для определения того, к какому классу (или группе) он принадлежит. Линейный классификатор достигает этого, принимая решение о классификации на основе значения линейной комбинации характеристик. Характеристики объекта также известны как значения признаков и обычно представляются машине в виде вектора, называемого вектором признаков . Такие классификаторы хорошо работают для практических задач, таких как классификация документов , и в более общем плане для задач со многими переменными ( особенностями ), достигая уровня точности, сравнимого с нелинейными классификаторами, и при этом требуя меньше времени для обучения и использования. ^[1] 5–12–23

Определение [ править ]

Если входной вектор признаков классификатора является действительным вектором ${\vec {x}}$ , то выходной балл равен

y=f({\vec {w}}\cdot {\vec {x}})=f\left(\sum _{j}w_{j}x_{j}\right),

где ${\vec {w}}$ — действительный вектор весов, а f — функция, которая преобразует скалярное произведение двух векторов в желаемый результат. (Другими словами, ${\vec {w}}$ является одноформовым или линейным функциональным отображением ${\vec {x}}$ на R .) Весовой вектор ${\vec {w}}$ изучается из набора помеченных обучающих образцов. Часто f является пороговой функцией , которая отображает все значения ${\vec {w}}\cdot {\vec {x}}$ выше определенного порога для первого класса и всех других значений для второго класса; например,

f(\mathbf {x} )={\begin{cases}1&{\text{if }}\ \mathbf {w} ^{T}\cdot \mathbf {x} >\theta ,\\0&{\text{otherwise}}\end{cases}}

Верхний индекс T указывает на транспонирование и $\theta$ является скалярным порогом. Более сложное f может дать вероятность того, что элемент принадлежит определенному классу.

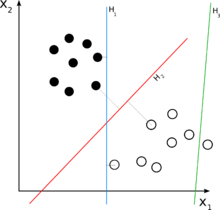
Для задачи классификации двух классов можно визуализировать работу линейного классификатора как разделение многомерного входного пространства гиперплоскостью : все точки на одной стороне гиперплоскости классифицируются как «да», а другие классифицируются как "нет".

Линейный классификатор часто используется в ситуациях, когда скорость классификации является проблемой, поскольку зачастую он является самым быстрым классификатором, особенно когда ${\vec {x}}$ является редким. Кроме того, линейные классификаторы часто работают очень хорошо, когда количество измерений в ${\vec {x}}$ является большим, как в классификации документов , где каждый элемент в ${\vec {x}}$ обычно это количество вхождений слова в документ (см. матрицу терминов документа ). В таких случаях классификатор должен быть хорошо регуляризован .

Генеративные модели дискриминативных против моделей

Существует два широких класса методов определения параметров линейного классификатора. ${\vec {w}}$ . Это могут быть генеративные и дискриминативные модели. ^[2]^[3] Методы первой модели совместного распределения вероятностей , тогда как методы второй модели являются функциями условной плотности. $P({\rm {class}}|{\vec {x}})$ . Примеры таких алгоритмов включают в себя:

Линейный дискриминантный анализ (LDA) — предполагает использование гауссовских моделей условной плотности.
Наивный байесовский классификатор с многочленными или многомерными моделями событий Бернулли.

Второй набор методов включает в себя дискриминационные модели , которые пытаются максимизировать качество результатов обучающего набора . Дополнительные члены в функции стоимости обучения могут легко выполнить регуляризацию окончательной модели. Примеры дискриминационного обучения линейных классификаторов включают:

Логистическая регрессия — оценка максимального правдоподобия ${\vec {w}}$ предполагая, что наблюдаемый обучающий набор был создан с помощью биномиальной модели, которая зависит от выходных данных классификатора.
Персептрон — алгоритм, который пытается исправить все ошибки, встречающиеся в обучающем наборе.
Линейный дискриминантный анализ Фишера — алгоритм (отличный от «LDA»), который максимизирует соотношение разброса между классами и разброса внутри класса без каких-либо других предположений. По сути, это метод уменьшения размерности для двоичной классификации. ^[4]
Машина опорных векторов — алгоритм, который максимизирует разницу между гиперплоскостью решения и примерами в обучающем наборе.

Примечание. Несмотря на свое название, LDA не принадлежит к классу дискриминативных моделей в этой таксономии. Однако его название имеет смысл, когда мы сравниваем LDA с другим основным алгоритмом уменьшения линейной размерности : анализом главных компонентов (PCA). LDA — это алгоритм обучения с учителем , который использует метки данных, а PCA — это алгоритм обучения без учителя , который игнорирует метки. Подводя итог, можно сказать, что название является историческим артефактом. ^[5]^: 117

Дискриминационное обучение часто дает более высокую точность, чем моделирование функций условной плотности. ^{[ нужна ссылка ]}. Однако обрабатывать недостающие данные часто проще с помощью моделей условной плотности. ^{[ нужна ссылка ]}.

Все перечисленные выше алгоритмы линейного классификатора можно преобразовать в нелинейные алгоритмы, работающие в другом входном пространстве. $\varphi ({\vec {x}})$ , используя трюк ядра .

обучение Дискриминационное

Дискриминационное обучение линейных классификаторов обычно происходит контролируемым образом с помощью алгоритма оптимизации , которому предоставляется обучающий набор с желаемыми выходными данными и функция потерь , которая измеряет несоответствие между выходными данными классификатора и желаемыми выходными данными. Таким образом, алгоритм обучения решает оптимизационную задачу вида ^[1]

{\underset {\mathbf {w} }{\arg \min }}\;R(\mathbf {w} )+C\sum _{i=1}^{N}L(y_{i},\mathbf {w} ^{\mathsf {T}}\mathbf {x} _{i})

где

$w$ — вектор параметров классификатора,
$Л (йи, ш Т x i)$ — это функция потерь, которая измеряет несоответствие между прогнозом классификатора и истинным выходным сигналом $y i$ для $i$ -го обучающего примера,
$R (w)$ — функция регуляризации , которая предотвращает слишком большие размеры параметров (вызывая переобучение ), и
$C$ — скалярная константа (задаваемая пользователем алгоритма обучения), которая контролирует баланс между регуляризацией и функцией потерь.

Популярные функции потерь включают шарнирные потери (для линейных SVM) и логарифмические потери (для линейной логистической регрессии). Если функция регуляризации $R$ выпукла , то описанная выше задача является выпуклой . ^[1] Существует множество алгоритмов для решения таких задач; Популярные методы линейной классификации включают ( стохастический ) градиентный спуск , L-BFGS , координатный спуск и методы Ньютона .

См. также [ править ]

Примечания [ править ]

↑ Перейти обратно: Перейти обратно: ^а ^б ^с Го-Сюнь Юань; Чиа-Хуа Хо; Чи-Джень Линь (2012). «Последние достижения крупномасштабной линейной классификации» (PDF) . Учеб. ИИЭЭ . 100 (9). Архивировано (PDF) из оригинала 10 июня 2017 г.
^ Т. Митчелл, Генеративные и дискриминационные классификаторы: наивный Байес и логистическая регрессия. Черновая версия, 2005 г.
^ AY Ng и MI Jordan. О дискриминативных и генеративных классификаторах: сравнение логистической регрессии и наивного Байеса. в НИПС 14, 2002 г.
^ Р.О. Дуда, П.Е. Харт, Д.Г. Сторк, «Классификация шаблонов», Wiley, (2001). ISBN 0-471-05669-3
^ Р.О. Дуда, П.Е. Харт, Д.Г. Сторк, «Классификация шаблонов», Wiley, (2001). ISBN 0-471-05669-3

Дальнейшее чтение [ править ]

Ю. Ян, С. Лю, «Пересмотр категоризации текста», Proc. Конференция ACM SIGIR, стр. 42–49 (1999). бумага @ citeseer
Р. Хербрич, «Изучение классификаторов ядра: теория и алгоритмы», MIT Press, (2001). ISBN 0-262-08306-X

[ieee-1] Перейти обратно: Перейти обратно: ^а ^б ^с Го-Сюнь Юань; Чиа-Хуа Хо; Чи-Джень Линь (2012). «Последние достижения крупномасштабной линейной классификации» (PDF) . Учеб. ИИЭЭ . 100 (9). Архивировано (PDF) из оригинала 10 июня 2017 г.

[2] Т. Митчелл, Генеративные и дискриминационные классификаторы: наивный Байес и логистическая регрессия. Черновая версия, 2005 г.

[3] AY Ng и MI Jordan. О дискриминативных и генеративных классификаторах: сравнение логистической регрессии и наивного Байеса. в НИПС 14, 2002 г.

[4] Р.О. Дуда, П.Е. Харт, Д.Г. Сторк, «Классификация шаблонов», Wiley, (2001). ISBN 0-471-05669-3

[5] Р.О. Дуда, П.Е. Харт, Д.Г. Сторк, «Классификация шаблонов», Wiley, (2001). ISBN 0-471-05669-3

[1]

[2]

[3]

[4]

[5]