Уравнение Тейта

В механике жидкости уравнение Тейта представляет собой уравнение состояния , используемое для связи плотности жидкости с гидростатическим давлением . Уравнение было первоначально опубликовано Питером Гатри Тейтом в 1888 году в форме

${\frac {V_{0}-V}{PV_{0}}}={\frac {A}{\Pi +P}}$

где $P$ – гидростатическое давление помимо атмосферного, $V_{0}$ - объем при атмосферном давлении, $V$ объем под дополнительным давлением $P$, и $A,\Pi$ – экспериментально определяемые параметры. Очень подробное историческое исследование уравнения Тейта с физической интерпретацией двух параметров. $A$ и $\Pi$ дано в ссылке.

Уравнение состояния Тейта-Таммана

В 1895 году исходное изотермическое уравнение Тейта было заменено Тамманом на уравнение вида

${K}=-{V_{0}}\left({\frac {\partial P}{\partial V}}\right)_{T}={V_{0}}{\frac {(B+P)}{C}}$

где $K$ – изотермический смешанный модуль объемного сжатия. Это приведенное выше уравнение широко известно как уравнение Тейта . Интегрированная форма обычно пишется

$V=V_{0}-C\log \left({\frac {B+P}{B+P_{0}}}\right)$

где

• $V\$ – удельный объем вещества (в единицах мл / г или м ³ /кг)
• $V_{0}$ это удельный объем при $P=P_{0}$
• $B\$ (те же единицы, что и $P_{0}$) и $C\$ (те же единицы, что и $V_{0}$) являются функциями температуры

Формула давления

Выражение давления через удельный объем имеет вид

$P=(B+P_{0})\exp \left(-{\frac {V-V_{0}}{C}}\right)-B\,.$

Очень подробное исследование уравнения состояния Тейта-Таммана с физической интерпретацией двух эмпирических параметров. $C$ и $B$ приведен в главе 3 справочника. Выражения в зависимости от температуры для двух эмпирических параметров $C$ и $B$ даны для воды, морской воды, гелия-4 и гелия-3 во всей жидкой фазе до критической температуры. $T_{c}$. Особый случай переохлажденной фазы воды обсуждается в справочном приложении D. Случай жидкого аргона между температурой тройной точки и 148 К подробно рассмотрен в разделе 6 справочника.

Уравнение состояния Тейта-Мурнагана

Удельный объем как функция давления, предсказанная уравнением состояния Тейта-Мурнагана.

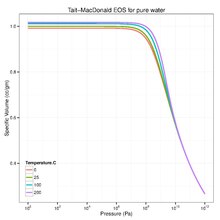
Еще одно популярное изотермическое уравнение состояния, известное под названием «уравнение Тейта». это модель Мурнагана что иногда выражается как

${\frac {V}{V_{0}}}=\left[1+{\frac {n}{K_{0}}}\,(P-P_{0})\right]^{-1/n}$

где $V$ удельный объем под давлением $P$, $V_{0}$ удельный объем под давлением $P_{0}$, $K_{0}$ объемный модуль при $P_{0}$, и $n$ является материальным параметром.

Формула давления

Это уравнение в форме давления можно записать как

$P={\frac {K_{0}}{n}}\left[\left({\frac {V_{0}}{V}}\right)^{n}-1\right]+P_{0}={\frac {K_{0}}{n}}\left[\left({\frac {\rho }{\rho _{0}}}\right)^{n}-1\right]+P_{0}.$

где $\rho ,\rho _{0}$ плотности массы при $P,P_{0}$, соответственно. Для чистой воды типичные параметры: $P_{0}$ = 101,325 Па, $\rho _{0}$ = 1000 кг/куб.м, $K_{0}$ = 2,15 ГПа, и $n$ = 7.15.

Обратите внимание, что эта форма уравнения состояния Тейта идентична форме уравнения состояния Мурнагана .

Формула объемного модуля

Касательный модуль объемного сжатия, предсказанный моделью Макдональда – Тейта, равен

$K=K_{0}\left({\frac {V_{0}}{V}}\right)^{n}\,.$

Уравнение состояния Тумлирца – Таммана – Тейта

Уравнение состояния Тумлирца-Таммана-Тейта, основанное на экспериментальных данных по чистой воде.

Родственное уравнение состояния, которое можно использовать для моделирования жидкостей, - это уравнение Тумлирца (иногда называемое уравнением Таммана и первоначально предложенное Тумлирцем в 1909 году и Тамманном в 1911 году для чистой воды). Это отношение имеет вид

$V(P,S,T)=V_{\infty }-K_{1}S+{\frac {\lambda }{P_{0}+K_{2}S+P}}$

где $V(P,S,T)$ это удельный объем, $P$ это давление, $S$ это соленость, $T$ это температура, и $V_{\infty }$ - удельный объем, когда $P=\infty$, и $K_{1},K_{2},P_{0}$ параметры, которые можно подогнать под экспериментальные данные.

Версия Тумлирца–Таммана уравнения Тейта для пресной воды, т.е. когда $S=0$, является

$V=V_{\infty }+{\frac {\lambda }{P_{0}+P}}\,.$

Для чистой воды температурная зависимость $V_{\infty },\lambda ,P_{0}$ являются:

${\begin{aligned}\lambda &=1788.316+21.55053\,T-0.4695911\,T^{2}+3.096363\times 10^{-3}\,T^{3}-0.7341182\times 10^{-5}\,T^{4}\\P_{0}&=5918.499+58.05267\,T-1.1253317\,T^{2}+6.6123869\times 10^{-3}\,T^{3}-1.4661625\times 10^{-5}\,T^{4}\\V_{\infty }&=0.6980547-0.7435626\times 10^{-3}\,T+0.3704258\times 10^{-4}\,T^{2}-0.6315724\times 10^{-6}\,T^{3}\\&+0.9829576\times 10^{-8}\,T^{4}-0.1197269\times 10^{-9}\,T^{5}+0.1005461\times 10^{-11}\,T^{6}\\&-0.5437898\times 10^{-14}\,T^{7}+0.169946\times 10^{-16}\,T^{8}-0.2295063\times 10^{-19}\,T^{9}\end{aligned}}$

В приведенных выше условиях температура $T$ в градусах Цельсия, $P_{0}$ находится в барах, $V_{\infty }$ находится в куб.см/г, и $\lambda$ находится в барах-см3/г.

Формула давления

Обратная зависимость Тумлирца – Таммана – Тейта для давления как функции удельного объема имеет вид

$P={\frac {\lambda }{V-V_{\infty }}}-P_{0}\,.$

Формула объемного модуля

Формула Тумлирца-Таммана-Тейта для мгновенного касательного модуля объемного сжатия чистой воды представляет собой квадратичную функцию $P$ (альтернативный вариант см. )

$K=-V\,{\frac {\partial P}{\partial V}}={\frac {V\,\lambda }{(V-V_{\infty })^{2}}}=(P_{0}+P)+{\frac {V_{\infty }}{\lambda }}(P_{0}+P)^{2}\,.$

Модифицированное уравнение состояния Тейта

В частности, после изучения подводных взрывов и, точнее, излучаемых ударных волн, Дж. Г. Кирквуд в 1965 г. предложил более подходящая форма уравнения состояния для описания высоких давлений (> 1 кбар) путем выражения коэффициента изэнтропической сжимаемости как

$-{\frac {1}{V}}\left({\frac {\partial V}{\partial P}}\right)_{S}={\frac {1}{n(B+P)}}$

где $S$ представляет здесь энтропию. Два эмпирических параметра $n$ и $B$ теперь являются функцией энтропии, такой что

• $n\$ безразмерен
• $B\$ имеет те же единицы измерения, что и $P$

Интегрирование приводит к следующему выражению для объема $V(P,S)$ вдоль изэнтропы $S$

${\frac {V}{V_{0}}}=\left(1+{\frac {P_{0}}{B}}\right)^{1/n}\left(1+{\frac {P}{B}}\right)^{-1/n}$

где $V_{0}=V(P_{0},S)$.

Формула давления

Выражение для давления $P(V,S)$ в терминах удельного объема по изэнтропе $S$ является

$P=(B+P_{0})\,\left({\cfrac {V_{0}}{V}}\right)^{n}-B\,.$

Очень подробное исследование модифицированного уравнения состояния Тейта с физической интерпретацией двух эмпирических параметров. $n$ и $B$ приведен в главе 4 справочника. Выражения как функция энтропии для двух эмпирических параметров $n$ и $B$ даны для воды, гелия-3 и гелия-4.

См. также

• Уравнение состояния