Ненейтральная плазма

В физике ненейтральная плазма — это плазма , суммарный заряд которой создает достаточно большое электрическое поле, чтобы играть важную или даже доминирующую роль в динамике плазмы. Простейшая ненейтральная плазма — это плазма, состоящая из одного вида заряда. Примерами ненейтральной плазмы одного вида, созданной в лабораторных экспериментах, являются плазма, полностью состоящая из электронов . чистая ионная плазма , позитронная плазма , и антипротонная плазма.

Ненейтральная плазма используется для исследования основных плазменных явлений, таких как перенос перекрестного магнитного поля, нелинейные вихревые взаимодействия, плазменные волны и нестабильности . Их также использовали для создания холодной нейтральной антиматерии путем тщательного смешивания и рекомбинации криогенной чистой позитронной и чистой антипротонной плазмы. Позитронная плазма также используется в экспериментах по атомной физике , изучающих взаимодействие антивещества с нейтральными атомами и молекулами. Криогенная чистая ионная плазма использовалась в исследованиях сильносвязанной плазмы. и квантовая запутанность . Более прозаично, что чистая электронная плазма используется для производства микроволн в микроволновых печах за счет магнетронной нестабильности .

Нейтральная плазма, контактирующая с твердой поверхностью (то есть большинство лабораторной плазмы), обычно ненейтральна в своих краевых областях. Из-за неравной скорости потерь электронов и ионов на поверхности создается электрическое поле ( «амбиполярное поле» ), которое сдерживает более мобильные виды до тех пор, пока скорости потерь не станут одинаковыми. Электростатический потенциал (измеренный в электрон-вольтах), необходимый для создания этого электрического поля, зависит от многих переменных, но часто бывает порядка температуры электронов.

Ненейтральная плазма, у которой все виды имеют одинаковый знак заряда, обладает исключительными удерживающими свойствами по сравнению с нейтральной плазмой. Их можно удержать в состоянии теплового равновесия , используя только статические электрические и магнитные поля, в конфигурации ловушки Пеннинга (см. рис. 1). Время задержания достигло нескольких часов. Используя метод «вращающейся стены» , время удержания плазмы может быть увеличено произвольно.

Такая ненейтральная плазма также может получить доступ к новым состояниям материи. Например, их можно охладить до криогенных температур без рекомбинации (поскольку нет противоположно заряженных частиц, с которыми можно было бы рекомбинировать). Если температура достаточно низкая (обычно порядка 10 мК), плазма может стать ненейтральной жидкостью или кристаллом . Объемно -центрированная кубическая структура этих плазменных кристаллов наблюдалась методом брэгговского рассеяния в экспериментах с лазерно-охлажденной плазмой чистого бериллия.

Равновесие одновидовой ненейтральной плазмы

Рис. 1. Схема ненейтральной плазмы, удерживаемой в ловушке Пеннинга .

Ненейтральную плазму с одним знаком заряда можно удерживать в течение длительного периода времени, используя только статические электрические и магнитные поля. Одна из таких конфигураций называется ловушкой Пеннинга , в честь изобретателя Ф.М. Пеннинга . Цилиндрическую версию ловушки также иногда называют ловушкой Пеннинга-Мальмберга в честь профессора Джона Мальмберга. Ловушка состоит из нескольких цилиндрически-симметричных электродов и однородного магнитного поля, приложенного вдоль оси ловушки (рис. 1). Плазма удерживается в осевом направлении путем смещения концевых электродов так, чтобы создать аксиальную потенциальную яму, которая будет улавливать заряды заданного знака (на рисунке знак считается положительным). В радиальном направлении удержание обеспечивается силой v × B Лоренца , обусловленной вращением плазмы вокруг оси ловушки. Вращение плазмы вызывает направленную внутрь силу Лоренца, которая просто уравновешивает направленные наружу силы, вызванные ненейтрализованной плазмой, а также центробежную силу. Математически баланс радиальных сил подразумевает баланс между электрическими, магнитными и центробежными силами:

$0=qE_{r}+qv_{\theta }B+m{v_{\theta }}^{2}/r,$ ( 1 )

где m — масса частицы, q — заряд частицы, r — радиальное расстояние от оси ловушки, а E _r — радиальная составляющая электрического поля. Это квадратное уравнение можно решить относительно скорости вращения $v_{\theta }$, что приводит к двум решениям: медленному вращению и быстрому вращению. Скорость вращения $\omega =-v_{\theta }/r$ для этих двух решений можно записать как

$\omega ={\frac {\Omega _{c}}{2}}\pm {\sqrt {{\Omega _{c}}^{2}/4-qE_{r}/{mr}}}$,

где $\Omega _{c}=qB/m$ – циклотронная частота . В зависимости от радиального электрического поля решения для скорости вращения попадают в диапазон $0\leq \omega /\Omega _{c}\leq 1$. Режимы медленного и быстрого вращения встречаются, когда электрическое поле таково, что $qE_{r}/{mr}={\Omega _{c}}^{2}/4$. Это называется пределом Бриллюэна; это уравнение максимально возможного радиального электрического поля, обеспечивающего удержание плазмы.

Рис. 2. Зависимость плотности от скорости вращения однокомпонентной плазмы, удерживаемой в ловушке Пеннинга .

Это радиальное электрическое поле можно связать с плотностью плазмы n через уравнение Пуассона :

${\frac {1}{r}}{\frac {\partial }{\partial r}}(rE_{r})=qn/\epsilon _{0},$

и это уравнение можно использовать для получения связи между плотностью и скоростью вращения плазмы. Если предположить, что скорость вращения одинакова по радиусу (т.е. плазма вращается как твердое тело), ​​то уравнение Из (1) следует, что радиальное электрическое поле пропорционально радиусу r . Решая E _r из этого уравнения в терминах $\omega$ и подстановка результата в уравнение Пуассона дает

$n={\frac {2\epsilon _{0}m\omega (\Omega _{c}-\omega )}{q^{2}}}.$ ( 2 )

Из этого уравнения следует, что максимально возможная плотность возникает в пределе Бриллюэна и имеет значение

$n_{B}={\frac {\epsilon _{0}m{\Omega _{c}}^{2}}{2q^{2}}}={\frac {B^{2}/(2\mu _{0})}{mc^{2}}}$

где $c=1/{\sqrt {\mu _{0}\epsilon _{0}}}$ это скорость света. Таким образом, плотность энергии покоя плазмы, n·m·c ² , меньше или равна плотности магнитной энергии $B^{2}/(2\mu _{0})$ магнитного поля. Это достаточно жесткое требование к плотности. Для магнитного поля силой 10 Тл плотность Бриллюэна для электронов составляет всего n _B = 4,8 × 10 ¹⁴ см ⁻³ .

Плотность, предсказанная уравнением (2), масштабированная по плотности Бриллюэна, показана как функция скорости вращения на рис. (2). Две скорости вращения дают одинаковую плотность, что соответствует решениям с медленным и быстрым вращением.

Процессы потери плазмы; метод вращающейся стены

Основная статья: Техника вращающейся стены

В экспериментах с однокомпонентной плазмой скорости вращения плазмы в диапазоне десятков кГц нередки, даже в режиме медленного вращения. Это быстрое вращение необходимо, чтобы обеспечить удерживающую плазму радиальную силу Лоренца. Однако, если в ловушке есть нейтральный газ, столкновения между плазмой и газом приводят к замедлению вращения плазмы, что приводит к радиальному расширению плазмы до тех пор, пока она не войдет в контакт с окружающими электродами и не потеряется. Этот процесс потерь можно смягчить, если использовать ловушку в сверхвысоком вакууме. Однако даже в таких условиях вращение плазмы все же может быть замедлено за счет взаимодействия плазмы с «ошибками» во внешних удерживающих полях. Если эти поля не являются идеально цилиндрически симметричными, асимметрия может воздействовать на плазму, снижая скорость вращения. Такие полевые ошибки неизбежны в любом реальном эксперименте и ограничивают время удержания плазмы.

Этот механизм потери плазмы можно преодолеть, применив к плазме ошибку вращающегося поля. Если ошибка вращается быстрее, чем плазма, она раскручивает плазму (аналогично тому, как вращающаяся лопасть блендера заставляет вращаться пищу), противодействуя эффекту ошибок поля, которые являются стационарными в рамках лаборатории. Эту ошибку вращающегося поля называют «вращающейся стеной» в честь теоретической идеи о том, что можно обратить вспять эффект асимметрии ловушки, просто вращая всю ловушку с частотой вращения плазмы. Поскольку это непрактично, вместо этого вращают электрическое поле ловушки, а не всю ловушку, подавая подходящие фазированные напряжения на набор электродов, окружающих плазму.

Криогенная ненейтральная плазма: коррелированные состояния

Рис. 3. Ложноцветное изображение УФ - лазера , подвергшегося брэгговскому рассеянию на чистом ионном кристалле .

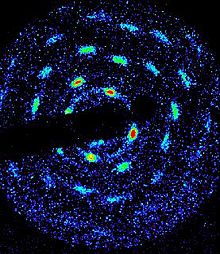
Когда ненейтральная плазма охлаждается до криогенных температур, она не рекомбинирует в нейтральный газ, как нейтральная плазма, потому что нет противоположно заряженных частиц, с которыми можно было бы рекомбинировать. В результате система может получить доступ к новым сильно связанным ненейтральным состояниям материи, включая плазменные кристаллы, состоящие исключительно из одного вида заряда. Эта сильносвязанная ненейтральная плазма параметризуется параметром связи Γ, определяемым как

$\Gamma ={\frac {q^{2}}{4\pi \epsilon _{0}k_{B}Ta}},$

где $T$ это температура и $a$ - это радиус Вигнера – Зейтца (или среднее расстояние между частицами), выраженный через плотность $n$ по выражению $4\pi a^{3}n/3=1$. Параметр связи можно рассматривать как отношение средней энергии взаимодействия между парами ближайших соседей: $q^{2}/(4\pi \epsilon _{0}a)$, а средняя кинетическая энергия порядка $k_{b}T$. Когда это отношение мало, взаимодействия слабы и плазма представляет собой почти идеальный газ зарядов, движущихся в среднем поле, создаваемом другими зарядами. Однако, когда $\Gamma >1$ Взаимодействия между частицами важны, и плазма ведет себя скорее как жидкость или даже кристалл, если $\Gamma$ достаточно велик. Фактически, компьютерное моделирование и теория предсказали, что в бесконечной однородной плазме система демонстрирует постепенное появление ближнего порядка, соответствующего жидкоподобному состоянию для $\Gamma \approx 2$, и прогнозируется фазовый переход первого рода к объемно-центрированному кубическому кристаллу для $\Gamma \simeq 175$.

Эксперименты наблюдали это кристаллическое состояние в плазме чистых ионов бериллия, охлажденной лазером до температур милликельвинового диапазона. Среднее расстояние между частицами в этом чистом ионном кристалле было порядка 10-20 мкм , что намного больше, чем в нейтральном кристаллическом веществе. Это расстояние соответствует плотности порядка 10 ⁸ -10 ⁹ см ⁻³ , что несколько меньше предела Бриллюэна для бериллия в магнитном поле эксперимента 4,5 Тл. Криогенные температуры тогда были необходимы для того, чтобы получить $\Gamma$ значение в режиме сильной связи. В экспериментах измерялась кристаллическая структура методом брэгговского рассеяния , при котором коллимированный лазерный луч рассеивался на кристалле, демонстрируя брэгговские пики под ожидаемыми углами рассеяния для ОЦК-решетки (см. рис. 3).

Когда небольшое количество ионов охлаждается лазером, они образуют кристаллические «кулоновские кластеры». Симметрия кластера зависит от формы внешних удерживающих полей. Интерактивное 3D-изображение некоторых кластеров можно найти здесь .