График Эрреры
| График Эрреры | |
|---|---|
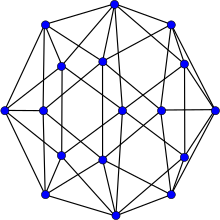 График Эрреры | |
| Назван в честь | Альфред Эррера |
| Вершины | 17 |
| Края | 45 |
| Радиус | 3 |
| Диаметр | 4 |
| Обхват | 3 |
| Автоморфизм | 20 ( Д 10 ) |
| Хроматическое число | 4 |
| Хроматический индекс | 6 |
| Характеристики | Планарный гамильтониан |
| Таблица графиков и параметров | |
В математической области теории графов граф Эрреры представляет собой граф с 17 вершинами и 45 ребрами . Альфред Эррера опубликовал его в 1921 году как контрпример к теоремы ошибочному доказательству Кемпе о четырех цветах ; [1] [2] назвал его в честь Эрреры Hutchinson & Wagon (1998) . [1]
Характеристики
[ редактировать ]Граф Эрреры плоский и имеет хроматическое число 4, хроматический индекс 6, радиус 3, диаметр 4 и обхват 3. Все его вершины имеют степень 5 или 6, и это 5 -связный граф и 5- реберно-связный граф. график .
Граф Эрреры не является вершинно-транзитивным графом , и его полная группа автоморфизмов изоморфна группе диэдра порядка 20, группе симметрий десятиугольника , включая как вращения, так и отражения.
Характеристический полином графа Эрреры равен .
Приложение к теореме о четырех цветах
[ редактировать ]
Теорема о четырех цветах утверждает, что вершины любого планарного графа можно раскрасить в четыре цвета, так что никакие две соседние вершины не будут иметь одинаковые цвета. Ошибочное доказательство было опубликовано в 1879 году Альфредом Кемпе , но его ошибочность была обнаружена к 1890 году. Теорема о четырех цветах не получила действительного доказательства до 1976 года.Доказательство Кемпе можно преобразовать в алгоритм раскраски плоских графов, что также ошибочно. Контрпримеры к его доказательству были найдены в 1890 и 1896 годах ( граф Пуссена ), а позже граф Фрича и граф Сойфера предоставили два меньших контрпримера. [3] Однако до работы Эрреры эти контрпримеры не показали, что весь алгоритм раскраски не работает. Скорее, они предположили, что все вершины графа, кроме одной, уже раскрашены.и показал, что метод Кемпе (который якобы должен был изменить раскраску, чтобы распространить ее на все графы) не сработал в этих предварительно раскрашенных случаях. С другой стороны, график Эрреры представляет собой контрпример всему методу Кемпе. Когда этот метод запускается на графе Эрреры, начиная с не окрашенных вершин, он может не найти правильную раскраску для всего графа. [1] Кроме того, в отличие от графа Пуссена, все вершины графа Эрреры имеют степень пять или более. Следовательно, на этом графе невозможно избежать проблемных случаев метода Кемпе путем выбора вершин меньшей степени.
На рисунке показан пример того, как доказательство Кемпе для этого графа может оказаться ошибочным. На рисунке смежности между областями этой карты образуют граф Эрреры, частично четырехцветный, а внешняя область неокрашенная. Ошибочное доказательство Кемпе следует за идеей расширения частичных раскрасок, подобных этой, путем перекрашивания цепочек Кемпе :связные подграфы, имеющие только два цвета. Любую такую цепочку можно перекрасить, сохранив правильность раскраски, поменяв местами два ее цвета во всех вершинах цепочки.Доказательство Кемпе имеет разные случаи в зависимости от того, имеет ли следующая раскрашиваемая вершина трех, четырех или пяти соседей, а также от того, как эти соседи окрашены. В показанном случае следующей окрашиваемой вершиной будет вершина, соответствующая внешней области карты.Эту область нельзя раскрасить напрямую, поскольку у нее уже есть соседи всех четырех разных цветов. Синие и желтые соседи соединены одной цепочкой Кемпе (показана пунктирными желтыми линиями на изображении), что не позволяет замене сделать их одновременно синими или желтыми и освободить цвет.Аналогично синие и зеленые соседи соединены еще одной цепочкой Кемпе (пунктирные зеленые линии). В таком случае доказательство Кемпе попытается одновременно поменять цвета на двух цепочках Кемпе: левой красно-желтой цепочке и правой красно-зеленой цепочке (пунктирные красные линии).Сине-зеленая цепочка блокирует левую красно-желтую цепочку от достижения правой части графика, а сине-желтая цепочка блокирует правую красно-зеленую цепочку от достижения левой части, поэтому казалось бы, что одновременная замена цветов на этих две цепи – безопасная операция.Но поскольку сине-желтая и сине-зеленая цепи пересекаются, а не остаются разделенными, в середине рисунка есть область, где могут встретиться красно-желтая и красно-зеленая цепи.Когда эти две цепочки встречаются посередине, одновременная замена приводит к тому, что соседние желтые и зеленые вершины в этой средней области (например, вершины, представленные верхними желтыми и зелеными областями на рисунке) становятся красными, создавая недопустимую окраску.
Приложения в химии
[ редактировать ]Химическая теория графов касается теоретико-графовой структуры молекул и других кластеров атомов. как сам граф Эрреры, так и его двойственный граф В этом контексте актуальны .
Атомы металлов, таких как золото, могут образовывать кластеры , в которых центральный атом окружен еще двенадцатью атомами, образуя структуру икосаэдра . Другой, более крупный тип кластера может быть образован путем объединения двух таких икосаэдрических кластеров, так что центральный атом каждого кластера становится одним из граничных атомов для другого кластера.Полученный кластер из 19 атомов имеет два внутренних атома (центры двух икосаэдров) и 17 атомов во внешней оболочке в соответствии с узором графа Эрреры. [4]
Двойственный граф графа Эрреры представляет собой фуллерен. [1] с 30 вершинами, обозначенными в химической литературе как С 30 (D 5 h ) [5] или F 30 (Д 5 ч ) [6] чтобы указать на его симметрию и отличить его от других 30-вершинных фуллеренов.Эта форма также играет центральную роль в построении фуллеренов более высокой размерности. [6]
Ссылки
[ редактировать ]- ^ Jump up to: а б с д Хатчинсон, Джоан ; Вагон, Стэн (1998), «Возвращение Кемпе», American Mathematical Monthly , 105 (2): 170–174, doi : 10.2307/2589650 , JSTOR 2589650 , MR 1605875 .
- ^ Эррера, А. (1921), О раскраске карт и некоторых вопросах анализа местности , докторская диссертация .
- ^ Гетнер, Эллен; Спрингер, Уильям М., II (2003), «Насколько ложно доказательство Кемпе теоремы о четырех цветах?», Труды тридцать четвертой Юго-восточной международной конференции по комбинаторике, теории графов и вычислениям, Congressus Numerantium , 164 : 159–175 , МР 2050581
{{citation}}: CS1 maint: несколько имен: список авторов ( ссылка ) . - ^ Майкл, Д.; Мингос, П. (2015), «Структурные структуры и закономерности связей в кластерах золота», Dalton Trans. , 44 (15): 6680–6695, doi : 10.1039/c5dt00253b , PMID 25710593 .
- ^ Матур, Ракеш Бехари; Сингх, Бхану Пратап; Панде, Шайладжа (2016), Углеродные наноматериалы: синтез, структура, свойства и применение , CRC Press, стр. 59, ISBN 9781498702119 .
- ^ Jump up to: а б Деза, Мишель ; Штогрин, Михаил (1999), «Трех-, четырех- и пятимерные фуллерены», Математический бюллетень Юго-Восточной Азии , 23 (1): 9–18, arXiv : math/9906035 , Bibcode : 1999math..... .6035D , МР 1810781 .



