Срок ведущего порядка
Членами ведущего порядка (или поправками ) в математическом уравнении , выражении или модели являются члены с наибольшим порядком величины . [1] [2] Размеры различных членов в уравнении(ях) будут меняться по мере изменения переменных , и, следовательно, то, какие члены являются ведущими, также может измениться.
Распространенный и эффективный способ упрощения и понимания широкого спектра сложных математических моделей состоит в том, чтобы исследовать, какие члены являются самыми большими (и, следовательно, наиболее важными) для определенных размеров переменных и параметров, и проанализировать поведение, вызываемое только этими членами ( считая другие меньшие члены пренебрежимо малыми). [3] [4] Это дает основное поведение – истинное поведение отличается от этого лишь небольшими отклонениями. Это основное поведение может быть достаточно хорошо отражено только членами строго ведущего порядка, или может быть решено, что следует включить также члены немного меньшего размера. В этом случае фраза « термины ведущего порядка» может использоваться неформально для обозначения всей этой группы терминов. Поведение, создаваемое только группой членов ведущего порядка, называется ведущего порядка поведением модели .
Базовый пример [ править ]
| х | 0.001 | 0.1 | 0.5 | 2 | 10 |
|---|---|---|---|---|---|
| х 3 | 0.000000001 | 0.001 | 0.125 | 8 | 1000 |
| 55x | 0.005 | 0.5 | 2.5 | 10 | 50 |
| 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| и | 0.105000001 | 0.601 | 2.725 | 18.1 | 1050.1 |
Рассмотрим уравнение y = x 3 + 5 х + 0,1. Для пяти различных значений x таблица показывает размеры четырех членов в этом уравнении и какие члены являются ведущими. По мере дальнейшего увеличения x члены главного порядка остаются равными x 3 и y , но по мере того, как x уменьшается, а затем становится все более и более отрицательным, порядок ведущих членов снова меняется.
Не существует строгого ограничения на то, когда два термина следует или не следует рассматривать как примерно одинаковые по порядку или величине. Одно из возможных эмпирических правил состоит в том, что два термина, которые отличаются друг от друга в пределах 10 (одного порядка), следует рассматривать как относящиеся примерно к одному и тому же порядку, а два термина, которые отличаются друг от друга в пределах 100 (два порядка величины). величины) друг друга не должны. Однако между ними находится серая зона, поэтому не существует фиксированных границ, где термины следует рассматривать как примерно ведущие, а где нет. Вместо этого термины то появляются, то исчезают по мере изменения переменных. Решение о том, имеют ли термины в модели ведущий порядок (или приблизительно ведущий порядок), а если нет, то достаточно ли они малы, чтобы их можно было считать незначительными (два разных вопроса), часто является предметом исследования и суждения, и будет зависят от контекста.
Поведение в порядке ведущего [ править ]
Уравнения только с одним членом ведущего порядка возможны, но редки. [ сомнительно – обсудить ] Например, уравнение 100 = 1 + 1 + 1 + ... + 1 (где правая часть содержит сто единиц). Для любой конкретной комбинации значений переменных и параметров уравнение обычно содержит как минимум два члена старшего порядка и другие члены более низкого порядка . В этом случае, если предположить, что члены низшего порядка и части членов ведущего порядка, имеющие тот же размер, что и члены низшего порядка (возможно, вторая или третья значащая цифра и далее), пренебрежимо малы, новое уравнение можно составить, отбросив все эти члены низшего порядка и части членов старшего порядка. Остальные члены образуют уравнение ведущего порядка или баланс ведущего порядка . [5] или доминирующий баланс , [6] [7] [8] и создание нового уравнения, включающего только эти члены, называется переводом уравнения в ведущий порядок . Решения этого нового уравнения называются решениями ведущего порядка. [9] [10] к исходному уравнению. Анализ поведения, заданного этим новым уравнением, дает поведение ведущего порядка. [11] [12] модели для этих значений переменных и параметров. Размер ошибки при таком приближении обычно примерно равен размеру наибольшего пренебрегаемого члена.
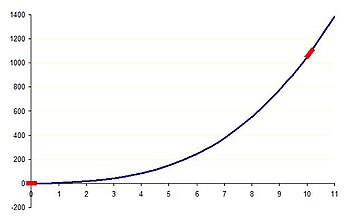
Предположим, мы хотим понять поведение ведущего порядка в приведенном выше примере.
- Когда x = 0,001, x 3 и члены 5 x могут считаться незначительными и отбрасываться вместе со всеми значениями в третьем десятичном знаке и далее в двух оставшихся членах. Это дает баланс лидирующего порядка y = 0,1. Таким образом, поведение этого уравнения в главном порядке при x=0,001 заключается в том, что y является постоянным.
- Аналогичным образом, когда x = 10, члены 5 x и 0,1 можно рассматривать как пренебрежимо малые и отбрасывать их вместе с любыми значениями третьей значащей цифры и далее в двух оставшихся членах. Это дает баланс ведущего порядка y = x 3 . Таким образом, поведение главного порядка этого уравнения при x=10 заключается в том, что y увеличивается кубически с x .
Таким образом, основное поведение y можно исследовать при любом значении x . Поведение ведущего порядка усложняется, когда в ведущем порядке находится больше терминов. При x=2 существует баланс главного порядка между кубической и линейной зависимостью y от x .
Обратите внимание, что это описание поиска балансов и поведения ведущих порядков дает лишь общее описание процесса – оно не является математически строгим.
Следующий за ведущим порядок [ править ]
Конечно, y не является на самом деле полностью постоянным при x = 0,001 – это всего лишь его основное поведение вблизи этой точки. Возможно, сохранение только членов ведущего порядка (или приблизительно ведущего порядка) и рассмотрение всех остальных меньших членов как незначительных недостаточно (например, при использовании модели для прогнозирования будущего), и поэтому это может быть необходимо. чтобы также сохранить набор следующих по величине членов. Их можно назвать условиями или поправками следующего за ведущим порядком (NLO). [13] [14] Следующий набор терминов после этого можно назвать терминами или исправлениями следующего за следующим за ведущим порядком (NNLO). [15]
Использование [ править ]
Согласованные асимптотические разложения [ править ]
Методы упрощения ведущего порядка используются в сочетании с методом согласованных асимптотических разложений , когда точным приближенным решением в каждой подобласти является решение ведущего порядка. [3] [16] [17]
уравнений Упрощение Стокса
Для конкретных сценариев течения жидкости (очень общие) уравнения Навье – Стокса можно значительно упростить, рассматривая только компоненты главного порядка. Например, уравнения потока Стокса . [18] А также уравнения теории смазки для тонких пленок .
дифференциальных уравнений с помощью машинного Упрощение обучения
Различные дифференциальные уравнения можно локально упростить, рассматривая только компоненты старшего порядка. Алгоритмы машинного обучения могут разделять данные моделирования или наблюдений на локализованные разделы с членами уравнений ведущего порядка для аэродинамики, динамики океана, опухолевого ангиогенеза и приложений синтетических данных. [19]
См. также [ править ]
- Оценка , алгебраическое обобщение «ведущего порядка».
Ссылки [ править ]
- ^ JKHunter, Асимптотический анализ и теория сингулярных возмущений , 2004. http://www.math.ucdavis.edu/~hunter/notes/asy.pdf
- ^ Конспекты курса Нью-Йоркского университета
- ↑ Перейти обратно: Перейти обратно: а б Митчелл, MJ; и др. (2010). «Модель растворения углекислого газа и кинетики карбонизации минералов» . Труды Королевского общества А. 466 (2117): 1265–1290. Бибкод : 2010RSPSA.466.1265M . дои : 10.1098/rspa.2009.0349 .
- ^ Вуллард, ХФ; и др. (2008). «Многомасштабная модель переноса растворенных веществ в канале с волнистыми стенками» (PDF) . Журнал инженерной математики . 64 (1): 25–48. Бибкод : 2009JEnMa..64...25W . дои : 10.1007/s10665-008-9239-x .
- ^ Штернберг, П.; Бернофф, Эй Джей (1998). «Возникновение сверхпроводимости в спадающих полях для общих областей» . Журнал математической физики . 39 (3): 1272–1284. Бибкод : 1998JMP....39.1272B . дои : 10.1063/1.532379 .
- ^ Саламон, ТР; и др. (1995). «Роль поверхностного натяжения в доминирующем балансе в сингулярности расширения матрицы» . Физика жидкостей . 7 (10): 2328–2344. Бибкод : 1995PhFl....7.2328S . дои : 10.1063/1.868746 . Архивировано из оригинала 8 июля 2013 г.
- ^ Горшков А.В.; и др. (2008). «Когерентное квантово-оптическое управление с субволновым разрешением». Письма о физических отзывах . 100 (9): 93005. arXiv : 0706.3879 . Бибкод : 2008PhRvL.100i3005G . doi : 10.1103/PhysRevLett.100.093005 . ПМИД 18352706 . S2CID 3789664 .
- ^ Линденберг, К .; и др. (1994). «Бинарные реакции, ограниченные диффузией: иерархия неклассических режимов для коррелированных начальных условий» (PDF) . Журнал физической химии . 98 (13): 3389–3397. дои : 10.1021/j100064a020 .
- ^ Женчиковский, П. (1988). «Матрица Кобаяши – Маскавы из решения главного порядка модели Фрича n -поколения». Физический обзор D . 38 (1): 332–336. Бибкод : 1988PhRvD..38..332Z . дои : 10.1103/PhysRevD.38.332 . ПМИД 9959017 .
- ^ Горовиц, GT; Цейтлин А.А. (1994). «Экстремальные черные дыры как точные струнные решения». Письма о физических отзывах . 73 (25): 3351–3354. arXiv : hep-th/9408040 . Бибкод : 1994PhRvL..73.3351H . дои : 10.1103/PhysRevLett.73.3351 . ПМИД 10057359 . S2CID 43551044 .
- ^ Хусейн, А. (1980). «Поведение главного порядка амплитуд двухфотонного рассеяния в КХД». Ядерная физика Б . 163 : 453–460. Бибкод : 1980НуФБ.163..453А . дои : 10.1016/0550-3213(80)90411-3 .
- ^ Крученский, М.; Оксман, Луизиана; Салдарриага, М. (1999). «Большое сжатие генерации космологической энтропии». Классическая и квантовая гравитация . 11 (9): 2317–2329. arXiv : gr-qc/9403024 . Бибкод : 1994CQGra..11.2317K . дои : 10.1088/0264-9381/11/9/013 . S2CID 13979794 .
- ^ Кэмпбелл, Дж.; Эллис, РК (2002). «Следующие за ведущими поправки к порядку образования струй W + 2 и Z + 2 на адронных коллайдерах». Физический обзор D . 65 (11): 113007. arXiv : hep-ph/0202176 . Бибкод : 2002PhRvD..65k3007C . дои : 10.1103/PhysRevD.65.113007 . S2CID 119355645 .
- ^ Катани, С.; Сеймур, Миннесота (1996). «Дипольный формализм для расчета сечений струи КХД в следующем за ведущим порядке». Буквы по физике Б. 378 (1): 287–301. arXiv : hep-ph/9602277 . Бибкод : 1996PhLB..378..287C . дои : 10.1016/0370-2693(96)00425-X . S2CID 15422325 .
- ^ Кидонакис, Н.; Фогт, Р. (2003). «Поправки мягкого глюона ближайшего к следующему порядку в гадророждении топ-кварков». Физический обзор D . 68 (11): 114014. arXiv : hep-ph/0308222 . Бибкод : 2003PhRvD..68k4014K . дои : 10.1103/PhysRevD.68.114014 . S2CID 5943465 .
- ^ Рубинштейн, BY; Писмен, Л.М. (1994). «Вихревое движение в пространственно-неоднородной консервативной модели Гинзбурга – Ландау» (PDF) . Физика D: Нелинейные явления . 78 (1): 1–10. Бибкод : 1994PhyD...78....1R . дои : 10.1016/0167-2789(94)00119-7 .
- ^ Кившарь, Ю.С.; и др. (1998). «Динамика оптических вихревых солитонов» (PDF) . Оптические коммуникации . 152 (1): 198–206. Бибкод : 1998OptCo.152..198K . дои : 10.1016/S0030-4018(98)00149-7 . Архивировано из оригинала (PDF) 21 апреля 2013 г. Проверено 31 октября 2012 г.
- ^ Заметки Корнельского университета
- ^ Кайзер, Брайан Э.; Саенс, Хуан А.; Зонневальд, Майке; Ливеску, Даниэль (2022). «Автоматизированная идентификация доминирующих физических процессов» . Инженерные применения искусственного интеллекта . 116 : 105496. дои : 10.1016/j.engappai.2022.105496 . S2CID 252957864 .