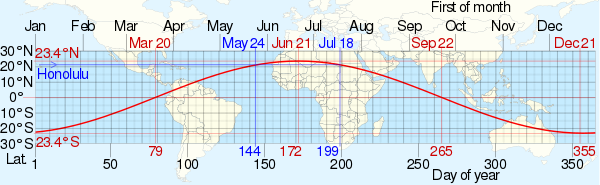
Зенитный угол Солнца

Зенитный угол Солнца — это зенитный угол Солнца , т. е . угол между солнечными лучами и вертикальным направлением . Это дополнение к высоте Солнца или высоте Солнца , которая представляет собой угол высоты или угол возвышения между солнечными лучами и горизонтальной плоскостью . ^[1]^[2] В солнечный полдень зенитный угол минимален и равен широте минус угол склонения Солнца . Это основа, с помощью которой древние мореплаватели путешествовали по океанам. ^[3]

Угол солнечного зенита обычно используется в сочетании с углом солнечного азимута для определения положения Солнца , наблюдаемого из данного места на поверхности Земли.

Формула

$\cos \theta _{s}=\sin \alpha _{s}=\sin \Phi \sin \delta +\cos \Phi \cos \delta \cos h$

где

$\theta _{s}$ зенитный угол Солнца
$\alpha _{s}$ — угол высоты Солнца , $\alpha _{s}=90^{\circ }-\theta _{s}$
$h$ - часовой угол по местному солнечному времени .
$\delta$ текущее склонение Солнца
$\Phi$ это местная широта .

Вывод формулы с использованием подсолнечной точки и векторного анализа

Хотя формулу можно вывести, применив закон косинуса к сферическому треугольнику зенит-полюс-Солнце, сферическая тригонометрия является относительно эзотерическим предметом.

Введя координаты подсолнечной точки и используя векторный анализ, формулу можно получить напрямую, не прибегая к использованию сферической тригонометрии. ^[4]

В геоцентрической декартовой системе координат Earth-centered Earth-Fixed ( ECEF ) пусть $(\phi _{s},\lambda _{s})$ и $(\phi _{o},\lambda _{o})$ быть широтой и долготой или координатами подсолнечной точки и точки наблюдателя, а затем направленными вверх единичными векторами в этих двух точках, $\mathbf {S}$ и $\mathbf {V} _{oz}$ , являются

$\mathbf {S} =\cos \phi _{s}\cos \lambda _{s}{\mathbf {i} }+\cos \phi _{s}\sin \lambda _{s}{\mathbf {j} }+\sin \phi _{s}{\mathbf {k} },$ $\mathbf {V} _{oz}=\cos \phi _{o}\cos \lambda _{o}{\mathbf {i} }+\cos \phi _{o}\sin \lambda _{o}{\mathbf {j} }+\sin \phi _{o}{\mathbf {k} }.$

где ${\mathbf {i} }$ , ${\mathbf {j} }$ и ${\mathbf {k} }$ – базисные векторы в системе координат ECEF.

Теперь косинус зенитного угла Солнца, $\theta _{s}$ , представляет собой просто скалярное произведение двух вышеуказанных векторов

$\cos \theta _{s}=\mathbf {S} \cdot \mathbf {V} _{oz}=\sin \phi _{o}\sin \phi _{s}+\cos \phi _{o}\cos \phi _{s}\cos(\lambda _{s}-\lambda _{o}).$

Обратите внимание, что $\phi _{s}$ то же самое, что $\delta$ , склонение Солнца и $\lambda _{s}-\lambda _{o}$ эквивалентно $-h$ , где $h$ часовой угол, определенный ранее. Таким образом, приведенный выше формат математически идентичен приведенному ранее.

Кроме того, ссылка. ^[4] также вывел формулу для угла азимута Солнца аналогичным образом, без использования сферической тригонометрии.

Минимум и максимум

В любом месте в любой день зенитный угол Солнца $\theta _{s}$ , достигает своего минимума, $\theta _{\text{min}}$ , в местный солнечный полдень, когда часовой угол $h=0$ , или $\lambda _{s}-\lambda _{o}=0$ , а именно, $\cos \theta _{\text{min}}=\cos(|\phi _{o}-\phi _{s}|)$ , или $\theta _{\text{min}}=|\phi _{o}-\phi _{s}|$ . Если $\theta _{\text{min}}>90^{\circ }$ , сейчас полярная ночь.

И в любом месте в любой день зенитный угол Солнца $\theta _{s}$ , достигает своего максимума, $\theta _{\text{max}}$ , в местную полночь, когда часовой угол $h=-180^{\circ }$ , или $\lambda _{s}-\lambda _{o}=-180^{\circ }$ , а именно, $\cos \theta _{\text{max}}=\cos(180^{\circ }-|\phi _{o}+\phi _{s}|)$ , или $\theta _{\text{max}}=180^{\circ }-|\phi _{o}+\phi _{s}|$ . Если $\theta _{\text{max}}<90^{\circ }$ , это полярный день.

Предостережения

Рассчитанные значения являются приблизительными из-за различия между общей/геодезической широтой и геоцентрической широтой . Однако эти два значения различаются менее чем на 12 угловых минут , что меньше видимого углового радиуса Солнца.

Формула также не учитывает влияние атмосферной рефракции . ^[5]

Приложения

Восход/Закат

Закат и восход солнца происходят (приблизительно), когда зенитный угол равен 90°, где часовой угол h ₀ удовлетворяет условию ^[2] $\cos h_{0}=-\tan \Phi \tan \delta .$

Точное время заката и восхода солнца происходит, когда кажется, что верхняя часть Солнца, преломленная атмосферой, находится на горизонте.

Альбедо

Взвешенный среднесуточный зенитный угол, используемый при вычислении местного альбедо Земли , определяется выражением ${\overline {\cos \theta _{s}}}={\frac {\displaystyle \int _{-h_{0}}^{h_{0}}Q\cos \theta _{s}\,{\text{d}}h}{\displaystyle \int _{-h_{0}}^{h_{0}}Q\,{\text{d}}h}}$ где Q — мгновенная освещенность . ^[2]

Краткое описание специальных ракурсов

Например, угол возвышения Солнца равен:

90°, если вы находитесь на экваторе, в день равноденствия, в солнечный час двенадцать
около 0° на закате или на восходе солнца
от −90° до 0° ночью (полночь)

Точный расчет дан по положению Солнца . Другие приближения существуют в других местах. ^[6]

Приблизительные даты подсолнечной точки в зависимости от широты, наложенные на карту мира, пример синим цветом обозначает полдень Лахайны в Гонолулу.

См. также

Ссылки

^ Джейкобсон, Марк З. (2005). Основы моделирования атмосферы (2-е изд.). Издательство Кембриджского университета . п. 317 . ISBN 0521548659 .
^ Jump up to: ^а ^б ^с Хартманн, Деннис Л. (1994). Глобальная физическая климатология . Академическая пресса . п. 30 . ISBN 0080571638 .
^ Бонан, Гордон (2005). Экологическая климатология: понятия и приложения . Издательство Кембриджского университета. п. 62. ИСБН 9781316425190 . Проверено 13 ноября 2019 г. .
^ Jump up to: ^а ^б Чжан Т., Стэкхаус П.В., Макферсон Б. и Миковиц Дж.К., 2021. Формула солнечного азимута, которая делает ненужным косвенное рассмотрение без ущерба для математической строгости: математическая установка, применение и расширение формулы, основанной на подсолнечной точке и функция atan2. Возобновляемая энергия, 172, 1333–1340. DOI: https://doi.org/10.1016/j.renene.2021.03.047.
^ Вульф, Гарольд М. (1968). «О вычислении углов возвышения Солнца и определении времени восхода и захода солнца». Технический меморандум НАСА, X-1646 . Вашингтон, округ Колумбия: 3.
^ ливиофлорес-га. «Уравнение, позволяющее узнать, где находится Солнце в данном месте в данную дату и время» . Проверено 9 марта 2013 г.

[1] Джейкобсон, Марк З. (2005). Основы моделирования атмосферы (2-е изд.). Издательство Кембриджского университета . п. 317 . ISBN 0521548659 .

[hartmann-2] Jump up to: ^а ^б ^с Хартманн, Деннис Л. (1994). Глобальная физическая климатология . Академическая пресса . п. 30 . ISBN 0080571638 .

[3] Бонан, Гордон (2005). Экологическая климатология: понятия и приложения . Издательство Кембриджского университета. п. 62. ИСБН 9781316425190 . Проверено 13 ноября 2019 г. .

[Zhangetal-4] Jump up to: ^а ^б Чжан Т., Стэкхаус П.В., Макферсон Б. и Миковиц Дж.К., 2021. Формула солнечного азимута, которая делает ненужным косвенное рассмотрение без ущерба для математической строгости: математическая установка, применение и расширение формулы, основанной на подсолнечной точке и функция atan2. Возобновляемая энергия, 172, 1333–1340. DOI: https://doi.org/10.1016/j.renene.2021.03.047.

[5] Вульф, Гарольд М. (1968). «О вычислении углов возвышения Солнца и определении времени восхода и захода солнца». Технический меморандум НАСА, X-1646 . Вашингтон, округ Колумбия: 3.

[6] ливиофлорес-га. «Уравнение, позволяющее узнать, где находится Солнце в данном месте в данную дату и время» . Проверено 9 марта 2013 г.

[1]

[2]

[3]

[4]

[5]

[6]