Часовой угол
Эта статья нуждается в дополнительных цитатах для проверки . ( апрель 2018 г. ) |
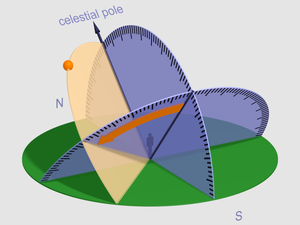
В астрономии и астрономической навигации часовой угол — это двугранный угол между плоскостью меридиана (содержащей ось Земли и зенит ) и часовым кругом (содержащим ось Земли и заданную точку интереса). [1]
В зависимости от применения оно может быть задано в градусах, времени или оборотах.Угол может быть выражен как отрицательный к востоку от плоскости меридиана и положительный к западу от плоскости меридиана или как положительный к западу от 0° до 360°. Угол может измеряться в градусах или во времени, при этом 24 час = 360° ровно.В астрономической навигации принято измерять в градусах на запад от нулевого меридиана ( часовой угол по Гринвичу , GHA ), от местного меридиана ( местный часовой угол , LHA ) или от первой точки Овна ( сидерический часовой угол , SHA ).
Часовой угол сочетается со склонением , чтобы полностью указать расположение точки на небесной сфере в экваториальной системе координат . [2]
Связь с прямым восхождением [ править ]
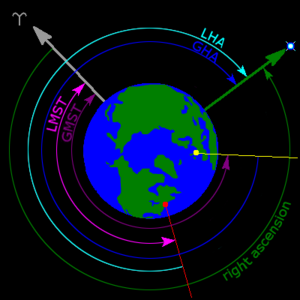
Предположим, что в этом примере день года — мартовское равноденствие, поэтому солнце лежит в направлении серой стрелки, тогда эта звезда взойдет около полуночи. Сразу после того, как наблюдатель достигает зеленой стрелки, наступает рассвет и затмевает видимость звезды примерно за шесть часов до ее заката на западном горизонте. Прямое восхождение звезды около 18. час
Местный часовой угол (LHA) объекта на небе наблюдателя равен
Отрицательные часовые углы (-180° < объект LHA <0°) указывают на то, что объект приближается к меридиану, положительные часовые углы (0° < объект LHA <180°) указывают на то, что объект удаляется от меридиана; нулевой часовой угол означает, что объект находится на меридиане.
Солнечный часовой угол [ править ]
При наблюдении Солнца с Земли солнечный часовой угол представляет собой выражение времени, выраженное в угловых измерениях, обычно в градусах, от солнечного полудня . В солнечный полдень часовой угол равен нулю градусов, при этом время до солнечного полудня выражается в отрицательных градусах, а местное время после солнечного полудня выражается в положительных градусах. Например, в 10:30 утра по местному кажущемуся времени часовой угол равен -22,5° (15° в час, умноженный на 1,5 часа до полудня). [4]
Косинус h часового угла (cos( ) ) используется для расчета зенитного угла Солнца . В солнечный полдень h = 0,000 , поэтому cos( h ) = 1 , а до и после солнечного полудня член cos(± h ) = одно и то же значение для утра (отрицательный часовой угол) или дня (положительный часовой угол), так что Солнце находится на одной высоте на небе в 11:00 и 13:00 по солнечному времени. [5]
Сидерический часовой угол [ править ]
Сидерический часовой угол (SHA) тела на небесной сфере — это его угловое расстояние к западу от мартовского равноденствия, обычно измеряемое в градусах. SHA звезды меняется менее чем на минуту дуги в год из-за прецессии , тогда как SHA планеты значительно меняется от ночи к ночи. SHA часто используется в астрономической навигации и навигационной астрономии, а значения публикуются в астрономических альманахах . [ нужна ссылка ]
См. также [ править ]
Примечания и ссылки [ править ]
- ^ Морской альманах Военно-морской обсерватории США (1992). П. Кеннет Зайдельманн (ред.). Пояснительное приложение к Астрономическому альманаху . Милл-Вэлли, Калифорния : Университетские научные книги. п. 729. ИСБН 0-935702-68-7 .
- ^ Пояснительное приложение (1992), с. 724.
- ^ Меус, Жан (1991). Астрономические алгоритмы . Willmann-Bell, Inc., Ричмонд, Вирджиния. п. 88. ИСБН 0-943396-35-2 .
- ^ Крайдер, Дж. Ф. (2007). «Применение солнечной энергии». Экологически сознательное производство альтернативной энергии . стр. 13–92. дои : 10.1002/9780470209738.ch2 . ISBN 9780470209738 .
- ^ Шовенгердт, РА (2007). «Модели оптического излучения». Дистанционное зондирование . стр. 45–88. дои : 10.1016/B978-012369407-2/50005-X . ISBN 9780123694072 .



