Агрегатная функция

В управлении базами данных агрегатная функция или функция агрегирования — это функция , в которой несколько значений обрабатываются вместе для формирования единой сводной статистики .

Общие агрегатные функции включают в себя:

Другие включают:

Nanmean (означает игнорирование значений NaN, также известных как «ноль» или «ноль»)
стандартное отклонение

Формально агрегатная функция принимает на вход набор , мультимножество ) или список из некоторой входной области $I$ и выводит элемент выходной области $O.$ ( мешок ^[1] Входные и выходные домены могут быть одинаковыми, например, для SUM, или может быть другим, например, для COUNT.

Агрегатные функции обычно встречаются во многих языках программирования , в электронных таблицах и в реляционной алгебре .

The listagg функция, как определено в SQL:2016 . стандарте ^[2]объединяет данные из нескольких строк в одну объединенную строку.

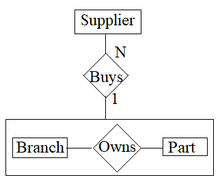
На диаграмме отношений сущностей агрегация представлена, как показано на рисунке 1, с прямоугольником вокруг связи и ее сущностей, что указывает на то, что она рассматривается как агрегированная сущность. ^[3]

Разложимые агрегатные функции [ править ]

Агрегатные функции представляют собой узкое место , поскольку потенциально требуют наличия всех входных значений одновременно. В распределенных вычислениях желательно разделить такие вычисления на более мелкие части и распределить работу, обычно вычисляя параллельно , с помощью алгоритма «разделяй и властвуй» .

Некоторые агрегатные функции можно вычислить путем вычисления агрегата для подмножеств и последующего агрегирования этих агрегатов; примеры включают в себя COUNT, MAX, MIN, и SUM. В других случаях агрегат можно вычислить путем вычисления вспомогательных чисел для подмножеств, объединения этих вспомогательных чисел и, наконец, вычисления общего числа в конце; примеры включают в себя AVERAGE (отслеживание суммы и количества, деление в конце) и RANGE (отслеживание максимума и минимума, вычитание в конце). В других случаях агрегат невозможно вычислить без анализа всего набора сразу, хотя в некоторых случаях аппроксимации могут быть распределены; примеры включают в себя DISTINCT COUNT ( Задача о подсчете различных ), MEDIAN, и MODE.

Такие функции называются разложимыми функциями агрегирования. ^[4] или разложимые агрегатные функции . Простейшие можно назвать саморазлагаемыми функциями агрегирования , которые определяются как такие функции $f$ , что существует оператор слияния. $\diamond$ такой, что

f(X\uplus Y)=f(X)\diamond f(Y)

где $\uplus$ есть объединение мультимножеств (см. моноидный гомоморфизм ).

Например, SUM:

\operatorname {SUM} ({x})=x

, для синглтона;

\operatorname {SUM} (X\uplus Y)=\operatorname {SUM} (X)+\operatorname {SUM} (Y)

, что означает слияние

\diamond

это просто дополнение.

COUNT:

\operatorname {COUNT} ({x})=1

,

\operatorname {COUNT} (X\uplus Y)=\operatorname {COUNT} (X)+\operatorname {COUNT} (Y)

.

MAX:

\operatorname {MAX} ({x})=x

,

\operatorname {MAX} (X\uplus Y)=\max {\bigl (}\operatorname {MAX} (X),\operatorname {MAX} (Y){\bigr )}

.

MIN:

{\textstyle \operatorname {MIN} ({x})=x}

, ^[2]

\operatorname {MIN} (X\uplus Y)=\min {\bigl (}\operatorname {MIN} (X),\operatorname {MIN} (Y){\bigr )}

.

Обратите внимание, что саморазлагаемые функции агрегирования можно комбинировать (формально, взяв произведение), применяя их по отдельности, так, например, можно вычислить как SUM и COUNT одновременно, отслеживая два номера.

В более общем смысле, можно определить разложимую агрегирующую функцию $f$ как функцию, которую можно выразить как композицию конечной функции $g$ и саморазложимой агрегирующей функции $h$ , $f=g\circ h,f(X)=g(h(X))$ . Например, AVERAGE= SUM/ COUNT и RANGE= MAX− MIN.

В среде MapReduce эти шаги известны как InitialReduce (значение для отдельной записи/одиночного набора), Объединение (двоичное слияние двух агрегатов) и FinalReduce (конечная функция для вспомогательных значений). ^[5] и перемещение разлагаемой агрегации перед фазой перемешивания, известной как шаг InitialReduce, ^[6]

Разлагаемые функции агрегации важны для онлайн-аналитической обработки (OLAP), поскольку они позволяют вычислять запросы агрегации на основе предварительно вычисленных результатов в кубе OLAP , а не на основе базовых данных. ^[7] Например, легко поддерживать COUNT, MAX, MIN, и SUM в OLAP, поскольку их можно вычислить для каждой ячейки куба OLAP, а затем суммировать («свернуть»), но это трудно поддерживать MEDIAN, поскольку его необходимо вычислять для каждого представления отдельно.

Другие разложимые агрегатные функции [ править ]

Для расчета среднего и стандартного отклонения на основе совокупных данных необходимо иметь в наличии для каждой группы: сумму значений (Σx _i = SUM(x)), количество значений (N=COUNT(x)) и сумма квадратов значений (Σx _i²=СУММ(х ²)) каждой группы. ^[8]

AVG:

\operatorname {AVG} (X\uplus Y)={\bigl (}\operatorname {AVG} (X)*\operatorname {COUNT} (X)+\operatorname {AVG} (Y)*\operatorname {COUNT} (Y){\bigr )}/{\bigl (}\operatorname {COUNT} (X)+\operatorname {COUNT} (Y){\bigr )}

или

\operatorname {AVG} (X\uplus Y)={\bigl (}\operatorname {SUM} (X)+\operatorname {SUM} (Y){\bigr )}/{\bigl (}\operatorname {COUNT} (X)+\operatorname {COUNT} (Y){\bigr )}

или, только если COUNT(X)=COUNT(Y)

\operatorname {AVG} (X\uplus Y)={\bigl (}\operatorname {AVG} (X)+\operatorname {AVG} (Y){\bigr )}/2

SUM(x²):Сумма квадратов значений важна для расчета стандартного отклонения групп.

\operatorname {SUM} (X^{2}\uplus Y^{2})=\operatorname {SUM} (X^{2})+\operatorname {SUM} (Y^{2})

STDDEV:
Для конечной популяции с равными вероятностями во всех точках имеем ^[9]^{[ циклическая ссылка ]}

\operatorname {STDDEV} (X)=s(x)={\sqrt {{\frac {1}{N}}\sum _{i=1}^{N}(x_{i}-{\overline {x}})^{2}}}={\sqrt {{\frac {1}{N}}\left(\sum _{i=1}^{N}x_{i}^{2}\right)-({\overline {x}})^{2}}}={\sqrt {\operatorname {SUM} (x^{2})/\operatorname {COUNT} (x)-\operatorname {AVG} (x)^{2}}}

Это означает, что стандартное отклонение равно квадратному корню из разницы между средним значением квадратов значений и квадратом среднего значения.

\operatorname {STDDEV} (X\uplus Y)={\sqrt {\operatorname {SUM} (X^{2}\uplus Y^{2})/\operatorname {COUNT} (X\uplus Y)-\operatorname {AVG} (X\uplus Y)^{2}}}

\operatorname {STDDEV} (X\uplus Y)={\sqrt {{\bigl (}\operatorname {SUM} (X^{2})+\operatorname {SUM} (Y^{2}){\bigr )}/{\bigl (}\operatorname {COUNT} (X)+\operatorname {COUNT} (Y){\bigr )}-{\bigl (}(\operatorname {SUM} (X)+\operatorname {SUM} (Y))/(\operatorname {COUNT} (X)+\operatorname {COUNT} (Y)){\bigr )}^{2}}}

См. также [ править ]

Ссылки [ править ]

^ Иисус, Бакеро и Алмейда, 2011 , 2 Определение проблемы, стр. 1-2. 3.
^ Jump up to: Перейти обратно: ^а ^б Винанд, Маркус (15 мая 2017 г.). «Важные новости в сфере баз данных: новый стандарт SQL, облачные войны и ACIDRain (весна 2017 г.)» . ДЗона. Архивировано из оригинала 27 мая 2017 г. Проверено 10 июня 2017 г. В декабре 2016 года ISO выпустила новую версию стандарта SQL. В нем представлены новые функции, такие как сопоставление шаблонов строк, listagg, форматирование даты и времени и поддержка JSON.
^ Эльмасри, Рамез (2016). Основы систем баз данных . Шам Навате (Седьмое изд.). Хобокен, Нью-Джерси. п. 133. ИСБН 978-0-13-397077-7 . OCLC 913842106 . {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
^ Иисус, Бакеро и Алмейда 2011 , 2.1 Разложимые функции, стр. 3–4.
^ Ю, Гунда и Айсард 2009 , 2. Распределенная агрегация, стр. 2–4.
^ Ю, Гунда и Айсард 2009 , 2. Распределенная агрегация, с. 1.
^ Чжан 2017 , с. 1.
^ Оскар Бонилья, MBA.
^ Стандартное отклонение # Тождества и математические свойства

Литература [ править ]

Грабиш, Мишель; Маришаль, Жан-Люк; Месиар, Радко; Пап, Эндре (2009). Функции агрегирования . Энциклопедия математики и ее приложений. Том. 127. Кембридж: Издательство Кембриджского университета . ISBN 978-0-521-51926-7 . Збл 1196.00002 .
Агрегатные функции Oracle: примеры MAX, MIN, COUNT, SUM, AVG

Ю, Юань; Гунда, Прадип Кумар; Айсард, Майкл (2009). Распределенная агрегация для параллельных вычислений: интерфейсы и реализации . 22-й симпозиум ACM SIGOPS по принципам операционных систем. АКМ . стр. 247–260. дои : 10.1145/1629575.1629600 .
Господи, Павел; Бакеро, Карлос; Алмейда, Пауло Сержиу (2011). «Обзор алгоритмов агрегирования распределенных данных». arXiv : 1110.0725 [ cs.DC ].
Чжан, Чао (2017). Симметричная и асимметричная агрегатная функция в массово-параллельных вычислениях (технический отчет).

Внешние ссылки [ править ]

Агрегатные функции (Transact-SQL)

[FOOTNOTEJesusBaqueroAlmeida20112_Problem_Definition,_pp._3-1] Иисус, Бакеро и Алмейда, 2011 , 2 Определение проблемы, стр. 1-2. 3.

[:0-2] Jump up to: Перейти обратно: ^а ^б Винанд, Маркус (15 мая 2017 г.). «Важные новости в сфере баз данных: новый стандарт SQL, облачные войны и ACIDRain (весна 2017 г.)» . ДЗона. Архивировано из оригинала 27 мая 2017 г. Проверено 10 июня 2017 г. В декабре 2016 года ISO выпустила новую версию стандарта SQL. В нем представлены новые функции, такие как сопоставление шаблонов строк, listagg, форматирование даты и времени и поддержка JSON.

[3] Эльмасри, Рамез (2016). Основы систем баз данных . Шам Навате (Седьмое изд.). Хобокен, Нью-Джерси. п. 133. ИСБН 978-0-13-397077-7 . OCLC 913842106 . {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )

[FOOTNOTEJesusBaqueroAlmeida20112.1_Decomposable_functions,_pp._3–4-4] Иисус, Бакеро и Алмейда 2011 , 2.1 Разложимые функции, стр. 3–4.

[FOOTNOTEYuGundaIsard20092._Distributed_Aggregation,_pp._2–4-5] Ю, Гунда и Айсард 2009 , 2. Распределенная агрегация, стр. 2–4.

[FOOTNOTEYuGundaIsard20092._Distributed_Aggregation,_p._1-6] Ю, Гунда и Айсард 2009 , 2. Распределенная агрегация, с. 1.

[FOOTNOTEZhang20171-7] Чжан 2017 , с. 1.

[8] Оскар Бонилья, MBA.

[9] Стандартное отклонение # Тождества и математические свойства

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]