Батчерная сортировка слиянием нечет-чет

Батчерная сортировка слиянием нечет-чет

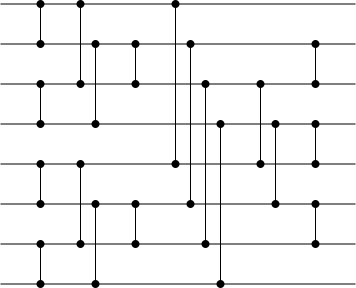Визуализация сети сортировки слиянием нечет-чет с восемью входами
Сорт	Алгоритм сортировки
Структура данных	Множество
Худшая производительность	$O(\log ^{2}(n))$ параллельное время
Лучшая производительность	$O(\log ^{2}(n))$ параллельное время
Средняя производительность	$O(\log ^{2}(n))$ параллельное время
Наихудшая пространственная сложность	$O(n\log ^{2}(n))$ непараллельное время
Оптимальный	Нет

Нечетно-четная сортировка слиянием Бэтчера — это общая конструкция, разработанная Кеном Бэтчером для сортировки сетей размера O( n (log n ) ² ) и глубина O((log n ) ² ), где n — количество элементов, подлежащих сортировке. Хотя он и не является асимптотически оптимальным, Кнут пришел к выводу в 1998 году относительно сети AKS , что «метод Бэтчера намного лучше, если только n не превышает общий объем памяти всех компьютеров на земле!»

Его популяризирует вторая книга GPU Gems , как простой способ достаточно эффективной сортировки на оборудовании для обработки графики.

Псевдокод

Возможны различные рекурсивные и итеративные схемы расчета индексов сравниваемых и сортируемых элементов. Это один из итеративных методов создания индексов для сортировки n элементов:

# note: the input sequence is indexed from 0 to (n-1)
for p = 1, 2, 4, 8, ... # as long as p < n
  for k = p, p/2, p/4, p/8, ... # as long as k >= 1
    for j = mod(k,p) to (n-1-k) with a step size of 2k
      for i = 0 to min(k-1, n-j-k-1) with a step size of 1
        if floor((i+j) / (p*2)) == floor((i+j+k) / (p*2))
          compare and sort elements (i+j) and (i+j+k)

Также возможен нерекурсивный расчет индекса узла-партнера.

См. также

• Битонический сортировщик
• Попарная сортировочная сеть

Внешние ссылки

• Сортировка слиянием «нечет-чет» на сайте hs-flensburg.de
• Генератор сети сортировки слиянием нечетно-четного Генератор сети сортировки слиянием на основе нечетно-четного от Interactive Batcher.