Шайба Бельвиля

Шайба Бельвиля , также известная как пружина с коническим диском , ^[1] коническая пружинная шайба , ^[2] Дисковая пружина , тарельчатая пружина или тарельчатая пружинная шайба представляет собой коническую оболочку, которая может нагружаться вдоль своей оси статически или динамически. Шайба Бельвиля представляет собой пружину, имеющую форму шайбы . Именно форма конуса усеченного придает шайбе характерную пружину.

Название «Бельвиль» происходит от изобретателя Жюльена Бельвиля , который в Дюнкерке , Франция, в 1867 году запатентовал конструкцию пружины, которая уже содержала принцип тарельчатой пружины. ^[1]^[3] Настоящий изобретатель шайб Бельвиля неизвестен.

За прошедшие годы было разработано множество профилей тарельчатых пружин. На сегодняшний день наиболее распространенными являются профили с или безконтактные лыски, в то время как некоторые другие профили, такие как тарельчатые пружины с трапециевидным поперечным сечением, потеряли значение.

Особенности и использование

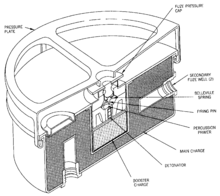
В различных областях, если они используются в качестве пружин или для приложения гибкой предварительной нагрузки к болтовому соединению или подшипнику, тарельчатые шайбы могут использоваться как одна пружина или как пакет. В пакете пружин тарельчатые пружины могут быть уложены в одинаковой или попеременной ориентации, и, конечно же, можно штабелировать пакеты из нескольких пружин, уложенных в одном направлении.

Дисковые пружины обладают рядом преимущественных свойств по сравнению с другими типами пружин: ^[4]

Очень большие нагрузки могут выдерживаться при небольшом монтажном пространстве.
Благодаря практически неограниченному количеству возможных комбинаций отдельных тарельчатых пружин характеристическую кривую и длину стойки можно дополнительно варьировать в дополнительных пределах.
Высокий срок службы при динамической нагрузке, если пружина правильно подобрана.
При условии, что допустимое напряжение не превышено, недопустимой релаксации не происходит.
При соответствующем расположении можно достичь большого эффекта демпфирования (высокого гистерезиса).
Поскольку пружины имеют кольцевую форму, передача усилия абсолютно концентрическая.

Благодаря этим выгодным свойствам тарельчатые шайбы сегодня используются во многих областях, некоторые примеры приведены ниже.

В военной промышленности тарельчатые пружины используются, например, в ряде мин, например, в американских М19 , М15 , М14 , М1 и шведских Трет-Ми.59. Цель (человек или транспортное средство) оказывает давление на тарельчатую пружину, в результате чего она превышает порог срабатывания и переворачивает соседний ударник вниз, образуя ударный детонатор , запуская как его, так и окружающий ускорительный заряд и основное взрывчатое вещество.

Шайбы Бельвиля использовались в качестве возвратных пружин в артиллерийских орудиях , одним из примеров является линейка французских морских/прибрежных пушек Кане конца 1800-х годов (75 мм, 120 мм, 152 мм).

Некоторые производители винтовок с продольно-скользящим затвором используют пакеты тарельчатых шайб в затворе вместо более традиционной пружины для освобождения ударника, поскольку они сокращают время между срабатыванием спускового крючка и ударом ударника по патрону. ^[5]

Тарельчатые шайбы без зубцов, которые могут повредить зажимную поверхность, не обладают значительной фиксирующей способностью при использовании болтов. ^[6]

На самолетах (обычно экспериментальных) с деревянными винтами тарельчатые шайбы, используемые на крепежных болтах, могут быть полезны в качестве индикатора набухания или усадки древесины. Затягивая соответствующие болты, чтобы обеспечить определенный зазор между наборами шайб, расположенных «верхними концами» друг к другу, изменение относительного содержания влаги в древесине гребного винта приведет к изменению зазоров, которое часто достаточно велико, чтобы его можно было обнаружить. визуально. Поскольку баланс винта зависит от одинакового веса лопастей, радикальная разница в зазорах шайб может указывать на разницу в содержании влаги – и, следовательно, в весе – в соседних лопастях.

В авиационной и автомобильной промышленности (в том числе Формулы-1) в автомобилях ^[7]^{[ нужен лучший источник ]}) дисковые пружины используются в качестве виброгасящих элементов из-за возможности их чрезвычайно детальной настройки. В самолетах серии Cirrus SR2x используется тарельчатая шайба для гашения колебаний передней стойки шасси (или «шимми»). ^[8]

В строительной отрасли Японии комплекты тарельчатых пружин использовались под зданиями в качестве демпферов вибраций при землетрясениях. ^[9]

Шайбы Бельвиля используются в некоторых регуляторах подачи воздуха высокого давления, например, в пейнтбольных маркерах и воздушных баллонах.

Укладка

Несколько тарельчатых шайб могут быть установлены друг на друга для изменения жесткости пружины (или жесткости пружины) или величины отклонения . Укладка в одном направлении параллельно добавит жесткость пружины, создавая более жесткое соединение (с тем же прогибом). Укладка в переменном направлении аналогична последовательному добавлению обычных пружин, что приводит к снижению жесткости пружины и большему отклонению. Смешивание и согласование направлений позволяют получить определенную жесткость пружины и прогибающую способность.

Обычно, если n тарельчатых пружин сложены параллельно (в одном и том же направлении), выдерживая нагрузку, прогиб всей стопки равен прогибу одной тарельчатой пружины, деленному на n , тогда для получения такого же прогиба одного диска Прикладываемая пружина нагрузка должна быть в n раз больше, чем у одной тарельчатой пружины. С другой стороны, если n шайб сложены последовательно (лицом в разных направлениях), выдерживая нагрузку, прогиб будет в n раз больше, чем у одной шайбы, в то время как нагрузка должна быть приложена ко всей стопке, чтобы получить такое же отклонение одной шайбы. Дисковая пружина должна представлять собой одну тарельчатую пружину, разделенную на n .

Вопросы производительности

В параллельном пакете возникает гистерезис (потери нагрузки) из-за трения между пружинами. Потери на гистерезис могут быть выгодны в некоторых системах из-за дополнительного демпфирования и рассеяния энергии вибрации. Эти потери из-за трения можно рассчитать с помощью методов гистерезиса. В идеале параллельно следует располагать не более 4 пружин. Если требуется большая нагрузка, необходимо увеличить коэффициент запаса прочности, чтобы компенсировать потерю нагрузки из-за трения. Потери на трение не являются такой уж серьезной проблемой при серийных сборках.

В последовательном пакете прогиб не совсем пропорционален количеству пружин. Это происходит из-за эффекта нижнего предела , когда пружины сжимаются до плоского состояния, поскольку площадь контактной поверхности увеличивается, когда пружина отклоняется более чем на 95%. Это уменьшит плечо момента, и пружина будет оказывать большее сопротивление. Гистерезис можно использовать для расчета прогнозируемых отклонений в последовательном пакете. Количество пружин, используемых в последовательном пакете, не является такой большой проблемой, как в параллельных пакетах, даже если, как правило, высота пакета не должна превышать внешний диаметр тарельчатой пружины более чем в три раза. Если невозможно избежать более длинной стопки, ее следует разделить на 2 или, возможно, 3 частичных стопки с помощью подходящих шайб. Эти шайбы должны направляться как можно точнее.

Как было сказано ранее, тарельчатые шайбы полезны для регулировки, поскольку их можно менять местами разной толщины, и их можно настроить так, чтобы обеспечить практически бесконечную настройку жесткости пружины, заполняя при этом лишь небольшую часть ящика с инструментами технического специалиста. Они идеальны в ситуациях, когда требуется большая сила пружины с минимальной свободной длиной и сжатием до достижения солидной высоты. Однако недостатком является вес, и их ход сильно ограничен по сравнению с обычной винтовой пружиной, когда свободная длина не является проблемой.

Волнистая шайба также действует как пружина, но волнистые шайбы сопоставимого размера не создают такой большой силы, как тарельчатые шайбы, и их нельзя устанавливать последовательно.

Тарельчатые пружины с контактными плоскостями и уменьшенной толщиной

Для тарельчатых пружин толщиной более 6,0 мм стандарт DIN 2093 в дополнение к закругленным углам предписывает небольшие контактные поверхности в точках I и III (т.е. в точке приложения нагрузки и в точке, где нагрузка касается земли). Эти контактные лыски улучшают определение точки приложения нагрузки и, особенно для пакетов пружин, уменьшают трение на направляющем стержне. Результатом является значительное уменьшение длины плеча рычага и соответствующее увеличение нагрузки пружины. Это, в свою очередь, компенсируется уменьшением толщины пружины.

Приведенная толщина определяется в соответствии со следующими условиями: ^[4]

Общая высота остается неизменной.
Ширина контактных площадок (то есть ширина кольцевого пространства) должна составлять примерно 1/150 наружного диаметра.
Нагрузка, прикладываемая к пружине уменьшенной толщины для получения прогиба, равного 75 % свободной высоты (неуменьшенной пружины), должна быть такой же, как и у неуменьшенной пружины.

Поскольку общая высота не уменьшается, пружины с уменьшенной толщиной неизбежно имеют увеличенный угол боковой поверхности и большую высоту конуса, чем пружины того же номинального размера без уменьшенной толщины. ^[4] Поэтому характеристическая кривая изменяется и становится совершенно другой.

Расчет

Начиная с 1936 г., когда Ж. О. Альмен и А. Ласло опубликовали упрощенную методику расчета, ^[10] Всегда появлялись более точные и сложные методы для включения в расчеты тарельчатых пружин с лысками контакта и уменьшенной толщиной. Итак, хотя сегодня существуют более точные методы расчета, ^[11] Наиболее часто используются простые и удобные формулы DIN 2092, поскольку для стандартных размеров они дают значения, которые хорошо соответствуют результатам измерений.

Учитывая тарельчатую шайбу наружного диаметра ${D_{e}}$ , внутренний диаметр ${D_{i}}$ , высота ${l}$ и толщина ${t}$ , где ${h_{0}}$ - свободная высота, то есть разница между высотой и толщиной, получаются следующие коэффициенты:

\delta ={\frac {D_{e}}{D_{i}}}

{C_{1}}={\frac {\left({\frac {t'}{t}}\right)^{2}}{\left({\frac {1}{4}}\cdot {\frac {l}{t}}-{\frac {t'}{t}}+{\frac {3}{4}}\right)\cdot {\left({\frac {5}{8}}\cdot {\frac {l}{t}}-{\frac {t'}{t}}+{\frac {3}{8}}\right)}}}

{C_{2}}={\frac {C_{1}}{\left({\frac {t'}{t}}\right)^{3}}}\cdot \left[{\frac {5}{32}}\cdot \left({\frac {l}{t}}-1\right)^{2}+1\right]

{K_{4}}={\sqrt {-{\frac {C_{1}}{2}}+{\sqrt {\left({\frac {C_{1}}{2}}\right)^{2}+C_{2}}}}}

Уравнение для расчета нагрузки, приложенной к одной дисковой пружине для получения прогиба ${s}$ является: ^[12]

F={\frac {4E}{1-\mu ^{2}}}\cdot {\frac {t^{4}}{K_{1}-{D_{e}}^{2}}}\cdot {K_{4}}^{2}\cdot {\frac {s}{t}}\cdot \left[{K_{4}}^{2}\cdot \left({\frac {h_{0}}{t}}-{\frac {s}{t}}\right)\cdot \left({\frac {h_{0}}{t}}-{\frac {s}{2t}}\right)+1\right]

Обратите внимание, что для тарельчатых пружин постоянной толщины ${t'}$ равно ${t}$ и, следовательно, ${K_{4}}$ это 1.

Что касается тарельчатых пружин с контактными плоскостями и уменьшенной толщиной, следует отметить, что в статье, опубликованной в июле 2013 года, показано, что ${K_{4}}$ Уравнение, определенное в стандартных нормах, неверно, так как в результате каждая уменьшенная толщина будет считаться правильной, а это, конечно, невозможно. Как написано в той статье ${K_{4}}$ следует заменить новым коэффициентом, ${R_{d}}$ , что зависит не только от ${\frac {t'}{t}}$ соотношение, но и от боковых углов пружины. ^[13]

Жесткость пружины (или жесткость пружины) определяется как:

{k}={\frac {dF}{ds}}

Если игнорировать эффекты трения и опускания, жесткость пружины стопки одинаковых тарельчатых шайб можно быстро приблизительно определить. Считая от одного конца стопки, группируйте по количеству соседних параллельно шайб. Например, в стопке шайб справа группировка 2-3-1-2, потому что параллельно идет группа из 2 шайб, затем группа из 3, затем одна шайба, затем еще группа из 2 шайб. .

Общий коэффициент пружины составляет:

K={\frac {k}{\sum _{i=1}^{g}{\frac {1}{n_{i}}}}}

K={\frac {k}{{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{1}}+{\frac {1}{2}}}}

K={\frac {3}{7}}\cdot {k}

Где

$n_{i}$ = количество шайб в i-й группе
${g}$ = количество групп
${k}$ = жесткость пружины одной шайбы

Таким образом, стопка 2-3-1-2 (или, поскольку сложение коммутативно, стопка 3-2-2-1) дает жесткость пружины 3/7 от жесткости одиночной шайбы. Эти самые 8 шайб можно расположить по схеме 3-3-2 ( $K={\frac {6}{7}}\cdot k$ ), конфигурация 4-4 ( $K=2\cdot k$ ), конфигурация 2-2-2-2 ( $K={\frac {1}{2}}\cdot k$ ) и различные другие конфигурации. Количество уникальных способов сложения ${n}$ шайб определяется целочисленной статистической суммой p ( n ) и быстро увеличивается с увеличением ${n}$ , что позволяет точно настроить жесткость пружины. Однако каждая конфигурация будет иметь разную длину, что в большинстве случаев требует использования прокладок .

Стандарты

DIN EN 16983 ранее DIN 2092 — Тарельчатые пружины — Расчет
DIN EN 16984 ранее DIN 2093 — Тарельчатые пружины. Характеристики производства и качества ^[14]
DIN 6796 — Шайбы пружинные конические для болтовых соединений. ^[2]

Ссылки

^ Jump up to: ^а ^б Шигли, Джозеф Эдвард; Мишке, Чарльз Р.; Браун, Томас Х. (2004), Стандартное руководство по проектированию машин (3-е изд.), McGraw-Hill Professional, стр. 640, ISBN 978-0-07-144164-3 .
^ Jump up to: ^а ^б Смит, Кэрролл (1990), Справочник Кэрролла Смита по гайкам, болтам, крепежу и сантехнике , MotorBooks/MBI Publishing Company, стр. 116, ISBN 0-87938-406-9 . ^{[ постоянная мертвая ссылка ]}
^ Бхандари, В.Б. (2010), Проектирование элементов машин (3-е изд.), Тата МакГроу-Хилл, стр. 441, ISBN 978-0-07-068179-8 .
^ Jump up to: ^а ^б ^с Справочник Шнорра , Шнорр, 2016 г., заархивировано из оригинала 3 октября 2016 г. , получено 4 октября 2016 г.
^ Actionclear Современные винтовки
^ Барретт, Ричард Т. (март 1990 г.). «Руководство по проектированию крепежа» (PDF) .
^ Инфинити Ред Булл РБ10 Рено
^ Руководство по техническому обслуживанию самолетов Cirrus (PDF) , Cirrus Aircraft , 2014 г., стр. 32, 34, заархивировано из оригинала (PDF) 3 октября 2016 г. , получено 4 октября 2016 г.
^ Накамура, Такаши; Сузуки, Тецуо; Нобата, Арихиде (1998), Исследование характеристик реакции на землетрясение здания с изолированным основанием с использованием фрикционных демпферов с коническими дисковыми пружинами (PDF) , Материалы 10-го симпозиума по сейсмостойкой инженерии, стр. 2901–2906.
^ Алмен, Дж.О.; Ласло, А. (1936), Дисковая пружина однородного сечения , ASME 58, стр. 305–314.
^ Курти, Грациано; Орландо, М. (1979), Новый расчет конических кольцевых дисковых пружин , Wire (28) 5, стр. 199–204.
^ DIN 2092: Тарельчатые пружины. Расчет , DIN, 2006 г.
^ Феррари, Джаммарко (2013), «Новый метод расчета тарельчатых пружин с контактными плоскостями и уменьшенной толщиной» , Международный журнал производства, материалов и машиностроения , 3 (2), IJMMME 3 (2): 63–73, дои : 10.4018/ijmmme.2013040105
^ «Продукты» . Архивировано из оригинала 21 июня 2020 г.

[shigley-1] Jump up to: ^а ^б Шигли, Джозеф Эдвард; Мишке, Чарльз Р.; Браун, Томас Х. (2004), Стандартное руководство по проектированию машин (3-е изд.), McGraw-Hill Professional, стр. 640, ISBN 978-0-07-144164-3 .

[smith-2] Jump up to: ^а ^б Смит, Кэрролл (1990), Справочник Кэрролла Смита по гайкам, болтам, крепежу и сантехнике , MotorBooks/MBI Publishing Company, стр. 116, ISBN 0-87938-406-9 . ^{[ постоянная мертвая ссылка ]}

[Bhandari-3] Бхандари, В.Б. (2010), Проектирование элементов машин (3-е изд.), Тата МакГроу-Хилл, стр. 441, ISBN 978-0-07-068179-8 .

[schnorr-4] Jump up to: ^а ^б ^с Справочник Шнорра , Шнорр, 2016 г., заархивировано из оригинала 3 октября 2016 г. , получено 4 октября 2016 г.

[5] Actionclear Современные винтовки

[6] Барретт, Ричард Т. (март 1990 г.). «Руководство по проектированию крепежа» (PDF) .

[formula1-7] Инфинити Ред Булл РБ10 Рено

[cirrus-8] Руководство по техническому обслуживанию самолетов Cirrus (PDF) , Cirrus Aircraft , 2014 г., стр. 32, 34, заархивировано из оригинала (PDF) 3 октября 2016 г. , получено 4 октября 2016 г.

[japan-9] Накамура, Такаши; Сузуки, Тецуо; Нобата, Арихиде (1998), Исследование характеристик реакции на землетрясение здания с изолированным основанием с использованием фрикционных демпферов с коническими дисковыми пружинами (PDF) , Материалы 10-го симпозиума по сейсмостойкой инженерии, стр. 2901–2906.

[Almen2-10] Алмен, Дж.О.; Ласло, А. (1936), Дисковая пружина однородного сечения , ASME 58, стр. 305–314.

[Curti-11] Курти, Грациано; Орландо, М. (1979), Новый расчет конических кольцевых дисковых пружин , Wire (28) 5, стр. 199–204.

[din92-12] DIN 2092: Тарельчатые пружины. Расчет , DIN, 2006 г.

[Ferrari-13] Феррари, Джаммарко (2013), «Новый метод расчета тарельчатых пружин с контактными плоскостями и уменьшенной толщиной» , Международный журнал производства, материалов и машиностроения , 3 (2), IJMMME 3 (2): 63–73, дои : 10.4018/ijmmme.2013040105

[14] «Продукты» . Архивировано из оригинала 21 июня 2020 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]