аксиома Паша

В геометрии в том виде , аксиома Паша — это утверждение плоской геометрии , неявно используемое Евклидом , которое не может быть выведено из постулатов в котором их дал Евклид. ^[1] Его существенная роль была открыта Морицем Пашем в 1882 году. ^[2]

Заявление

Две линии (черного цвета), пересекающие сторону треугольника. внутри страны и встречи с другими сторонами внутри и внешне

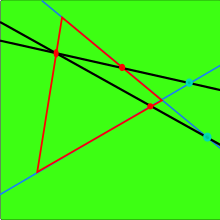
Аксиома гласит, что ^[3]

Аксиома Паша . Пусть A , B , C — три точки, которые не лежат на прямой , и пусть $a$ прямая в плоскости ABC , которая не пересекает ни одну из точек A , B , C. — Если прямая $a$ проходит через точку отрезка AB , она проходит также через точку отрезка AC или через точку отрезка BC .

Тот факт, что отрезки AC и BC не пересекаются прямой $a,$ доказывается в Приложении I,1, написанном П. Бернейсом . ^[4]

Более современная версия этой аксиомы выглядит следующим образом: ^[5]

Более современная версия аксиомы Паша : на плоскости, если линия пересекает одну сторону треугольника внутри , то она пересекает ровно одну другую сторону внутри и третью сторону снаружи , если она не проходит через вершину треугольника.

(В случае, если третья сторона параллельна нашей линии, мы считаем «пересечение на бесконечности» внешним.) Часто встречается более неформальная версия аксиомы:

Более неформальная версия аксиомы Паша : если линия, не проходящая через вершину треугольника, пересекает одну сторону треугольника, то она пересекает и другую сторону.

История

Паш опубликовал эту аксиому в 1882 году. ^[2] и показал, что аксиомы Евклида были неполными. Аксиома была частью подхода Паша к введению понятия порядка в плоскую геометрию.

Эквиваленты

В других трактовках элементарной геометрии, использующих различные наборы аксиом, аксиому Паша можно доказать как теорему; ^[6] это следствие аксиомы разделения плоскостей, если ее считать одной из аксиом. Гильберт использует аксиому Паша в своей аксиоматической трактовке евклидовой геометрии . ^[7] Учитывая остальные аксиомы системы Гильберта, можно показать, что аксиома Паша логически эквивалентна аксиоме разделения плоскостей. ^[8]

Использование Гильбертом аксиомы Паша

Дэвид Гильберт использует аксиому Паша в своей книге «Основы геометрии» , которая обеспечивает аксиоматическую основу евклидовой геометрии. В зависимости от издания он имеет номер II.4 или II.5. ^[7] Его заявление приведено выше.

В трактовке Гильберта эта аксиома появляется в разделе, посвященном аксиомам порядка, и называется плоской аксиомой порядка . Поскольку он не формулирует аксиому в терминах сторон треугольника (рассматриваемых как прямые, а не отрезки прямых), нет необходимости говорить о внутренних и внешних пересечениях прямой $а$ со сторонами треугольника ABC .

Предостережения

Аксиома Паша отличается от теоремы Паша , которая представляет собой утверждение о порядке четырех точек на прямой. Однако в литературе есть много случаев, когда аксиому Паша называют теоремой Паша. Ярким примером этого является Гринберг (1974 , стр. 67).

Аксиому Паша не следует путать с аксиомой Веблена-Янга для проективной геометрии . ^[9] что можно сформулировать как:

Аксиома Веблена-Янга для проективной геометрии : если прямая пересекает две стороны треугольника, то она пересекает и третью сторону.

нет упоминания о внутренних и внешних пересечениях В формулировке аксиомы Веблена-Янга, которая касается только свойства инцидентности пересечения прямых, . В проективной геометрии концепция «между» (требуемая для определения внутреннего и внешнего) недействительна, и все линии встречаются (поэтому проблема параллельных линий не возникает).

Примечания

^ Однако его можно вывести из более слабых аксиом разделения плоскостей, которые Евклид считал само собой разумеющимися, как показано в Памбучиане 2024.
^ Jump up to: ^а ^б Паш 1912 , с. 21
^ Гильберта Это взято из перевода Унгера 10-го издания «Основ геометрии» и имеет номер II.4.
^ Гильберт 1999 , с. 200, перевод Унгера.
^ Багспахер и Розенбаум 1998 , стр. 7
^ Уайли-младший, 1964 , с. 100
^ Jump up to: ^а ^б Гильберта аксиома II.5 в «Основах геометрии» (перевод Таунсенда указан ниже), в официальном английском переводе 10-го издания, переведенном Л. Унгером (также опубликованном Open Court), она имеет номер II.4. Между этими переводами есть несколько различий.
^ для этого нужны только аксиомы Гильберта I.1,2,3 и II.1,2,3. Доказательство дано у Фабера (1983 , стр. 116–117).
^ Багспахер и Розенбаум 1998 , стр. 6

Ссылки

Бойтельспехер, Альбрехт; Розенбаум, Юте (1998), Проективная геометрия: от основ к приложениям , Cambridge University Press , ISBN 978-0-521-48364-3 , МР 1629468
Фабер, Ричард Л. (1983), Основы евклидовой и неевклидовой геометрии , Нью-Йорк: Marcel Dekker, Inc., ISBN 978-0-8247-1748-3
Гринберг, Марвин Джей (1974), Евклидова и неевклидова геометрия: развитие и история (1-е изд.), Сан-Франциско: WH Freeman, ISBN 978-0-7167-0454-6
- Гринберг, Марвин Джей (2007), Евклидова и неевклидова геометрия: развитие и история (4-е изд.), Сан-Франциско: WH Freeman, ISBN 978-0-7167-9948-1
Гильберт, Давид (1903), Основы геометрии (на немецком языке), Лейпциг: Б. Г. Тойбнер
- Гильберт, Дэвид (1950) [1902], Основы геометрии (PDF) , перевод Таунсенда, Э.Дж., ЛаСалль, Иллинойс: Open Court Publishing
- Гильберт, Дэвид (1999) [1971], Основы геометрии , перевод Унгера, Лео (2-е изд.), LaSalle, IL: Open Court Publishing, ISBN 978-0-87548-164-7
Мойс, Эдвин (1990), Элементарная геометрия с продвинутой точки зрения (Третье изд.), Аддисон-Уэсли, Ридинг, Массачусетс, стр. 74, ISBN 978-0-201-50867-3
Памбучян, Виктор (2011), «Аксиоматика упорядоченной геометрии: I. Упорядоченные пространства инцидентности», Expositiones Mathematicae (29): 24–66, doi : 10.1016/j.exmath.2010.09.004
Памбучиан, Виктор (2024), «Почему Евклиду не понадобилась аксиома Паша?», Journal of Geometry (115), doi : 10.1007/s00022-024-00712-x
Паш, Мориц (1912) [первое издание 1882 г.], лекции по современной геометрии (на немецком языке) (2-е изд.), Лейпциг: Б. Г. Тойбнер
Уайли-младший, Кларенс Рэймонд (1964), Основы геометрии , Нью-Йорк: McGraw-Hill, ISBN 978-0-070-72191-3
- Уайли-младший, CR (2009) [1964], Основы геометрии , Минеола, Нью-Йорк: Dover Publications, ISBN 978-0-486-47214-0

Внешние ссылки

Вайсштейн, Эрик В. «Аксиома Паша» . Математический мир .

[1] Однако его можно вывести из более слабых аксиом разделения плоскостей, которые Евклид считал само собой разумеющимися, как показано в Памбучиане 2024.

[Pasch-2] Jump up to: ^а ^б Паш 1912 , с. 21

[3] Гильберта Это взято из перевода Унгера 10-го издания «Основ геометрии» и имеет номер II.4.

[4] Гильберт 1999 , с. 200, перевод Унгера.

[5] Багспахер и Розенбаум 1998 , стр. 7

[6] Уайли-младший, 1964 , с. 100

[Hilbert-7] Jump up to: ^а ^б Гильберта аксиома II.5 в «Основах геометрии» (перевод Таунсенда указан ниже), в официальном английском переводе 10-го издания, переведенном Л. Унгером (также опубликованном Open Court), она имеет номер II.4. Между этими переводами есть несколько различий.

[8] для этого нужны только аксиомы Гильберта I.1,2,3 и II.1,2,3. Доказательство дано у Фабера (1983 , стр. 116–117).

[9] Багспахер и Розенбаум 1998 , стр. 6

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]