Правило Литтлвуда-Ричардсона

В математике правило Литтлвуда -Ричардсона представляет собой комбинаторное описание коэффициентов, возникающих при разложении произведения двух функций Шура в линейную комбинацию других функций Шура. Эти коэффициенты представляют собой натуральные числа, которые правило Литтлвуда-Ричардсона описывает как подсчет определенных асимметричных таблиц . Они встречаются во многих других математических контекстах, например, как кратность при разложении тензорных произведений , конечномерных представлений общих линейных групп или при разложении некоторых индуцированных представлений в теории представлений симметрической группы , или в области алгебраическая комбинаторика, имеющая дело с таблицами Юнга и симметричными полиномами .

Коэффициенты Литтлвуда – Ричардсона зависят от трех разделов , скажем $\lambda ,\mu ,\nu$ , из них $\lambda$ и $\mu$ описать умножаемые функции Шура и $\nu$ дает функцию Шура, коэффициентом которой является эта линейная комбинация; другими словами, это коэффициенты $c_{\lambda ,\mu }^{\nu }$ такой, что

s_{\lambda }s_{\mu }=\sum _{\nu }c_{\lambda ,\mu }^{\nu }s_{\nu }.

Правило Литтлвуда-Ричардсона гласит, что $c_{\lambda ,\mu }^{\nu }$ равно количеству таблиц Литтлвуда – Ричардсона косой формы. $\nu /\lambda$ и веса $\mu$ .

История

К сожалению, правило Литтлвуда-Ричардсона доказать гораздо труднее, чем предполагалось на первый взгляд. Автору однажды сказали, что правило Литтлвуда-Ричардсона помогло людям попасть на Луну, но не было доказано до тех пор, пока они туда не прибыли.

Гордон Джеймс ( 1987 )

Правило Литтлвуда-Ричардсона было впервые сформулировано Д.Э. Литтлвудом и А.Р. Ричардсоном ( 1934 , теорема III, стр. 119), но, хотя они и провозгласили его теоремой, они доказали его только в некоторых довольно простых частных случаях. Робинсон ( 1938 ) утверждал, что завершил свое доказательство, но в его аргументации были пробелы, хотя они были настолько неясно написаны, что эти пробелы некоторое время не замечались, и его аргументация воспроизведена в книге ( Литтлвуд 1950 ). Некоторые пробелы позже были заполнены Макдональдом (1995) . Первые строгие доказательства этого правила были даны через четыре десятилетия после его открытия Шютценбергером ( 1977 ) и Томасом (1974) , после того как необходимая комбинаторная теория была разработана К. Шенстедом ( 1961 ), Шютценбергером ( 1963 ) и Кнутом (1963 ). 1970 ) в своей работе над перепиской Робинсона-Шенстеда . Сейчас существует несколько коротких доказательств этого правила, например ( Гашаров 1998 ) и ( Стембридж 2002 ) с использованием инволюций Бендера-Кнута . Литтельманн (1994) использовал модель пути Литтельмана для обобщения правила Литтлвуда-Ричардсона на другие полупростые группы Ли.

Правило Литтлвуда-Ричардсона печально известно количеством ошибок, которые появились до его полного опубликованного доказательства. Несколько опубликованных попыток доказать его неполны, и особенно трудно избежать ошибок при ручных вычислениях с его помощью: даже оригинальный пример Д.Э. Литтлвуда и А.Р. Ричардсона ( 1934 ) содержит ошибку.

Таблицы Литтлвуда – Ричардсона

Таблица Литтлвуда-Ричардсона представляет собой косую полустандартную таблицу с дополнительным свойством, заключающимся в том, что последовательность, полученная путем объединения ее перевернутых строк, представляет собой решеточное слово (или решетчатую перестановку), что означает, что в каждой начальной части последовательности любое число $i$ встречается по крайней мере так же часто, как число $i+1$ . Другая эквивалентная (хотя и не совсем очевидная) характеристика состоит в том, что сама таблица и любая таблица, полученная из нее путем удаления некоторого количества ее крайних левых столбцов, имеют слабо убывающий вес. Было обнаружено множество других комбинаторных понятий, которые оказались в биекции с таблицами Литтлвуда-Ричардсона и, следовательно, также могут быть использованы для определения коэффициентов Литтлвуда-Ричардсона.

Пример

Рассмотрим случай, когда $\lambda =(2,1)$ , $\mu =(3,2,1)$ и $\nu =(4,3,2)$ . Тогда тот факт, что $c_{\lambda ,\mu }^{\nu }=2$ можно сделать вывод из того факта, что две таблицы, показанные справа, являются единственными двумя таблицами Литтлвуда – Ричардсона формы. $\nu /\lambda$ и вес $\mu$ . Действительно, поскольку последний квадрат в первой непустой строке диаграммы перекоса может содержать только запись 1, вся первая строка должна быть заполнена элементами 1 (это верно для любой таблицы Литтлвуда – Ричардсона); в последнем поле второй строки мы можем поместить только 2 из-за строгости столбца и того факта, что наше слово решетки не может содержать более крупную запись, пока оно не содержит 2. Для первого поля второй строки мы теперь можем либо использовать 1 или 2. Как только эта запись выбрана, третья строка должна содержать оставшиеся записи, чтобы составить вес (3,2,1), в слабо возрастающем порядке, поэтому у нас больше не остается выбора; в обоих случаях оказывается, что мы находим таблицу Литтлвуда–Ричардсона.

Более геометрическое описание

Условие, согласно которому последовательность записей, считываемых из таблицы в несколько своеобразном порядке, образует решетчатое слово, можно заменить более локальным и геометрическим условием. Поскольку в полустандартной таблице одинаковые записи никогда не встречаются в одном и том же столбце, можно нумеровать копии любого значения справа налево, что соответствует их порядку появления в последовательности, которая должна быть словом решетки. Назовите номер, связанный таким образом с каждой записью, ее индексом и запишите запись i с индексом j как i [ j ]. Теперь, если некоторая таблица Литтлвуда–Ричардсона содержит запись $i>1$ с индексом j , то эта запись i [ j ] должна находиться в строке строго ниже записи $(i-1)[j]$ (что, безусловно, тоже имеет место, поскольку запись i − 1 встречается не реже, чем запись i ). Фактически запись i [ j ] также должна встречаться в столбце не дальше вправо, чем та же самая запись. $(i-1)[j]$ (что на первый взгляд кажется более строгим условием). Если вес таблицы Литтлвуда-Ричардсона фиксирован заранее, то можно сформировать фиксированный набор индексированных записей, и если они размещены таким образом, чтобы соблюдать эти геометрические ограничения, в дополнение к ограничениям полустандартных таблиц и условию, что индексированные копии одних и тех же записей должны соблюдать порядок индексов справа налево, тогда результирующие таблицы гарантированно будут таблицами Литтлвуда – Ричардсона.

Алгоритмическая форма правила

Как указано выше, таблица Литтлвуда-Ричардсона дает комбинаторное выражение для отдельных коэффициентов Литтлвуда-Ричардсона, но не указывает на практический метод перечисления таблиц Литтлвуда-Ричардсона для нахождения значений этих коэффициентов. Действительно, для данного $\lambda ,\mu ,\nu$ не существует простого критерия, позволяющего определить, имеют ли какие-либо таблицы Литтлвуда–Ричардсона форму $\nu /\lambda$ и веса $\mu$ существуют вообще (хотя есть ряд необходимых условий, самое простое из которых — $|\lambda |+|\mu |=|\nu |$ ); поэтому кажется неизбежным, что в некоторых случаях приходится проводить тщательный поиск только для того, чтобы обнаружить, что решений не существует.

Тем не менее, правило приводит к весьма эффективной процедуре определения полного разложения произведения функций Шура, другими словами, для определения всех коэффициентов $c_{\lambda ,\mu }^{\nu }$ для фиксированных λ и µ, но варьирующихся ν. Это фиксирует вес создаваемых таблиц Литтлвуда-Ричардсона и «внутреннюю часть» λ их формы, но оставляет «внешнюю часть» ν свободной. Поскольку вес известен, набор индексированных записей в геометрическом описании фиксирован. Теперь для последовательных индексированных записей можно попробовать все возможные позиции, разрешенные геометрическими ограничениями, при поиске с возвратом . Записи можно пробовать в порядке возрастания, а среди равных записей их можно пробовать по убыванию индекса. Последний момент является ключом к эффективности процедуры поиска: тогда запись i [ j ] ограничивается размещением в столбце справа от $i[j+1]$ , но не дальше вправо, чем $i-1[j]$ (если такие записи присутствуют). Это сильно ограничивает набор возможных позиций, но всегда оставляет хотя бы одну допустимую позицию для $i[j]$ ; таким образом, каждое размещение записи приведет к появлению по крайней мере одной полной таблицы Литтлвуда – Ричардсона, и дерево поиска не содержит тупиков.

Аналогичный метод можно использовать для нахождения всех коэффициентов $c_{\lambda ,\mu }^{\nu }$ для фиксированных λ и ν, но изменяющихся µ.

Коэффициенты Литтлвуда – Ричардсона

Коэффициенты Литтлвуда–Ричардсона c ^н
_λμ появляются следующими взаимосвязанными способами:

Это структурные константы произведения в кольце симметричных функций относительно базиса функций Шура.

s_{\lambda }s_{\mu }=\sum c_{\lambda \mu }^{\nu }s_{\nu }

или, что эквивалентно, c ^н
_λμ — скалярное произведение s _ν и s _λ s _μ .

Они выражают косые функции Шура через функции Шура.

s_{\nu /\lambda }=\sum _{\mu }c_{\lambda \mu }^{\nu }s_{\mu }.

с ^н
_λμ появляются как числа пересечений грассманиана :

\sigma _{\lambda }\sigma _{\mu }=\sum c_{\lambda \mu }^{\nu }\sigma _{\nu }

где σ _µ — класс многообразия Шуберта грассманиана, соответствующего µ .

с ^н
_λµ — количество раз неприводимого представления V _λ ⊗ V _µ произведения симметрических групп S _{| λ |} × С _{| | |} появляется в ограничении представления V _ν группы S _{| ν |} в С _{| λ |} × С _{| | |} . По взаимности Фробениуса это также количество раз, когда V _ν встречается в представлении S _{| ν |} индуцированный из V _λ ⊗ V _µ .
с ^н
_λμ появляются при разложении тензорного произведения ( Фултон 1997 ) двух модулей Шура (неприводимых представлений специальных линейных групп)

E^{\lambda }\otimes E^{\mu }=\bigoplus _{\nu }(E^{\nu })^{\oplus c_{\lambda \mu }^{\nu }}.

с ^н
_λμ — это количество стандартных таблиц Юнга формы ν / μ, которые эквивалентны некоторой фиксированной стандартной таблице Юнга формы λ .
с ^н
_λμ — количество таблиц Литтлвуда–Ричардсона формы ν / λ и веса μ .
с ^н
_λμ — количество изображений между µ и ν/λ.

Особые случаи

Формула Пьери

Формула Пьери , представляющая собой частный случай правила Литтлвуда–Ричардсона в случае, когда одно из разбиений имеет только одну часть , утверждает, что

S_{\mu }S_{n}=\sum _{\lambda }S_{\lambda }

где S _n — функция Шура разбиения с одной строкой, а сумма рассчитана по всем разбиениям λ, полученным из µ добавлением n элементов к диаграмме Феррера , а не двух в одном столбце.

Прямоугольные перегородки

Если оба раздела имеют прямоугольную форму, сумма также не содержит кратности ( Okada 1998 ). Зафиксируйте a , b , p и q положительные целые числа с p $\geq$ q . Обозначим через $(a^{p})$ раздел с p частями длины a . Разделы, индексирующие нетривиальные компоненты $s_{(a^{p})}s_{(b^{q})}$ это эти перегородки $\lambda$ с длиной $\leq p+q$ такой, что

$\lambda _{q+1}=\lambda _{q+2}=\cdots =\lambda _{p}=a,$
$\lambda _{q}\geq \mathrm {max} (a,b)$
$\lambda _{i}+\lambda _{p+q-i+1}=a+b,\quad {i=1,\dots ,q}.$

Например,

.

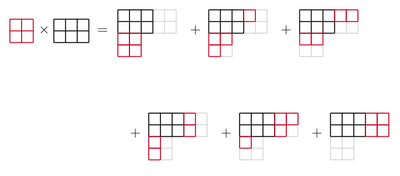
Обобщения

Приведенные коэффициенты Кронекера симметричной группы

Приведенный коэффициент Кронекера симметричной группы ${\bar {C}}_{\lambda ,\mu ,\nu }$ представляет собой обобщение $c_{\lambda ,\mu }^{\nu }$ трем произвольным диаграммам Юнга $\lambda ,\mu ,\nu$ , который симметричен относительно перестановок трех диаграмм.

Раскосные функции Шура

Зелевинский (1981) расширил правило Литтлвуда-Ричардсона, чтобы исказить функции Шура следующим образом:

s_{\lambda }s_{\mu /\nu }=\sum _{\lambda +\omega (T_{\geq j})\in P}s_{\lambda +\omega (T)}

где сумма ведется по всем таблицам T на µ/ν таким, что для всех j последовательность целых чисел λ+ω( T _{≥ j} ) не возрастает, а ω — вес.

Числа Ньюэлла-Литтлвуда

Числа Ньюэлла-Литтлвуда определяются из коэффициентов Литтлвуда-Ричардсона кубическим выражением ^[1]

N_{\mu ,\nu ,\lambda }=\sum _{\alpha ,\beta ,\gamma }c_{\alpha ,\beta }^{\mu }c_{\alpha ,\gamma }^{\nu }c_{\beta ,\gamma }^{\lambda }

Числа Ньюэлла-Литтлвуда дают некоторые кратности тензорного произведения конечномерных представлений классических групп Ли типов $B,C,D$ .

Условие неисчезновения размеров диаграммы Юнга $c_{\lambda ,\mu }^{\nu }\neq 0\implies |\lambda |+|\mu |=|\nu |$ приводит к

N_{\mu ,\nu ,\lambda }\neq 0\implies \left\{{\begin{array}{l}||\lambda |-|\mu ||\leq |\nu |\leq |\lambda |+|\mu |\\|\lambda |+|\mu |+|\nu |\in 2\mathbb {Z} \end{array}}\right.

Числа Ньюэлла-Литтлвуда являются обобщением коэффициентов Литтлвуда-Ричардсона в том смысле, что

|\mu |+|\nu |=|\lambda |\implies N_{\mu ,\nu ,\lambda }=c_{\mu ,\nu }^{\lambda }

Числа Ньюэлла-Литтлвуда, включающие диаграмму Юнга только с одной строкой, подчиняются правилу типа Пьери: $N_{(k),\mu ,\nu }$ это количество способов удалить ${\frac {k+|\mu |-|\nu |}{2}}$ коробки из $\mu$ (из разных столбцов), затем добавьте ${\frac {k-|\mu |+|\nu |}{2}}$ коробки (в разные столбцы), чтобы сделать $\nu$ . ^[1]

Числа Ньюэлла-Литтлвуда — это структурные константы ассоциативной и коммутативной алгебры, базисными элементами которой являются разбиения с произведением $\mu \times \nu =\sum _{\lambda }N_{\mu ,\nu ,\lambda }\lambda$ . Например,

(1)\times (k)=(k-1)+(k+1)+(k,1)\quad {\text{(Newell–Littlewood)}}

(1)\times (k)=(k+1)+(k,1)\quad {\text{(Littlewood–Richardson)}}

Примеры

Приведенные ниже примеры коэффициентов Литтлвуда – Ричардсона даны в терминах произведений полиномов Шура S _π , индексированных разбиениями π, с использованием формулы

S_{\lambda }S_{\mu }=\sum c_{\lambda \mu }^{\nu }S_{\nu }.

Все коэффициенты с $|\nu |$ не более 4 даны:

S ₀ S _π = S _π для любого π. где S ₀ =1 — полином Шура пустого разбиения
С ₁ С ₁ = С ₂ + С ₁₁
С ₂ С ₁ = С ₃ + С ₂₁
С ₁₁ С ₁ = С ₁₁₁ + С ₂₁
С ₃ С ₁ = С ₄ + С ₃₁
С ₂₁ С ₁ = С ₃₁ + С ₂₂ + С ₂₁₁
С ₂ С ₂ = С ₄ + С ₃₁ + С ₂₂
С ₂ С ₁₁ = С ₃₁ + С ₂₁₁
С ₁₁₁ С ₁ = С ₁₁₁₁ + С ₂₁₁
С ₁₁ С ₁₁ = С ₁₁₁₁ + С ₂₁₁ + С ₂₂

коэффициентов для небольших разделов равны 0 или 1, что происходит, в частности, когда один из факторов имеет форму Sn _{Большинство} или S _11...1 из-за формулы Пьери и ее транспонированного аналога. Самый простой пример с коэффициентом больше 1 имеет место, когда ни один из факторов не имеет такого вида:

S ₂₁ S ₂₁ = S ₄₂ + S ₄₁₁ + S ₃₃ + 2 S ₃₂₁ + S ₃₁₁₁ + S ₂₂₂ + S ₂₂₁₁ .

Для больших разделов коэффициенты становятся более сложными. Например,

S ₃₂₁ S ₃₂₁ = S ₆₄₂ + S ₆₄₁₁ + S ₆₃₃ +2 S ₆₃₂₁ + S ₆₃₁₁₁ + S ₆₂₂₂ + S ₆₂₂₁₁ + S ₅₅₂ + S ₅₅₁₁ +2 S ₅₄₃ +4 S ₅₄₂₁ +2 S ₅₄₁₁₁ +3 S ₅₃₃₁ +3 S ₅₃₂₂ +4 S ₅₃₂₁₁ + S ₅₃₁₁₁₁ +2 S ₅₂₂₂₁ + S ₅₂₂₁₁₁ + S ₄₄₄ +3 S ₄₄₃₁ +2 S ₄₄₂₂ +3 S ₄₄₂₁₁ + S ₄₄₁₁₁₁ +3 S ₄₃₃₂ +3 S ₄₃₃₁₁ +4 S ₄₃₂₂₁ +2 S ₄₃₂₁₁₁ + S ₄₂₂₂₂ + S ₄₂₂₂₁₁ + S ₃₃₃₃ +2 S ₃₃₃₂₁ + S ₃₃₃₁₁₁ + S ₃₃₂₂₂ + S ₃₃₂₂₁₁ с 34 членами и общей кратностью 62, а наибольший коэффициент равен 4
S ₄₃₂₁ S ₄₃₂₁ представляет собой сумму 206 слагаемых с общей кратностью 930, а наибольший коэффициент равен 18.
S ₅₄₃₂₁ S ₅₄₃₂₁ представляет собой сумму 1433 слагаемых с общей кратностью 26704, а наибольший коэффициент (у S _86543211 ) равен 176.
S ₆₅₄₃₂₁ S ₆₅₄₃₂₁ представляет собой сумму 10873 слагаемых с общей кратностью 1458444 (поэтому среднее значение коэффициентов больше 100, а их число может достигать 2064).

Первоначальный пример, приведенный Литтлвудом и Ричардсоном (1934 , стр. 122–124), был следующим (после поправки на 3 таблицы, которые они нашли, но забыли включить в окончательную сумму):

S ₄₃₁ S ₂₂₁ = S ₆₅₂ + S ₆₅₁₁ + S ₆₄₃ 2 S ₆₄₂₁ + S ₆₄₁₁₁ + S ₆₃₃₁ + S ₆₃₂₂ + + S ₆₃₂₁₁ + S ₅₅₃ + 2 S ₅₅₂₁ + S ₅₅₁₁₁ + 2 S ₅₄₃₁ + 2 S ₅₄₂₂ + 3 S ₅₄₂₁₁ + S ₅₄₁₁₁₁ + S ₅₃₃₂ + S ₅₃₃₁₁ 2 S ₅₃₂₂₁ + S ₅₃₂₁₁₁ + S ₄₃₃₂₁ + + S ₄₄₃₂ + 2 S ₄₄₂₂₁ + S ₄₄₂₁₁₁ + S ₄₃₂₂₂ + S ₄₄₃₁₁ + S ₄₃₂₂₁₁

с 26 терминами из следующих 34 таблиц:

....11 ....11 ....11 ....11 ....11 ....11 ....11 ....11 ....11    
...22  ...22  ...2   ...2   ...2   ...2   ...    ...    ...
.3     .      .23    .2     .3     .      .22    .2     .2     
       3             3      2      2      3      23     2      
                                   3                    3

....1  ....1  ....1  ....1  ....1  ....1  ....1  ....1  ....1   
...12  ...12  ...12  ...12  ...2   ...1   ...1   ...2   ...1
.23    .2     .3     .      .13    .22    .2     .1     .2      
       3      2      2      2      3      23     23     2
                     3                                  3

....1  ....1  ....1  ....1  ....1  ....1  ....1  ....1   
...2   ...2   ...2   ...    ...    ...    ...    ...    
.1     .3     .      .12    .12    .1     .2     .2      
2      1      1      23     2      22     13     1
3      2      2             3      3      2      2
              3                                  3

....   ....   ....   ....   ....   ....   ....   ....   
...1   ...1   ...1   ...1   ...1   ...    ...    ...    
.12    .12    .1     .2     .2     .11    .1     .1      
23     2      22     13     1      22     12     12
       3      3      2      2      3      23     2
                            3                    3

Вычисление косых функций Шура аналогично. Например, 15 таблиц Литтлвуда – Ричардсона для ν = 5432 и λ = 331 имеют вид

...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11
...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2
.11   .11   .11   .12   .11   .12   .13   .13   .23   .13   .13   .12   .12   .23   .23
12    13    22    12    23    13    12    24    14    14    22    23    33    13    34

поэтому S _5432/331 = Σ c ^н
_λμ S _μ = S ₅₂ + S ₅₁₁ + S ₄₁₁₁ + S ₂₂₂₁ + 2 S ₄₃ + 2 S ₃₂₁₁ + 2 S ₃₂₂ + 2 S ₃₃₁ + 3 S ₄₂₁ ( Фултон 1997 , стр. 64).

Примечания

^ Jump up to: ^а ^б Гао, Шилян; Ореловиц, Гидон; Йонг, Александр (2021). «Числа Ньюэлла-Литтлвуда». Пер. амер. Математика. Соц . 374 (9): 6331–6366. arXiv : 2005.09012v1 . дои : 10.1090/tran/8375 . S2CID 218684561 .

Ссылки

Фултон, Уильям (1997), Таблицы Янга , Студенческие тексты Лондонского математического общества, том. 35, Издательство Кембриджского университета , с. 121, ISBN 978-0-521-56144-0 , МР 1464693
Гашаров, Весселин (1998), «Краткое доказательство правила Литтлвуда-Ричардсона» , European Journal of Combinatorics , 19 (4): 451–453, doi : 10.1006/eujc.1998.0212 , ISSN 0195-6698 , MR 1630540
Джеймс, Гордон (1987), «Теория представлений симметричных групп», Аркатская конференция по представлениям конечных групп (Арката, Калифорния, 1986) , Proc. Симпозиумы. Чистая математика., вып. 47, Провиденс, Род-Айленд: Американское математическое общество , стр. 111–126, MR 0933355.
Кнут, Дональд Э. (1970), «Перестановки, матрицы и обобщенные таблицы Юнга» , Pacific Journal of Mathematics , 34 (3): 709–727, doi : 10.2140/pjm.1970.34.709 , ISSN 0030-8730 , MR 0272654
Литтельманн, Питер (1994), «Правило Литтлвуда-Ричардсона для симметризуемых алгебр Каца-Муди» (PDF) , Invent. Математика. , 116 : 329–346, Бибкод : 1994InMat.116..329L , doi : 10.1007/BF01231564 , S2CID 85546837
Литтлвуд, Дадли Э. (1950), Теория групповых характеров и матричные представления групп , AMS Chelsea Publishing, Провиденс, Род-Айленд, ISBN 978-0-8218-4067-2 , МР 0002127
Литтлвуд, Делавэр; Ричардсон, А.Р. (1934), «Групповые персонажи и алгебра», «Философские труды Лондонского королевского общества». Серия A, содержащая статьи математического или физического характера , 233 (721–730), Королевское общество: 99–141, Bibcode : 1934RSPTA.233...99L , doi : 10.1098/rsta.1934.0015 , ISSN 0264-3952 , JSTOR 91293
Макдональд, И.Г. (1995), Симметричные функции и полиномы Холла , Оксфордские математические монографии (2-е изд.), The Clarendon Press Oxford University Press, ISBN 978-0-19-853489-1 , MR 1354144 , заархивировано из оригинала 11 декабря 2012 г.
Окада, Соичи (1998), «Применение второстепенных формул суммирования к прямоугольным представлениям классических групп», Journal of Algebra , 205 (2): 337–367, doi : 10.1006/jabr.1997.7408 , ISSN 0021-8693 , MR 1632816
Робинсон, Г. де Б. (1938), «О представлениях симметричной группы», Американский журнал математики , 60 (3), The Johns Hopkins University Press: 745–760, doi : 10.2307/2371609 , ISSN 0002- 9327 , JSTOR 2371609 Збл 0019.25102
Шенстед, К. (1961), «Самые длинные возрастающие и убывающие подпоследовательности» , Canadian Journal of Mathematics , 13 : 179–191, doi : 10.4153/CJM-1961-015-3 , ISSN 0008-414X , MR 0121305
Шютценбергер, член парламента (1963), «Quelques remarques sur une Construction de Schensted», Mathematica Scandinavica , 12 : 117–128, doi : 10.7146/math.scand.a-10676 , ISSN 0025-5521 , MR 0190017
Шютценбергер, Марсель-Поль (1977), «Соответствие Робинсона» , Комбинаторика и представление симметричной группы (Actes Table Ronde CNRS, Univ. Louis-Pasteur Strasbourg, Страсбург, 1976) , Конспекты лекций по математике, том. 579, Берлин, Нью-Йорк: Springer-Verlag , стр. 59–113 , номер домена : 10.1007/BFb0090012 , ISBN. 978-3-540-08143-2 , МР 0498826
Стембридж, Джон Р. (2002), «Краткое доказательство правила Литтлвуда-Ричардсона» (PDF) , Electronic Journal of Combinatorics , 9 (1): Примечание 5, 4 стр. (электронный), doi : 10.37236/1666 , ISSN 1077-8926 , МР 1912814
Томас, Гланфрвд П. (1974), Алгебры Бакстера и функции Шура , доктор философии. Диссертация, Суонси: Университетский колледж Суонси
ван Леувен, Марк А.А. (2001), «Правило Литтлвуда-Ричардсона и связанная с ним комбинаторика» (PDF) , Взаимодействие комбинаторики и теории представлений , MSJ Mem., vol. 11, Токио: Матем. Соц. Япония, стр. 95–145, MR 1862150.
Зелевинский, А.В. (1981), «Обобщение правила Литтлвуда-Ричардсона и соответствия Робинсона-Шенстеда-Кнута», Journal of Algebra , 69 (1): 82–94, doi : 10.1016/0021-8693(81)90128 -9 , ISSN 0021-8693 , МР 0613858

Внешние ссылки

Онлайн-программа , разлагающая произведения функций Шура по правилу Литтлвуда – Ричардсона.

[gao20-1] Jump up to: ^а ^б Гао, Шилян; Ореловиц, Гидон; Йонг, Александр (2021). «Числа Ньюэлла-Литтлвуда». Пер. амер. Математика. Соц . 374 (9): 6331–6366. arXiv : 2005.09012v1 . дои : 10.1090/tran/8375 . S2CID 218684561 .

[1]