Атака с компромиссом между временем/памятью/данными

Атака компромисса времени/памяти/данных — это тип криптографической атаки , при которой злоумышленник пытается добиться ситуации, аналогичной компромиссу пространства-времени , но с дополнительным параметром data , представляющим объем данных, доступных злоумышленнику. Злоумышленник уравновешивает или уменьшает один или два из этих параметров в пользу другого или двух. Этот тип атаки очень сложен, поэтому большинство используемых шифров и схем шифрования не предназначены для противодействия ему.

История

Атаки компромисса на симметричные криптосистемы начались в 1980 году, когда Мартин Хеллман предложил метод компромисса между временем и памятью для взлома блочных шифров с помощью $N$ возможные ключи во времени $T$ и память $M$ связаны кривой компромисса $T{M^{2}}={N^{2}}$ где $1\leq T\leq N$. Позже, в 1995 году, Бэббидж и Голич разработали другую компромиссную атаку для потоковых шифров с новой границей, такой, что $TM=N$ для $1\leq T\leq D$ где $D$ — выходные данные, доступные криптоаналитику в режиме реального времени.

Механика атаки

Эта атака представляет собой специальную версию общей криптоаналитической атаки на компромисс между временем и памятью, которая состоит из двух основных фаз:

1. Предварительная обработка:
   На этом этапе злоумышленник исследует структуру криптосистемы и может записать свои выводы в большие таблицы. Это может занять много времени.
2. В реальном времени:
   На этом этапе криптоаналитику предоставляются реальные данные, полученные из определенного неизвестного ключа. Затем они пытаются использовать эти данные с предварительно вычисленной таблицей на этапе предварительной обработки , чтобы найти конкретный ключ за как можно меньшее время.

Любая атака с компромиссом между временем/памятью/данными имеет следующие параметры:

$N$ размер пространства поиска

$P$ время, необходимое для предварительной обработки этапа

$T$ время, необходимое для реального времени фазы

$M$ объем памяти, доступный злоумышленнику

$D$ объем данных в реальном времени, доступных злоумышленнику

Хеллмана на

Для блочных шифров пусть $N$ — общее количество возможных ключей, а также предположим, что количество возможных открытых текстов и зашифрованных текстов должно быть $N$. Также пусть данные будут одним блоком зашифрованного текста определенного аналога открытого текста. Если рассмотреть отображение из ключа $x$ к зашифрованному тексту $y$ как функция случайной перестановки $f$ над $N$ точечное пространство, и если эта функция $f$ является обратимым; нам нужно найти обратную функцию ${f}^{-1}(y)=x$.Метод Хеллмана для инвертирования этой функции:

На этапе предварительной обработки

Постарайтесь прикрыть $N$ точечное пространство с помощью $m\times t$ прямоугольная матрица, построенная путем итерации функции $f$ на $m$ случайные отправные точки в $N$ для $t$ раз. Начальные точки — это самый левый столбец матрицы, а конечные точки — самый правый столбец. Затем сохраните пары начальной и конечной точек в порядке возрастания значений конечных точек.

Hellman's Matrix

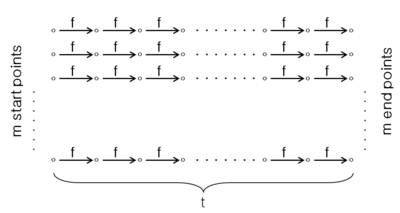
Теперь одна матрица не сможет охватить всю $N$ космос. Но если мы добавим в матрицу больше строк, мы получим огромную матрицу, включающую восстановленные точки более одного раза. Итак, находим критическое значение $m$ при котором матрица содержит ровно $m$ разные точки. Рассмотрим первый $m$ пути от начальных точек до конечных точек не пересекаются с $mt$ точек, так что следующий путь, имеющий хотя бы одну общую точку с одним из этих предыдущих путей и включающий в себя ровно $t$ точки. Эти два набора $mt$ и $t$ точки не пересекаются из-за парадокса дня рождения, если мы убедимся, что $t\cdot mt\leq N$. Мы достигаем этого, применяя правило остановки матрицы : $m{t}^{2}=N$.

Тем не менее, $m\times t$ матрица с $m{t}^{2}=N$ покрывает часть $mt/N=1/t$ всего пространства. Чтобы создать $t$ чтобы охватить все пространство, мы используем вариант $f$ определенный: ${f}_{i}(x)={h}_{i}(f(x))$ и ${h}_{i}$ это простая манипуляция, такая как изменение порядка битов $f(x)$ (более подробную информацию можно найти в оригинальной статье). И можно видеть, что общее время предварительной обработки равно $P\approx N$. Также $M=mt$ поскольку нам нужно хранить только пары начальной и конечной точек, и у нас есть $t$ матрицы каждая из $m$ пары.

На этапе реального времени

Общий объем вычислений, необходимый для нахождения $f^{-1}(y)$ является $T=t^{2}$ потому что нам нужно сделать $t$ попыток инверсии, так как она, скорее всего, будет покрыта одной матрицей, и каждая из попыток занимает $t$ оценки некоторых $f_{i}$. Оптимальная кривая компромисса получается с помощью правила остановки матрицы $m{t}^{2}=N$ и мы получаем $T{M^{2}}={N^{2}},P=N,D=1$ и выбор $T$ и $M$ зависит от стоимости каждого ресурса.

По словам Хеллмана, если имеющийся блочный шифр обладает свойством, заключающимся в том, что отображение его ключа в зашифрованный текст является функцией случайной перестановки. $f$ над $N$ точечное пространство, и если это $f$ обратима, то компромиссные отношения становятся намного лучше: $TM=N$.

Бэббиджа и Голика на

Для потоковых шифров $N$ определяется количеством внутренних состояний битового генератора, вероятно, отличным от количества ключей. $D$ — это количество первых псевдослучайных битов, созданных генератором. Наконец, цель злоумышленника — найти одно из фактических внутренних состояний генератора битов, чтобы с этого момента он мог запустить генератор для генерации остальной части ключа. Свяжите каждый из возможных $N$ внутренние состояния битового генератора с соответствующей строкой, состоящей из первых $log(N)$ биты, полученные при запуске генератора из этого состояния путем отображения $f(x)=y$ из штатов $x$ для вывода префиксов $y$. Это предыдущее отображение считается случайной функцией над $N$ точки общего пространства. Чтобы инвертировать эту функцию, злоумышленник устанавливает следующее.

1. На этапе предварительной обработки выберите $M$ случайный ${x}_{i}$ состояния и вычислить соответствующие им ${y}_{i}$ выходные префиксы.
2. Храните пары $({x}_{i},{y}_{i})$ в порядке возрастания ${y}_{i}$ в большом столе.
3. На этапе реального времени у вас есть $D+log(N)-1$ сгенерированные биты. Посчитайте из них всех $D$ возможные комбинации ${y}_{1},{y}_{2},...,{y}_{D},$ последовательных битов длиной $log(N)$.
4. Ищите каждый ${y}_{i}$ в сгенерированной таблице, что занимает время регистрации.
5. Если у вас есть хит, это ${y}_{i}$ соответствует внутреннему состоянию ${x}_{i}$ битового генератора, из которого можно запустить генератор для получения остальной части ключа.
6. Парадокс дня рождения гарантирует, что два подмножества пространства с $N$ точки имеют пересечение, если произведение их размеров больше $N$.

Этот результат атаки Birthday дает условие $DM=N$ со временем атаки $T=D$ и время предварительной обработки $P=M$ это всего лишь конкретная точка на кривой компромисса $TM=N$. Мы можем обобщить это соотношение, если проигнорируем некоторые доступные данные в реальном времени и сможем уменьшить $T$ от $T=D$ к $1$ и общая кривая компромисса в конечном итоге становится $TM=N$ с $1\leq T\leq D$ и $P=M$.

Атака Шамира и Бирюкова на поточные шифры

Эта новая идея, представленная в 2000 году, объединяет атаки компромисса Хеллмана и Бэббиджа и Голика для получения новой кривой компромисса с лучшими границами для криптоанализа потокового шифрования. Технику блочного шифрования Хеллмана можно применить к потоковому шифру, используя ту же идею покрытия $N$ пространство точек через матрицы, полученные из нескольких вариантов $f_{i}$ функции $f$ который представляет собой сопоставление внутренних состояний с выходными префиксами. Напомним, что эта компромиссная атака на потоковый шифр успешна, если любое из заданных $D$ выходные префиксы находится в любой из матриц, покрывающих $N$. Это сокращает количество покрытых матрицами точек с $N$ к $N/D$ точки. Это достигается за счет сокращения количества матриц из $t$ к $t/D$ сохраняя при этом $m$ как можно больше (но для этого требуется $t\geq D$ иметь хотя бы одну таблицу).Для этой новой атаки у нас есть $M=mt/D$ потому что мы сократили количество матриц до $t/D$ и то же самое для времени предварительной обработки $P=N/D$. Реальное время, необходимое для атаки, равно $T=(t/D)\cdot t\cdot D=t^{2}$ который является произведением количества матриц, длины каждой итерации и количества доступных точек данных во время атаки.

В конце концов, мы снова используем правило остановки матрицы, чтобы получить кривую компромисса $TM^{2}D^{2}=t^{2}\cdot (m^{2}t^{2}/D^{2})\cdot D^{2}=m^{2}t^{4}=N^{2}$ для $D^{2}\leq T\leq N$ (потому что $t\geq D$).

Атаки на потоковые шифры с низкой

Эта атака, изобретенная Бирюковым , Шамиром и Вагнером , основана на специфической особенности некоторых потоковых шифров: генератор битов претерпевает лишь несколько изменений в своем внутреннем состоянии, прежде чем создать следующий выходной бит. Поэтому мы можем перечислить те особые состояния, которые порождают $k$ нулевые биты для небольших значений $k$ по низкой цене. Но если заставить большое количество выходных битов принимать определенные значения, этот процесс перечисления становится очень дорогим и сложным.Теперь мы можем определить сопротивление выборки потокового шифра как $R=2^{-k}$ с $k$ максимальное значение, при котором такое перечисление возможно.

Пусть потоковый шифр имеет вид $N=2^{n}$ утверждает, что у каждого есть имя полное $n$ биты и соответствующее имя вывода , которое является первым $n$ бит в выходной последовательности битов. Если этот потоковый шифр имеет устойчивость к выборке $R=2^{-k}$, то эффективное перечисление может использовать короткое имя $n-k$ биты для определения особых состояний генератора. Каждое особое состояние с $n-k$ короткое имя имеет соответствующее короткое выходное имя $n-k$ бит, который является выходной последовательностью специального состояния после удаления первого $k$ ведущие биты. Теперь мы можем определить новое отображение в уменьшенном пространстве $NR=2^{n-k}$ точки и это отображение эквивалентно исходному отображению. Если мы позволим $DR\geq 1$, данные реального времени, доступные злоумышленнику, гарантированно будут иметь хотя бы один выход из этих особых состояний. В противном случае мы ослабляем определение особых состояний, чтобы включить больше точек. Если мы заменим $D$ к $DR$ и $N$ к $NR$ в новой атаке Шамира и Бирюкова на компромисс между временем/памятью/данными мы получаем ту же кривую компромисса $TM^{2}D^{2}=N^{2}$ но с $(DR)^{2}\leq T\leq NR$. На самом деле это улучшение, поскольку мы могли бы ослабить нижнюю границу $T$ с $(DR)^{2}$ может быть небольшим до $1$ а это значит, что нашу атаку можно совершить быстрее. Этот метод уменьшает количество дорогостоящих операций доступа к диску с $t$ к $tR$ поскольку мы будем иметь доступ только к специальным $DR$ точек и ускоряет атаку из-за уменьшения количества дорогостоящих дисковых операций.