XXTEA
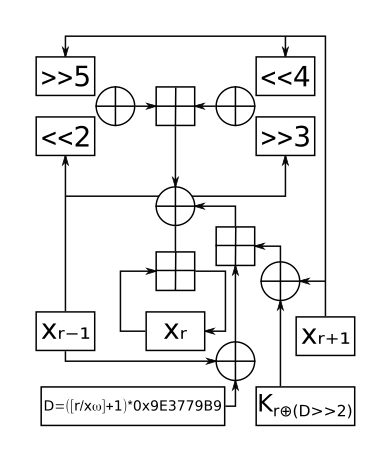 Один раунд XXTEA | |
| Общий | |
|---|---|
| Дизайнеры | Дэвид Уиллер , Роджер Нидэм |
| Впервые опубликовано | октябрь 1998 г. |
| Получено из | Блок ЧАЙ |
| Деталь шифрования | |
| Размеры ключей | 128 бит |
| Размеры блоков | произвольное, не менее двух слов (64 бита) |
| Структура | Несбалансированная сеть Фейстеля |
| Раунды | зависит от размера блока; ~52+6* слов (6-32 полных цикла) |
| Лучший публичный криптоанализ | |
| XXTEA уязвим для атаки с использованием выбранного открытого текста, требующей 2 59 запросы и незначительная работа. [1] | |
В криптографии предназначенный Исправленный блочный TEA (часто называемый XXTEA ) — это блочный шифр, для исправления недостатков исходного Block TEA . [2] [3]
XXTEA уязвим для атаки с использованием выбранного открытого текста, требующей 2 59 запросы и незначительная работа. См. криптоанализ ниже.
Разработчиками шифра . были Роджер Нидэм и Дэвид Уилер из Кембриджской компьютерной лаборатории , а алгоритм был представлен в неопубликованной книге [ нужны разъяснения ] технический отчет в октябре 1998 г. (Wheeler and Needham, 1998). Он не подлежит никаким патентам .
Формально, XXTEA представляет собой последовательный неполный гетерогенный UFN (несбалансированная сеть Фейстеля блочный шифр ) с большим количеством источников. XXTEA работает с блоками переменной длины, размер которых произвольно кратен 32 битам (минимум 64 бита). Количество полных циклов зависит от размера блока, но их не менее шести (для блоков небольшого размера увеличивается до 32). Исходный блок TEA применяет функцию округления XTEA к каждому слову в блоке и аддитивно объединяет его с его крайним левым соседом. Медленная скорость распространения процесса расшифровки была немедленно использована для взлома шифра. Исправленный блок TEA использует более сложную функцию раунда, которая использует обоих непосредственных соседей при обработке каждого слова в блоке.
XXTEA, вероятно, будет более эффективным, чем XTEA, для более длинных сообщений. [ нужна ссылка ]
Needham & Wheeler дают следующие комментарии по поводу использования Block TEA:
Для простоты использования и общей безопасности следует отдавать предпочтение версии с большими блоками, если это применимо, по следующим причинам.
- Одно изменение бита изменит около половины бит всего блока, не оставив места, где начинаются изменения.
- Выбор режима не предусмотрен.
- Даже если используется правильное использование постоянного изменения отправляемых данных (возможно, по номеру сообщения), только идентичные сообщения дают одинаковый результат, и утечка информации минимальна.
- Номер сообщения всегда следует проверять, поскольку эта избыточность является проверкой на возможность принятия случайного сообщения.
- Атаки «разрезание и объединение» кажутся невозможными.
- Если недопустимо иметь очень длинные сообщения, их можно разбить на фрагменты, скажем, по 60 слов и объединить в цепочку аналогично методам, используемым для DES .
Однако из-за неполного характера функции округления два больших зашифрованных текста, состоящих из 53 или более 32-битных слов, идентичных во всех словах, кроме 12, могут быть найдены простым перебором коллизий, требующим 2 96-с.ш. память, 2 Н время и 2 Н +2 96-с.ш. выбранные открытые тексты, другими словами, с общей сложностью времени*памяти 2 96 , что на самом деле 2 размер слова*полные циклы/2 для любого такого шифра. В настоящее время неизвестно, представляют ли такие частичные коллизии какую-либо угрозу безопасности шифра. Восемь полных циклов поднимут планку такого поиска коллизий выше сложности параллельных атак методом перебора. [ нужна ссылка ]
Необычайно малый размер алгоритма XXTEA сделает его жизнеспособным вариантом в ситуациях, когда существуют крайние ограничения, например устаревшие аппаратные системы (возможно, встроенные), где объем доступной оперативной памяти минимален, или, альтернативно, одноплатные компьютеры, такие как Raspberry Pi . Банан Пи или Ардуино .
Криптоанализ [ править ]
Атака, опубликованная в 2010 году Е. Яррковым, представляет собой атаку с выбранным открытым текстом против полного цикла XXTEA с широким блоком, требующую 2 59 запросы на размер блока 212 байт и более и незначительная работа. Он основан на дифференциальном криптоанализе . [1]
Для шифрования «212 байт и более» алгоритм выполняет всего 6 раундов, а тщательно подобранные битовые комбинации позволяют обнаружить и проанализировать лавинный эффект.
Справочный код [ править ]
Исходная формулировка алгоритма Corrected Block TEA, опубликованная Дэвидом Уилером и Роджером Нидхэмом, выглядит следующим образом: [4]
#define DELTA 0x9e3779b9
#define MX (((z>>5^y<<2) + (y>>3^z<<4)) ^ ((sum^y) + (k[p&3^e]^z)))
uint32_t btea(uint32_t* v, ssize_t n, uint32_t* k) {
uint32_t z, y, sum, e, q;
ssize_t p;
if (n > 1) { /* Coding Part */
q = 6 + 52/n;
sum = 0;
z = v[n-1];
for (; q > 0; --q) {
sum += DELTA;
e = (sum >> 2) & 3;
for (p=0; p<n-1; p++) {
y = v[p+1];
z = v[p] += MX;
}
y = v[0];
z = v[n-1] += MX;
}
return 0 ;
} else if (n < -1) { /* Decoding Part */
n = -n;
q = 6 + 52/n;
sum = q*DELTA ;
y = v[0];
for (; q > 0; --q) {
e = (sum >> 2) & 3;
for (p=n-1; p>0; p--) {
z = v[p-1];
y = v[p] -= MX;
}
z = v[n-1];
y = v[0] -= MX;
sum -= DELTA;
}
return 0;
}
return 1;
}
По словам Нидэма и Уиллера:
BTEA будет кодировать или декодировать n слов как один блок, где n > 1.
- v - вектор данных из n слов
- k - ключ из 4 слов
- n отрицательно для декодирования
- если n равно нулю, результат равен 1 и кодирование или декодирование не происходит, в противном случае результат равен нулю
- предполагает 32-битное «длинное» кодирование и декодирование с одинаковым порядком байтов
Обратите внимание, что инициализация z является неопределенным поведением для n < 1, что может привести к ошибке сегментации или другому нежелательному поведению — ее лучше разместить внутри блока «Часть кодирования». Кроме того, в определении MX некоторые программисты предпочитают использовать скобки для уточнения приоритета операторов.
Уточненная версия, включающая эти улучшения, выглядит следующим образом:
#include <stdint.h>
#define DELTA 0x9e3779b9
#define MX (((z>>5^y<<2) + (y>>3^z<<4)) ^ ((sum^y) + (key[(p&3)^e] ^ z)))
void btea(uint32_t *v, int n, uint32_t const key[4]) {
uint32_t y, z, sum;
unsigned p, rounds, e;
if (n > 1) { /* Coding Part */
rounds = 6 + 52/n;
sum = 0;
z = v[n-1];
do {
sum += DELTA;
e = (sum >> 2) & 3;
for (p=0; p<n-1; p++) {
y = v[p+1];
z = v[p] += MX;
}
y = v[0];
z = v[n-1] += MX;
} while (--rounds);
} else if (n < -1) { /* Decoding Part */
n = -n;
rounds = 6 + 52/n;
sum = rounds*DELTA;
y = v[0];
do {
e = (sum >> 2) & 3;
for (p=n-1; p>0; p--) {
z = v[p-1];
y = v[p] -= MX;
}
z = v[n-1];
y = v[0] -= MX;
sum -= DELTA;
} while (--rounds);
}
}
См. также [ править ]
- RC4 : Поточный шифр , который, как и XXTEA, очень прост в реализации.
- XTEA : Блок-предшественник TEA.
- ЧАЙ : предшественник XTEA.
Ссылки [ править ]
- ^ Jump up to: Перейти обратно: а б Элиас Яррков (04 мая 2010 г.). «Криптоанализ XXTEA» . Архив электронной печати по криптологии .
- ^ Мэтью Д. Рассел (27 февраля 2004 г.). «Крошечность: обзор TEA и связанных с ним шифров» . Архивировано из оригинала 12 августа 2007 г.
- ^ Роджер М. Нидэм и Дэвид Дж. Уиллер (октябрь 1997 г.). «Чайные насадки» (PDF) . Компьютерная лаборатория Кембриджского университета, Англия . Проверено 4 июля 2008 г.
- ^ Дэвид Дж. Уиллер и Роджер М. Нидхэм (октябрь 1998 г.). «Поправка к XTEA» (PDF) . Компьютерная лаборатория Кембриджского университета, Англия . Проверено 4 июля 2008 г.