Разделение двоичного пространства

Процесс создания BSP-дерева

В информатике , разделение двоичного пространства ( BSP ) — это метод разделения пространства , который рекурсивно разделяет евклидово пространство на два выпуклых множества используя гиперплоскости в качестве разделов. Этот процесс подразделения приводит к представлению объектов в пространстве в форме древовидной структуры данных, известной как дерево BSP .

Разделение двоичного пространства было разработано в контексте трехмерной компьютерной графики в 1969 году. Структура BSP-дерева полезна при рендеринге, поскольку она может эффективно предоставлять пространственную информацию об объектах сцены, например, об объектах, упорядоченных спереди назад по отношению к зрителю в заданном месте. Другие применения BSP включают: выполнение геометрических операций с фигурами ( конструктивная твердотельная геометрия ) в САПР , обнаружение столкновений в робототехнике и 3D-видеоиграх, трассировка лучей , моделирование виртуальных ландшафтов, и другие приложения, требующие обработки сложных пространственных сцен.

История

• 1969 Шумакер и др. опубликовал отчет, в котором описывалось, как тщательно расположенные плоскости в виртуальной среде можно использовать для ускорения упорядочивания полигонов. В этом методе использовалась когерентность глубины, которая гласит, что многоугольник на дальней стороне плоскости никоим образом не может препятствовать расположению более близкого многоугольника. Это использовалось в авиасимуляторах, созданных GE, а также Evans и Sutherland. Однако создание полигональной организации данных выполнялось дизайнером сцены вручную.

• 1980 Фукс и др. расширил идею Шумакера до представления трехмерных объектов в виртуальной среде, используя плоскости, совпадающие с многоугольниками, для рекурсивного разделения трехмерного пространства. Это обеспечило полностью автоматизированное и алгоритмическое создание иерархической полигональной структуры данных, известной как дерево разделения двоичного пространства (BSP-дерево). Этот процесс представлял собой этап предварительной обработки в автономном режиме, который выполнялся один раз для каждой среды/объекта. Во время выполнения порядок видимости в зависимости от представления создавался путем обхода дерева.
• 1981 Доктор философии Нейлора. В диссертации была полностью разработана как BSP-деревья, так и теоретико-графовый подход с использованием сильно связанных компонентов для видимости перед вычислением, а также связь между двумя методами. Было подчеркнуто, что BSP-деревья как независимая от размерности структура пространственного поиска с применением к определению видимой поверхности. В диссертацию также были включены первые эмпирические данные, демонстрирующие разумность размера дерева и количества новых полигонов (с использованием модели космического корабля "Шаттл").
• 1983 Фукс и др. описал реализацию микрокода алгоритма дерева BSP в системе кадрового буфера Ikonas. Это была первая демонстрация определения видимой поверхности в реальном времени с использованием BSP-деревьев.
• 1987 Тибо и Нэйлор описал, как произвольные многогранники могут быть представлены с использованием дерева BSP в отличие от традиционного b-rep (граничного представления). Это обеспечило твердое представление по сравнению с поверхностным представлением. Операции над многогранниками были описаны с помощью инструмента, позволяющего создавать конструктивную твердотельную геометрию (CSG) в реальном времени. Это был предшественник дизайна уровней BSP с использованием « кистей », представленных в редакторе Quake и подхваченных в редакторе Unreal.
• 1990 г. Нейлор, Аманатидес и Тибо разработали алгоритм объединения двух деревьев BSP для формирования нового дерева BSP из двух исходных деревьев. Это дает множество преимуществ, включая объединение движущихся объектов, представленных BSP-деревьями, со статической средой (также представленной BSP-деревом), очень эффективные операции CSG над многогранниками, точное обнаружение столкновений за O(log n * log n) и правильное упорядочение прозрачных объектов. поверхности, содержащиеся в двух взаимопроникающих объектах (использовалось для эффекта рентгеновского зрения).
• 1990 Теллер и Секвин предложили автономную генерацию потенциально видимых наборов для ускорения определения видимой поверхности в ортогональных 2D-средах.
• 1991 Гордон и Чен [CHEN91] описали эффективный метод выполнения прямого рендеринга из BSP-дерева вместо традиционного обратного подхода. Они использовали специальную структуру данных для эффективной записи уже нарисованных частей экрана и тех, которые еще предстоит отрисовать. Этот алгоритм вместе с описанием BSP Trees в стандартном учебнике компьютерной графики того времени ( Компьютерная графика: принципы и практика ) использовался Джоном Кармаком при создании Doom (видеоигры) .
• 1992 г. Теллера – доктор философии . В диссертации описывается эффективное создание потенциально видимых наборов как этап предварительной обработки для ускорения определения видимой поверхности в реальном времени в произвольных трехмерных полигональных средах. Это использовалось в Quake и внесло значительный вклад в производительность этой игры.
• 1993 г. Нейлор ответил на вопрос, что характеризует хорошее дерево BSP. Он использовал модели ожидаемого случая (а не анализ наихудшего случая) для математического измерения ожидаемой стоимости поиска по дереву и использовал эту меру для построения хороших деревьев BSP. Интуитивно дерево представляет объект в режиме множественного разрешения (точнее, как дерево аппроксимаций). Проведены параллели с кодами Хаффмана и вероятностными двоичными деревьями поиска.
• 1993 Доктор философии Хайдера Радхи. В диссертации были описаны (естественные) методы представления изображений с использованием BSP-деревьев. Сюда входит разработка оптимальной структуры построения BSP-дерева для любого произвольного входного изображения. Эта платформа основана на новом преобразовании изображения, известном как преобразование линии разделения (LPE) с ошибкой наименьшего квадрата (LSE). В диссертации Х. Радхи также были разработаны оптимальная структура сжатия изображений по скорости искажения (RD) и подходы к манипулированию изображениями с использованием BSP-деревьев.

Обзор

Пример рекурсивного квадродерева разделения двоичного пространства для двумерного индекса.

Разделение двоичного пространства — это общий процесс рекурсивного разделения сцены на две части до тех пор, пока разделение не будет удовлетворять одному или нескольким требованиям. Его можно рассматривать как обобщение других пространственных древовидных структур, таких как k -d-деревья и квадродеревья , в которых гиперплоскости, разделяющие пространство, могут иметь любую ориентацию, а не быть выровнены по осям координат, как в k -d-деревьях или квадродеревья. При использовании в компьютерной графике для рендеринга сцен, состоящих из плоских многоугольников , плоскости разделения часто выбираются так, чтобы они совпадали с плоскостями, определяемыми многоугольниками в сцене.

Конкретный выбор плоскости разбиения и критерия завершения процесса разбиения варьируется в зависимости от назначения дерева BSP. Например, при рендеринге компьютерной графики сцена делится до тех пор, пока каждый узел дерева BSP не будет содержать только полигоны, которые можно визуализировать в произвольном порядке. Таким образом, при использовании отсеивания обратной грани каждый узел содержит выпуклый набор полигонов, тогда как при рендеринге двусторонних полигонов каждый узел дерева BSP содержит только полигоны в одной плоскости. При обнаружении столкновений или трассировке лучей сцена может быть разделена на примитивы , на которых можно легко выполнить проверку столкновений или пересечений лучей.

Разделение двоичного пространства возникло из-за необходимости компьютерной графики быстро рисовать трехмерные сцены, состоящие из многоугольников. Простым способом рисования таких сцен является алгоритм художника , который создает полигоны в порядке удаления от зрителя, задом наперед, закрашивая фон и предыдущие полигоны с каждым более близким объектом. У этого подхода есть два недостатка: время, необходимое для сортировки полигонов в обратном порядке, и возможность ошибок при перекрытии полигонов. Фукс и соавторы показали, что построение BSP-дерева решает обе эти проблемы, предоставляя быстрый метод сортировки полигонов относительно заданной точки обзора (линейный по количеству полигонов в сцене) и подразделяя перекрывающиеся полигоны, чтобы избежать ошибок, которые могут возникнуть при работе художника. алгоритм. Недостатком разделения двоичного пространства является то, что создание дерева BSP может занять много времени. Поэтому обычно он выполняется один раз для статической геометрии на этапе предварительного расчета перед рендерингом или другими операциями в реальном времени на сцене. Затраты на построение BSP-дерева затрудняют и делают неэффективным прямое перемещение объектов в дерево.

Поколение

Каноническое использование дерева BSP предназначено для рендеринга многоугольников (двусторонних, то есть без отсеивания обратной стороны ) с помощью алгоритма художника. Каждый многоугольник имеет лицевую и обратную стороны, которые могут выбираться произвольно и влияют только на структуру дерева, но не на требуемый результат. Такое дерево строится из неотсортированного списка всех полигонов сцены. Рекурсивный алгоритм построения дерева BSP из этого списка полигонов:

1. Выберите многоугольник P из списка.
2. Создайте узел N в дереве BSP и добавьте P в список полигонов в этом узле.
3. Для каждого другого полигона в списке:
   1. Если этот многоугольник полностью находится перед плоскостью, содержащей , переместите этот многоугольник в список узлов перед P. P
   2. Если этот многоугольник полностью находится за плоскостью, содержащей , переместите этот многоугольник в список узлов за P. P
   3. Если этот многоугольник пересекается плоскостью, содержащей , разделите его на два многоугольника и переместите их в соответствующие списки многоугольников позади и перед P. P
   4. Если этот многоугольник лежит в плоскости, содержащей P , добавьте его в список многоугольников в N. узле
4. Примените этот алгоритм к списку многоугольников перед P .
5. Примените этот алгоритм к списку многоугольников позади P .

Следующая диаграмма иллюстрирует использование этого алгоритма для преобразования списка линий или многоугольников в дерево BSP. На каждом из восьми шагов (i-viii) описанный выше алгоритм применяется к списку строк и к дереву добавляется один новый узел.

	Начните со списка линий (или в 3D многоугольников), составляющих сцену. На древовидных диаграммах списки обозначаются прямоугольниками с закругленными углами, а узлы дерева BSP — кружками. На пространственной диаграмме линий направление, выбранное в качестве «передней» линии, обозначается стрелкой.
я.	Следуя шагам алгоритма выше, Мы выбираем строку A из списка и... ...добавьте его в узел. Мы разделяем оставшиеся строки в списке на те, что перед A (т.е. B2, C2, D2) и те, что позади (B1, C1, D1). Сначала мы обрабатываем строки перед A (на шагах ii–v),... ... за которыми следуют те, кто стоит сзади (шаги vi – vii).
ii.	Теперь мы применим алгоритм к списку строк перед A (содержащему B2, C2, D2). Мы выбираем строку B2, добавляем ее в узел и разбиваем остальную часть списка на те строки, которые находятся перед B2 (D2), и те, которые находятся за ним (C2, D3).
iii.	Выберите линию D2 из списка строк перед B2 и A. Это единственная линия в списке, поэтому после добавления ее в узел больше ничего делать не нужно.
iv.	Мы закончили с линиями перед B2, поэтому рассмотрим линии за B2 (C2 и D3). Выберите один из них (C2), добавьте его в узел и поместите другую строку из списка (D3) в список строк перед C2.
v.	Теперь посмотрите на список строк перед C2. Существует только одна линия (D3), поэтому добавьте ее в узел и продолжайте.
мы.	Теперь мы добавили все строки перед A в дерево BSP, поэтому начинаем со списка строк после A. Выбрав строку (B1) из этого списка, мы добавляем B1 к узлу и разделяем остаток список на строки перед B1 (т.е. D1) и строки за B1 (т.е. C1).
VII.	Сначала обрабатывается список строк перед B1, D1 — единственная строка в этом списке, поэтому добавьте ее в узел и продолжайте.
viii.	Далее, взглянув на список строк за B1, можно увидеть, что единственной строкой в ​​этом списке является C1, поэтому добавьте ее в узел, и дерево BSP будет завершено.

Конечное количество полигонов или линий в дереве часто больше (иногда намного больше). ), чем исходный список, поскольку линии или многоугольники, пересекающие плоскость разбиения, должны быть разделены на две части. Желательно минимизировать это увеличение, но при этом сохранить разумный баланс в конечном дереве. Поэтому выбор того, какой многоугольник или линия будет использоваться в качестве плоскости разбиения (на этапе 1 алгоритма), важен для создания эффективного BSP-дерева.

Обход

Дерево BSP просматривается за линейное время в порядке, определяемом конкретной функцией дерева. Опять же, используя пример рендеринга двусторонних многоугольников с использованием алгоритма художника, для правильного рисования многоугольника P все многоугольники за плоскостью P чтобы сначала были нарисованы , затем многоугольник P и, наконец, многоугольники перед P. необходимо , Если этот порядок отрисовки соблюдается для всех полигонов сцены, то вся сцена отображается в правильном порядке. Эту процедуру можно реализовать путем рекурсивного обхода дерева BSP с использованием следующего алгоритма. Из заданного места просмотра V для визуализации дерева BSP:

1. Если текущий узел является листовым узлом, визуализируйте полигоны в текущем узле.
2. В противном случае, если точка просмотра V находится перед текущим узлом:
   1. Отобразите дочернее дерево BSP, содержащее полигоны позади текущего узла.
   2. Рендеринг полигонов в текущем узле
   3. Отобразить дочернее дерево BSP, содержащее полигоны перед текущим узлом.
3. В противном случае, если точка просмотра V находится за текущим узлом:
   1. Отобразить дочернее дерево BSP, содержащее полигоны перед текущим узлом.
   2. Рендеринг полигонов в текущем узле
   3. Отобразите дочернее дерево BSP, содержащее полигоны позади текущего узла.
4. В противном случае точка просмотра V должна находиться точно в плоскости, связанной с текущим узлом. Затем:
   1. Отобразить дочернее дерево BSP, содержащее полигоны перед текущим узлом.
   2. Отобразите дочернее дерево BSP, содержащее полигоны позади текущего узла.

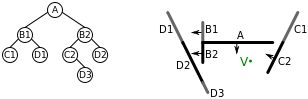
Рекурсивное применение этого алгоритма к сгенерированному выше дереву BSP приводит к следующим шагам:

• Алгоритм сначала применяется к корневому узлу дерева, A. узлу V находится перед узлом A , поэтому мы сначала применяем алгоритм к дочернему дереву BSP, содержащему многоугольники за A.
  • Это дерево имеет корневой узел B1 . V находится за B1 , поэтому сначала мы применяем алгоритм к дочернему дереву BSP, содержащему многоугольники перед B1 :
    • Это дерево является всего лишь конечным узлом D1 многоугольник D1 . , поэтому визуализируется
  • Затем мы визуализируем многоугольник B1 .
  • Затем мы применяем алгоритм к дочернему дереву BSP, содержащему многоугольники за B1 :
    • Это дерево представляет собой всего лишь листовой узел C1 многоугольник C1 . , поэтому визуализируется
• Затем мы рисуем многоугольники A
• Затем мы применяем алгоритм к дочернему дереву BSP, содержащему многоугольники перед A.
  • Это дерево имеет корневой узел B2 . V находится за B2 , поэтому сначала мы применяем алгоритм к дочернему дереву BSP, содержащему полигоны перед B2 :
    • Это дерево является всего лишь конечным узлом D2 многоугольник D2 . , поэтому визуализируется
  • Затем мы визуализируем многоугольник B2 .
  • Затем мы применяем алгоритм к дочернему дереву BSP, содержащему многоугольники за B2 :
    • Это дерево имеет корневой узел C2 . V находится перед C2 , поэтому сначала мы применим алгоритм к дочернему дереву BSP, содержащему многоугольники позади C2 . Однако такого дерева нет, поэтому продолжаем.
    • Мы визуализируем многоугольник C2 .
    • Мы применяем алгоритм к дочернему дереву BSP, содержащему полигоны перед C2.
      • Это дерево является всего лишь конечным узлом D3 многоугольник D3 . , поэтому визуализируется

Дерево просматривается за линейное время и отображает полигоны в порядке от дальнего к близкому ( D1 , B1 , C1 , A , D2 , B2 , C2 , D3 ), подходящем для алгоритма художника.

Приложение

Деревья BSP часто используются в 3D- видеоиграх , особенно в шутерах от первого лица и в играх, действие которых происходит в помещении. Игровые движки, использующие деревья BSP, включают движки Doom (id Tech 1) , Quake (вариант id Tech 2) , GoldSrc и Source . В них BSP-деревья, содержащие статическую геометрию сцены, часто используются вместе с Z-буфером , чтобы правильно объединить подвижные объекты, такие как двери и персонажи, с фоновой сценой. Хотя разделение двоичного пространства обеспечивает удобный способ хранения и извлечения пространственной информации о полигонах в сцене, оно не решает проблему определения видимой поверхности . Однако деревья BSP применяются для сжатия изображений.

См. также

• кд дерево
• Октри
• Четырехдерево
• Иерархическая кластеризация — альтернативный способ разделения данных 3D-модели для эффективного рендеринга.
• Гильотинная резка

Дополнительные ссылки

• Нейлор, Б.; Аманатидес, Дж.; Тибо, В. (август 1990 г.). «Объединение деревьев BSP дает операции над многогранными множествами». ACM SIGGRAPH Компьютерная графика . 24 (4): 115–124. CiteSeerX   10.1.1.69.292 . дои : 10.1145/97880.97892 .
• Нейлор, Б. (май 1993 г.). «Построение хороших деревьев разбиения» . Графический интерфейс . CiteSeerX   10.1.1.16.4432 .
• Чен, С.; Гордон, Д. (сентябрь 1991 г.). «Отображение деревьев BSP спереди назад». IEEE Компьютерная графика и приложения . 11 (5): 79–85. дои : 10.1109/38.90569 . S2CID   19056967 .
• Радха, Х.; Леонарди, Р.; Веттерли, М.; Нейлор, Б. (1991). «Двоичное представление изображений в виде дерева разбиения пространства» . Журнал визуальных коммуникаций и обработки изображений . 2 (3): 201–221. дои : 10.1016/1047-3203(91)90023-9 .
• Радха, HMS (1993). Эффективное представление изображений с использованием деревьев разделения двоичного пространства (доктор философии). Колумбийский университет. ОСЛК   30775044 .
• Радха, HMS (1994). «Эффективное представление изображений с использованием деревьев разбиения двоичного пространства». Обработка сигналов . 35 (2): 174–181. дои : 10.1016/0165-1684(94)90047-7 .
• Радха, Х.; Веттерли, М.; Леонарди, Р. (декабрь 1996 г.). «Сжатие изображений с использованием деревьев разбиения двоичного пространства» . Транзакции IEEE при обработке изображений . 5 (12): 1610–24. Бибкод : 1996ITIP....5.1610R . дои : 10.1109/83.544569 . ПМИД   18290079 . https://ui.adsabs.harvard.edu/abs/1996ITIP....5.1610R/abstract
• Зима, А.С. (апрель 1999 г.). «Исследование рендеринга трехмерных полигонов в реальном времени с использованием bsp-деревьев». CiteSeerX   10.1.1.11.9725 .
• де Берг, М .; ван Кревелд, М .; Овермарс, М .; Шварцкопф, О. (2000). «§12: Бинарные разделы пространства». Вычислительная геометрия (2-е изд.). Спрингер-Верлаг . стр. 251–265. ISBN  978-3-540-65620-3 . Описывает рандомизированный алгоритм художника.
• Эриксон, Кристер (2005). «8. Иерархии деревьев BSP» . Обнаружение столкновений в реальном времени . Серия Моргана Кауфмана по интерактивным 3D-технологиям. Морган Кауфманн. стр. 349–382. ISBN  1-55860-732-3 .

Внешние ссылки

• Нейлор, Б.Ф. (2005). «Учебное пособие по деревьям разбиения двоичного пространства» .
• Презентация деревьев BSP
• Еще одна презентация деревьев BSP
• Java-апплет, демонстрирующий процесс создания дерева.
• Магистерская диссертация о создании BSP
• Деревья BSP: теория и реализация
• БСП в 3D пространстве
• Graphics Gems V: прогулка по BSP-деревьям