Перекрестная энтропия

В теории информации перекрёстная энтропия между двумя распределениями вероятностей $p$ и $q$, по одному и тому же базовому набору событий, измеряет среднее количество битов, необходимое для идентификации события, взятого из набора, когда схема кодирования, используемая для набора, оптимизирована для предполагаемого распределения вероятностей. $q$, а не истинное распределение $p$.

Определение

Перекрестная энтропия распределения $q$ относительно распределения $p$ по заданному множеству определяется следующим образом:

$H(p,q)=-\operatorname {E} _{p}[\log q]$,

где $E_{p}[\cdot ]$ — оператор ожидаемого значения относительно распределения $p$.

Определение можно сформулировать с использованием расхождения Кульбака – Лейблера. $D_{\mathrm {KL} }(p\parallel q)$, расхождение $p$ от $q$ (также известная как энтропия относительная $p$ относительно $q$).

$H(p,q)=H(p)+D_{\mathrm {KL} }(p\parallel q),$

где $H(p)$ это энтропия ​ $p$.

Для дискретных распределений вероятностей $p$ и $q$ с той же поддержкой ${\mathcal {X}}$, это означает

$H(p,q)=-\sum _{x\in {\mathcal {X}}}p(x)\,\log q(x)$. ( Уравнение 1 )

ситуация и для непрерывных Аналогичная распределений. Мы должны предположить, что $p$ и $q$ относительно абсолютно непрерывны некоторой эталонной меры $r$ (обычно $r$ является мерой Лебега на борелевской σ-алгебре ). Позволять $P$ и $Q$ — функции плотности вероятности $p$ и $q$ относительно $r$. Затем

$-\int _{\mathcal {X}}P(x)\,\log Q(x)\,\mathrm {d} \ \!x=\operatorname {E} _{p}[-\log Q],$

и поэтому

$H(p,q)=-\int _{\mathcal {X}}P(x)\,\log Q(x)\,\mathrm {d} \ \!x$. ( Уравнение 2 )

Примечание: Обозначения $H(p,q)$ также используется для другого понятия - совместной энтропии $p$ и $q$.

Мотивация

В теории информации теорема Крафта-Макмиллана устанавливает, что любая непосредственно декодируемая схема кодирования для кодирования сообщения для идентификации одного значения $x_{i}$ из набора возможностей $\{x_{1},\ldots ,x_{n}\}$ можно рассматривать как представление неявного распределения вероятностей $q(x_{i})=\left({\frac {1}{2}}\right)^{\ell _{i}}$ над $\{x_{1},\ldots ,x_{n}\}$, где $\ell _{i}$ длина кода для $x_{i}$ в битах. Следовательно, перекрестную энтропию можно интерпретировать как ожидаемую длину сообщения на единицу данных при неправильном распределении. $q$ предполагается, в то время как данные фактически следуют распределению $p$. Вот почему математическое ожидание принимается за истинное распределение вероятностей. $p$ и не $q.$ Действительно, ожидаемая длина сообщения при истинном распределении $p$ является

$$\operatorname {E} _{p}[\ell ]=-\operatorname {E} _{p}\left[{\frac {\ln {q(x)}}{\ln(2)}}\right]=-\operatorname {E} _{p}\left[\log _{2}{q(x)}\right]=-\sum _{x_{i}}p(x_{i})\,\log _{2}q(x_{i})=-\sum _{x}p(x)\,\log _{2}q(x)=H(p,q).$$

Оценка

Во многих ситуациях необходимо измерить перекрестную энтропию, но распределение $p$ неизвестно. Примером является языковое моделирование , где модель создается на основе обучающего набора. $T$, а затем ее перекрестная энтропия измеряется на тестовом наборе, чтобы оценить, насколько точно модель прогнозирует тестовые данные. В этом примере $p$ это истинное распределение слов в любом корпусе, и $q$ — это распределение слов, предсказанное моделью. Поскольку истинное распределение неизвестно, перекрестную энтропию невозможно вычислить напрямую. В этих случаях оценка перекрестной энтропии рассчитывается по следующей формуле:

$H(T,q)=-\sum _{i=1}^{N}{\frac {1}{N}}\log _{2}q(x_{i})$

где $N$ - размер тестового набора, и $q(x)$ это вероятность события $x$ оценивается по обучающему набору. Другими словами, $q(x_{i})$ — это оценка вероятности модели того, что i-е слово текста является $x_{i}$. Сумма усредняется по $N$ слова теста. Это Монте-Карло , где тестовый набор рассматривается как образцы из оценка истинной перекрестной энтропии методом $p(x)$.

Отношение к максимальной вероятности

Перекрестная энтропия возникает в задачах классификации при введении логарифма под видом функции логарифма правдоподобия .

Раздел посвящен теме оценки вероятности различных возможных дискретных исходов. Для этого обозначим параметризованное семейство распределений через $q_{\theta }$, с $\theta$ с учетом усилий по оптимизации. Рассмотрим данную конечную последовательность $N$ ценности $x_{i}$ из обучающей выборки, полученной в результате условно независимой выборки. Вероятность, присвоенная любому рассматриваемому параметру $\theta$ модели тогда определяется произведением по всем вероятностям $q_{\theta }(X=x_{i})$.Возможны повторения, приводящие к равным коэффициентам в продукте. Если количество вхождений значения равно $x_{i}$ (для некоторого индекса $i$) обозначается $\#x_{i}$, то частота этого значения равна $\#x_{i}/N$. Обозначим последнее через $p(X=x_{i})$, поскольку его можно понимать как эмпирическое приближение к распределению вероятностей, лежащему в основе сценария. Далее обозначим через $PP:={\mathrm {e} }^{H(p,q_{\theta })}$ недоумение , которое можно рассматривать как равное ${\textstyle \prod _{x_{i}}}q_{\theta }(X=x_{i})^{-p(X=x_{i})}$ по правилам расчета логарифма и где произведение превышает значения без двойного счета. Так

${\mathcal {L}}(\theta ;{\mathbf {x} })=\prod _{i}q_{\theta }(X=x_{i})=\prod _{x_{i}}q_{\theta }(X=x_{i})^{\#x_{i}}=PP^{-N}={\mathrm {e} }^{-N\cdot H(p,q_{\theta })}$

или

$\log {\mathcal {L}}(\theta ;{\mathbf {x} })=-N\cdot H(p,q_{\theta }).$

Поскольку логарифм — монотонно возрастающая функция , он не влияет на экстремизацию. Итак, заметьте, что максимизация правдоподобия означает минимизацию перекрестной энтропии.

Минимизация перекрестной энтропии

Основная статья: Метод перекрестной энтропии

Минимизация перекрестной энтропии часто используется при оптимизации и оценке вероятности редких событий. При сравнении распределения $q$ против фиксированного эталонного распределения $p$, кросс-энтропия и KL-дивергенция идентичны с точностью до аддитивной константы (поскольку $p$ фиксировано): Согласно неравенству Гиббса , оба принимают свои минимальные значения, когда $p=q$, что $0$ для KL-расхождения, и $\mathrm {H} (p)$ для перекрестной энтропии. В инженерной литературе принцип минимизации KL-дивергенции (« Принцип минимальной дискриминационной информации » Кульбака) часто называют принципом минимальной перекрестной энтропии (MCE), или Minxent .

Однако, как обсуждается в статье « Расхождение Кульбака – Лейблера» , иногда распределение $q$ - фиксированное априорное эталонное распределение, а распределение $p$ оптимизирован так, чтобы быть как можно ближе к $q$ насколько это возможно, с учетом некоторых ограничений. В этом случае две минимизации не эквивалентны. Это привело к некоторой двусмысленности в литературе: некоторые авторы пытались разрешить это несоответствие, вновь заявляя, что кросс-энтропия $D_{\mathrm {KL} }(p\parallel q)$, скорее, чем $H(p,q)$. Фактически, перекрестная энтропия — это другое название относительной энтропии ; см. Ковер и Томас и Хорошо. С другой стороны, $H(p,q)$ не согласуется с литературой и может вводить в заблуждение.

Функция перекрестных энтропийных потерь и логистическая регрессия

Перекрестная энтропия может использоваться для определения функции потерь в машинном обучении и оптимизации . Мао, Мори и Чжун (2023) дают обширный анализ свойств семейства функций перекрестных энтропийных потерь в машинах.обучение, включая гарантии теоретического обучения и расширениесостязательное обучение. Истинная вероятность $p_{i}$ - истинная метка, а данное распределение $q_{i}$ — прогнозируемое значение текущей модели. Это также известно как логарифмические потери (или логарифмические потери). или логистические потери ); термины «логарифмические потери» и «перекрестные энтропийные потери» используются как взаимозаменяемые.

Более конкретно, рассмотрим модель бинарной регрессии , которую можно использовать для классификации наблюдений на два возможных класса (часто обозначаемых просто как $0$ и $1$). Выходные данные модели для данного наблюдения с учетом вектора входных признаков. $x$, можно интерпретировать как вероятность, которая служит основой для классификации наблюдения. В логистической регрессии вероятность моделируется с помощью логистической функции $g(z)=1/(1+e^{-z})$ где $z$ — некоторая функция входного вектора $x$, обычно просто линейная функция. Вероятность выхода $y=1$ дается

$q_{y=1}={\hat {y}}\equiv g(\mathbf {w} \cdot \mathbf {x} )={\frac {1}{1+e^{-\mathbf {w} \cdot \mathbf {x} }}},$

где вектор весов $\mathbf {w}$ оптимизируется с помощью некоторого подходящего алгоритма, такого как градиентный спуск . Аналогично, дополнительная вероятность найти выход $y=0$ просто дается

$q_{y=0}=1-{\hat {y}}.$

Установив наши обозначения, $p\in \{y,1-y\}$ и $q\in \{{\hat {y}},1-{\hat {y}}\}$, мы можем использовать перекрестную энтропию, чтобы получить меру несходства между $p$ и $q$:

$H(p,q)\ =\ -\sum _{i}p_{i}\log q_{i}\ =\ -y\log {\hat {y}}-(1-y)\log(1-{\hat {y}}).$

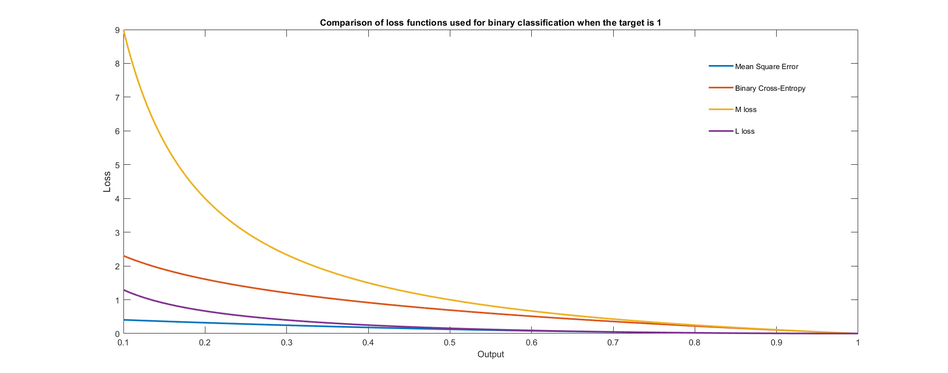
На графике показаны различные функции потерь, которые можно использовать для обучения двоичного классификатора. Показан только случай, когда целевой выход равен 1. Замечено, что потери равны нулю, когда целевое значение равно выходному значению, и увеличиваются по мере того, как выходные данные становятся все более неверными.

Логистическая регрессия обычно оптимизирует потери журнала для всех наблюдений, на которых она обучается, что аналогично оптимизации средней перекрестной энтропии в выборке. Для обучения также можно использовать другие функции потерь, которые по-разному наказывают за ошибки, что приводит к получению моделей с разной точностью окончательного теста. Например, предположим, что у нас есть $N$ образцы, каждый из которых индексируется $n=1,\dots ,N$. Среднее значение функции потерь тогда определяется следующим образом:

${\begin{aligned}J(\mathbf {w} )\ &=\ {\frac {1}{N}}\sum _{n=1}^{N}H(p_{n},q_{n})\ =\ -{\frac {1}{N}}\sum _{n=1}^{N}\ {\bigg [}y_{n}\log {\hat {y}}_{n}+(1-y_{n})\log(1-{\hat {y}}_{n}){\bigg ]}\,,\end{aligned}}$

где ${\hat {y}}_{n}\equiv g(\mathbf {w} \cdot \mathbf {x} _{n})=1/(1+e^{-\mathbf {w} \cdot \mathbf {x} _{n}})$, с $g(z)$ логистическая функция прежняя.

Логистические потери иногда называют кросс-энтропийными потерями. Это также известно как потеря журнала. (В этом случае двоичная метка часто обозначается {−1,+1}. )

Примечание. Градиент потери перекрестной энтропии для логистической регрессии такой же, как градиент потери квадрата ошибки для линейной регрессии . То есть определить

$X^{T}={\begin{pmatrix}1&x_{11}&\dots &x_{1p}\\1&x_{21}&\cdots &x_{2p}\\\vdots &\vdots &&\vdots \\1&x_{n1}&\cdots &x_{np}\\\end{pmatrix}}\in \mathbb {R} ^{n\times (p+1)},$

${\hat {y_{i}}}={\hat {f}}(x_{i1},\dots ,x_{ip})={\frac {1}{1+\exp(-\beta _{0}-\beta _{1}x_{i1}-\dots -\beta _{p}x_{ip})}},$

$L({\boldsymbol {\beta }})=-\sum _{i=1}^{N}\left[y_{i}\log {\hat {y}}_{i}+(1-y_{i})\log(1-{\hat {y}}_{i})\right].$

Тогда у нас есть результат

${\frac {\partial }{\partial {\boldsymbol {\beta }}}}L({\boldsymbol {\beta }})=X^{T}({\hat {Y}}-Y).$

Доказательство состоит в следующем. Для любого ${\hat {y}}_{i}$, у нас есть

${\frac {\partial }{\partial \beta _{0}}}\ln {\frac {1}{1+e^{-\beta _{0}+k_{0}}}}={\frac {e^{-\beta _{0}+k_{0}}}{1+e^{-\beta _{0}+k_{0}}}},$

${\frac {\partial }{\partial \beta _{0}}}\ln \left(1-{\frac {1}{1+e^{-\beta _{0}+k_{0}}}}\right)={\frac {-1}{1+e^{-\beta _{0}+k_{0}}}},$

${\begin{aligned}{\frac {\partial }{\partial \beta _{0}}}L({\boldsymbol {\beta }})&=-\sum _{i=1}^{N}\left[{\frac {y_{i}\cdot e^{-\beta _{0}+k_{0}}}{1+e^{-\beta _{0}+k_{0}}}}-(1-y_{i}){\frac {1}{1+e^{-\beta _{0}+k_{0}}}}\right]\\&=-\sum _{i=1}^{N}\left[y_{i}-{\hat {y}}_{i}\right]=\sum _{i=1}^{N}({\hat {y}}_{i}-y_{i}),\end{aligned}}$

${\frac {\partial }{\partial \beta _{1}}}\ln {\frac {1}{1+e^{-\beta _{1}x_{i1}+k_{1}}}}={\frac {x_{i1}e^{k_{1}}}{e^{\beta _{1}x_{i1}}+e^{k_{1}}}},$

${\frac {\partial }{\partial \beta _{1}}}\ln \left[1-{\frac {1}{1+e^{-\beta _{1}x_{i1}+k_{1}}}}\right]={\frac {-x_{i1}e^{\beta _{1}x_{i1}}}{e^{\beta _{1}x_{i1}}+e^{k_{1}}}},$

${\frac {\partial }{\partial \beta _{1}}}L({\boldsymbol {\beta }})=-\sum _{i=1}^{N}x_{i1}(y_{i}-{\hat {y}}_{i})=\sum _{i=1}^{N}x_{i1}({\hat {y}}_{i}-y_{i}).$

Подобным образом мы в конечном итоге получаем желаемый результат.

Измененная перекрестная энтропия

Может быть полезно обучить ансамбль моделей, которые имеют разнообразие, так что при их объединении точность их прогнозирования увеличивается. Если предположить, что это простой ансамбль $K$ классификаторы собираются путем усреднения выходных данных, тогда исправленная кросс-энтропия определяется выражением

$e^{k}=H(p,q^{k})-{\frac {\lambda }{K}}\sum _{j\neq k}H(q^{j},q^{k})$

где $e^{k}$ представляет собой функцию стоимости $k^{th}$ классификатор, $q^{k}$ - выходная вероятность $k^{th}$ классификатор, $p$ - истинная вероятность, которую необходимо оценить, и $\lambda$ — это параметр от 0 до 1, определяющий «разнообразие», которое мы хотели бы установить в ансамбле. Когда $\lambda =0$ мы хотим, чтобы каждый классификатор работал наилучшим образом независимо от ансамбля и времени $\lambda =1$ нам бы хотелось, чтобы классификатор был как можно более разнообразным.

См. также

• Метод перекрестной энтропии
• Логистическая регрессия
• Условная энтропия
• Расстояние Кульбака – Лейблера
• Оценка максимального правдоподобия
• Взаимная информация

Дальнейшее чтение

• де Бур, Крозе, Д.П., Маннор, С. и Рубинштейн, Р.Ю. (2005). Учебное пособие по методу перекрестной энтропии . Анналы исследования операций 134 (1), 19–67.