Машина Этвуда

Иллюстрация машины Этвуда, 1905 год.

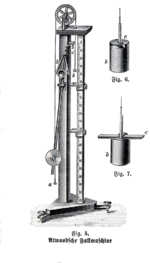
Машина Этвуда (или машина Этвуда ) была изобретена в 1784 году английским математиком Джорджем Этвудом в качестве лабораторного эксперимента по проверке механических законов движения с постоянным ускорением . Машина Этвуда — это обычная демонстрация в классе, используемая для иллюстрации принципов классической механики .

Идеальная машина Атвуда состоит из двух объектов масс m ₁ и m ₂ , соединенных нерастяжимой невесомой нитью над идеальным немассовым шкивом .

Обе массы испытывают равномерное ускорение. Когда m ₁ = m ₂ , машина находится в нейтральном равновесии независимо от положения грузов.

Уравнение постоянного ускорения

Схемы свободного тела двух висящих масс машины Этвуда. Наше соглашение о знаках , изображенное векторами , ускорения заключается в том, что m ₁ ускоряется вниз, а m ₂ ускоряется вверх, как это было бы в случае, если m ₁ > m _2.

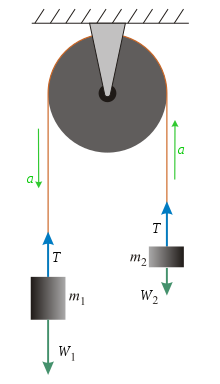
Уравнение ускорения можно получить путем анализа сил.Предполагая безмассовую, нерастяжимую струну и идеальный безмассовый блок, единственными силами, которые следует учитывать, являются: сила натяжения ( T ) и вес двух масс ( W ₁ и W ₂ ). Чтобы найти ускорение, рассмотрим силы, действующие на каждую отдельную массу. Используя второй закон Ньютона (с знаках соглашением о $m_{1}>m_{2}$) вывести систему уравнений для ускорения ( a ).

В качестве соглашения о знаках предположим, что a положительно, когда направлено вниз для $m_{1}$ и вверх для $m_{2}$. Вес $m_{1}$ и $m_{2}$ это просто $W_{1}=m_{1}g$ и $W_{2}=m_{2}g$ соответственно.

Силы, действующие на m ₁ : $$m_{1}g-T=m_{1}a$$Силы, действующие на м ₂ : $$T-m_{2}g=m_{2}a$$и добавление двух предыдущих уравнений дает $$m_{1}g-m_{2}g=m_{1}a+m_{2}a,$$и итоговая формула ускорения $$a=g{\frac {m_{1}-m_{2}}{m_{1}+m_{2}}}$$

Машина Этвуда иногда используется для иллюстрации лагранжевого метода вывода уравнений движения.

Уравнение напряжения

Может быть полезно знать уравнение натяжения струны . Чтобы оценить натяжение, подставьте уравнение ускорения в любое из двух уравнений силы.

$$a=g{m_{1}-m_{2} \over m_{1}+m_{2}}$$

Например, подставив в $m_{1}a=m_{1}g-T$, приводит к $$T={2gm_{1}m_{2} \over m_{1}+m_{2}}={2g \over 1/m_{1}+1/m_{2}}=m_{h}\,g$$где $m_{h}={\frac {2m_{1}m_{2}}{m_{1}+m_{2}}}$ является средним гармоническим значением двух масс. Числовое значение $m_{h}$ ближе к меньшей из двух масс.

Уравнения шкива с инерцией и трением

При очень небольшой разнице масс между m ₁ и m ₂ инерцией вращения I шкива радиуса r нельзя пренебрегать . Угловое ускорение шкива задается условием прилипания: $$\alpha ={\frac {a}{r}},$$где $\alpha$ это угловое ускорение. чистый крутящий момент Тогда составит: $$\tau _{\mathrm {net} }=\left(T_{1}-T_{2}\right)r-\tau _{\mathrm {friction} }=I\alpha$$

Объединив второй закон Ньютона для висящих масс и вычислив T ₁ , T ₂ и a , мы получаем:

Ускорение: $$a={{g(m_{1}-m_{2})-{\tau _{\mathrm {friction} } \over r}} \over {m_{1}+m_{2}+{{I} \over {r^{2}}}}}$$

Натяжение в ближайшем сегменте струны, м ₁ : $$T_{1}={{m_{1}g\left(2m_{2}+{\frac {I}{r^{2}}}+{\frac {\tau _{\mathrm {friction} }}{rg}}\right)} \over {m_{1}+m_{2}+{\frac {I}{r^{2}}}}}$$

Натяжение в ближайшем сегменте струны, м ₂ : $$T_{2}={{m_{2}g\left(2m_{1}+{\frac {I}{r^{2}}}+{\frac {\tau _{\mathrm {friction} }}{rg}}\right)} \over {m_{1}+m_{2}+{\frac {I}{r^{2}}}}}$$

Если трение подшипника пренебрежимо мало (но не инерция шкива и натяжение струны на ободе шкива), эти уравнения упрощаются до следующих результатов:

Ускорение: $$a={{g\left(m_{1}-m_{2}\right)} \over {m_{1}+m_{2}+{\frac {I}{r^{2}}}}}$$

Натяжение в ближайшем сегменте струны, м ₁ : $$T_{1}={{m_{1}g\left(2m_{2}+{\frac {I}{r^{2}}}\right)} \over {m_{1}+m_{2}+{\frac {I}{r^{2}}}}}$$

Натяжение в ближайшем сегменте струны, м ₂ : $$T_{2}={{m_{2}g\left(2m_{1}+{\frac {I}{r^{2}}}\right)} \over {m_{1}+m_{2}+{\frac {I}{r^{2}}}}}$$

Практическая реализация

На оригинальных иллюстрациях Этвуда показано, что ось главного шкива опирается на обода еще четырех колес, чтобы минимизировать силы трения от подшипников . Многие исторические реализации машины следуют этой конструкции.

Лифт с противовесом приближается к идеальной машине Этвуда и тем самым освобождает приводной двигатель от нагрузки по удержанию кабины лифта — ему приходится преодолевать лишь разницу веса и инерцию двух масс. Тот же принцип используется для фуникулера с двумя соединенными вагонами на наклонных путях и для лифтов на Эйфелевой башне, которые уравновешивают друг друга. Еще одним примером являются горнолыжные подъемники, где гондолы перемещаются по замкнутой (непрерывной) системе блоков вверх и вниз по горе. Лыжный подъемник аналогичен подъемнику с противовесом, но с ограничивающей силой, создаваемой тросом в вертикальном измерении, что обеспечивает работу как в горизонтальном, так и в вертикальном измерениях. Лодочные подъемники — это еще один тип лифтовой системы с противовесом, напоминающий машину Атвуда.

См. также

• Плоскость без трения - простая кинематическая модель объекта на пандусе под действием силы тяжести. Страницы, отображающие описания викиданных в качестве запасного варианта.
• Маятник Катера - Реверсивный маятник свободного качания.
• Сферическая корова – юмористическая концепция в научных моделях
• Качающаяся машина Этвуда - вариант машины Этвуда с маятником.

Внешние ссылки

• Трактат о прямолинейном движении и вращении тел; с описанием оригинальных экспериментов по данному предмету, проведенных Джорджем Этвудом, 1764 год. Рисунки представлены на странице 450.
• Отчет профессора Гринслейда о машине Этвуда
• Машина Этвуда Энрике Зелени, Демонстрационный проект Вольфрама