Алгоритм слияния

Алгоритмы слияния — это семейство алгоритмов , которые принимают на вход несколько отсортированных списков и создают на выходе один список, содержащий все элементы входных списков в отсортированном порядке. Эти алгоритмы используются в качестве подпрограмм в различных алгоритмах сортировки , наиболее известный из которых — сортировка слиянием .

Приложение

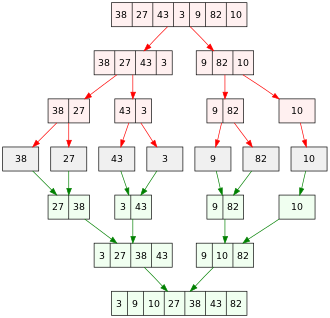
Алгоритм слияния играет решающую роль в алгоритме сортировки слиянием , алгоритме сортировки на основе сравнения . Концептуально алгоритм сортировки слиянием состоит из двух этапов:

Рекурсивно разделите список на подсписки (примерно) одинаковой длины, пока каждый подсписок не будет содержать только один элемент, или, в случае итеративной (снизу вверх) сортировки слиянием, рассматривайте список из n элементов как n подсписков размера 1. список, содержащий один элемент, по определению отсортирован.
Повторно объединяйте подсписки, чтобы создать новый отсортированный подсписок, пока единый список не будет содержать все элементы. Единый список — это отсортированный список.

Алгоритм слияния неоднократно используется в алгоритме сортировки слиянием.

Пример сортировки слиянием приведен на иллюстрации. Он начинается с несортированного массива из 7 целых чисел. Массив разделен на 7 разделов; каждый раздел содержит 1 элемент и отсортирован. Затем отсортированные разделы объединяются для создания более крупных отсортированных разделов, пока не останется один раздел — отсортированный массив.

Объединение двух списков

Объединение двух отсортированных списков в один может осуществляться в линейном времени и линейном или постоянном пространстве (в зависимости от модели доступа к данным). Следующий псевдокод демонстрирует алгоритм, который объединяет входные списки ( списки или массивы ) $A$ и $B$ в новый список $C.$ связанные ^[1]^[2]^: 104 Функция head возвращает первый элемент списка; «Удалить» элемент означает удалить его из списка, обычно путем увеличения указателя или индекса.

algorithm merge(A, B) is    inputs A, B : list    returns list    C := new empty list    while A is not empty and B is not empty do        if head(A) ≤ head(B) then            append head(A) to C            drop the head of A        else            append head(B) to C            drop the head of B    // By now, either A or B is empty. It remains to empty the other input list.    while A is not empty do        append head(A) to C        drop the head of A    while B is not empty do        append head(B) to C        drop the head of B    return C

Когда входные данные представляют собой связанные списки, этот алгоритм можно реализовать для использования только постоянного объема рабочего пространства; указатели в узлах списков можно повторно использовать для бухгалтерского учета и для построения окончательного объединенного списка.

В алгоритме сортировки слиянием эта подпрограмма обычно используется для объединения двух подмассивов. А[ло..мид] , A[mid+1..hi] одного массива А. Это можно сделать, скопировав подмассивы во временный массив, а затем применив описанный выше алгоритм слияния. ^[1] Выделения временного массива можно избежать, но за счет скорости и простоты программирования. Были разработаны различные алгоритмы слияния на месте, ^[3] иногда жертвуя ограничением линейного времени для создания $алгоритма O (n log n)$ ; ^[4] см. раздел «Сортировка слиянием» § Варианты для обсуждения.

K-образное слияние

$k$ -способ слияния обобщает двоичное слияние до произвольного числа $k$ отсортированных входных списков. Приложения $k$ -way слияния возникают в различных алгоритмах сортировки, включая терпеливую сортировку. ^[5] и внешний алгоритм сортировки , который делит входные данные на $k = .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠ 1 / M ⁠ − 1$ блоков, которые помещаются в памяти, сортирует их один за другим, затем объединяет эти блоки. ^[2]^{: 119–120}

Существует несколько решений этой проблемы. Наивное решение — выполнить цикл по $k$ спискам, чтобы каждый раз выбирать минимальный элемент, и повторять этот цикл, пока все списки не станут пустыми:

Входные данные: список из $k$ списков.
Пока любой из списков не пуст:
- Перебирайте списки, чтобы найти список с минимальным первым элементом.
- Выведите минимальный элемент и удалите его из списка.

В худшем случае этот алгоритм выполняет $(k -1)(n - ⁠ k / 2 ⁠)$ сравнения элементов для выполнения своей работы, если всего $n элементов.$ в списках ^[6]Его можно улучшить, сохраняя списки в очереди приоритетов ( min-heap ), ключом которой является их первый элемент:

Создайте минимальную кучу $h$ из $k$ списков, используя первый элемент в качестве ключа.
Пока любой из списков не пуст:
- Пусть $я = find-min(h)$ .
- Выведите первый элемент списка $i$ и удалите его из этого списка.
- Повторно собрать $h$ .

Поиск следующего наименьшего элемента для вывода (find-min) и восстановление порядка кучи теперь можно выполнить за $время O (log k)$ (точнее, $2⌊log k ⌋$ сравнения). ^[6]), и полная проблема может быть решена за $время O (n log k)$ (приблизительно $2 n ⌊log k ⌋$ сравнений). ^[6]^[2]^{: 119–120}

Третий алгоритм решения проблемы — это решение «разделяй и властвуй» , основанное на алгоритме двоичного слияния:

Если $k = 1$ , выведите единственный входной список.
Если $k = 2$ , выполните двоичное слияние.
В противном случае рекурсивно объедините первые $списки ⌊ k /2⌋$ и последние $списки ⌈ k /2⌉$ , а затем объедините их в двоичном виде.

Когда входные списки для этого алгоритма упорядочены по длине, сначала самый короткий, это требует меньше, чем $n ⌈log k ⌉$ сравнений, т. е. меньше половины числа, используемого алгоритмом на основе кучи; на практике он может быть примерно таким же быстрым или медленным, как алгоритм на основе кучи. ^[6]

Параллельное слияние

Параллельная сортировки версия алгоритма двоичного слияния может служить строительным блоком параллельной слиянием . Следующий псевдокод демонстрирует этот алгоритм в параллельном стиле «разделяй и властвуй» (адаптировано из Cormen et al. ^[7]^: 800). Он работает с двумя отсортированными массивами $A$ и $B$ и записывает отсортированный вывод в $C.$ массив Обозначения A[i...j] обозначает часть $A$ от индекса $i$ до $j$ , исключая.

algorithm merge(A[i...j], B[k...ℓ], C[p...q]) is    inputs A, B, C : array           i, j, k, ℓ, p, q : indices    let m = j - i,        n = ℓ - k    if m < n then        swap A and B  // ensure that A is the larger array: i, j still belong to A; k, ℓ to B        swap m and n    if m ≤ 0 then        return  // base case, nothing to merge    let r = ⌊(i + j)/2⌋    let s = binary-search(A[r], B[k...ℓ])    let t = p + (r - i) + (s - k)    C[t] = A[r]    in parallel do        merge(A[i...r], B[k...s], C[p...t])        merge(A[r+1...j], B[s...ℓ], C[t+1...q])

Алгоритм работает путем разделения $A$ или $B$ (в зависимости от того, что больше) на (почти) равные половины. Затем он разбивает другой массив на часть со значениями, меньшими, чем середина первого, и часть с большими или равными значениями. ( Подпрограмма двоичного поиска возвращает индекс в $B$ , где $A [r]$ было бы $, если бы оно было в B$ ; что это всегда число между $k$ и $ℓ$ объединяется .) Наконец, каждая пара половин рекурсивно , и поскольку рекурсивные вызовы независимы друг от друга, их можно выполнять параллельно. На практике было показано, что гибридный подход, при котором последовательный алгоритм используется для базового случая рекурсии, хорошо работает. ^[8]

Работа , выполняемая алгоритмом для двух массивов, содержащих в общей сложности $n$ элементов, т. е. время работы его последовательной версии, равна $O (n)$ . Это оптимально, поскольку $n$ необходимо скопировать $в C$ элементов . Чтобы вычислить диапазон алгоритма, необходимо вывести Рекуррентное соотношение . Поскольку два рекурсивных вызова слияния выполняются параллельно, необходимо учитывать только более затратный из двух вызовов. В худшем случае максимальное количество элементов в одном из рекурсивных вызовов не превышает ${\textstyle {\frac {3}{4}}n}$ поскольку массив с большим количеством элементов идеально разбивается пополам. Добавление $\Theta \left(\log(n)\right)$ стоимости двоичного поиска, мы получаем эту повторяемость как верхнюю границу:

$T_{\infty }^{\text{merge}}(n)=T_{\infty }^{\text{merge}}\left({\frac {3}{4}}n\right)+\Theta \left(\log(n)\right)$

Решение $T_{\infty }^{\text{merge}}(n)=\Theta \left(\log(n)^{2}\right)$ , то есть столько времени требуется на идеальной машине с неограниченным количеством процессоров. ^[7]^{: 801–802}

Примечание. Процедура нестабильна : если равные элементы разделены разделением $A$ и $B$ , они будут чередоваться в $C$ ; также замена $A$ и $B$ разрушит порядок, если одинаковые элементы распределены между обоими входными массивами. В результате при использовании этого алгоритма для сортировки сортировка становится нестабильной.

Параллельное объединение двух списков

Существуют также алгоритмы, которые обеспечивают параллелизм в одном экземпляре слияния двух отсортированных списков. Их можно использовать в программируемых вентильных матрицах ( FPGA ), специализированных схемах сортировки, а также в современных процессорах с инструкциями с одной командой и несколькими данными ( SIMD ).

Существующие параллельные алгоритмы основаны на модификациях части слияния либо битонического сортировщика , либо сортировки слиянием нечетно-четных . ^[9] В 2018 году Сайто М. и др. представил ММС ^[10] для FPGA, которые были сосредоточены на удалении пути передачи данных с многоцикловой обратной связью, который препятствовал эффективной конвейерной передаче данных в аппаратном обеспечении. Также в 2018 г. Папафилиппу П. и др. представил FLiMS ^[9] что улучшило использование оборудования и производительность, требуя только $\log _{2}(P)+1$ этапы конвейера $блоков сравнения и замены P/2$ для объединения с параллелизмом $элементов P$ за цикл FPGA.

Языковая поддержка

Некоторые языки программирования предоставляют встроенную или библиотечную поддержку объединения отсортированных коллекций .

С++

В C++ есть стандартной библиотеке шаблонов функция std::merge , который объединяет два отсортированных диапазона итераторов , и std::inplace_merge , который объединяет два последовательных отсортированных диапазона на месте . Кроме того, Класс std::list (связанный список) имеет свой собственный merge метод, который объединяет другой список в себя. Тип объединяемых элементов должен поддерживать формат «меньше чем» ( < ) или ему должен быть предоставлен специальный компаратор.

C++17 допускает различные политики выполнения, а именно последовательную, параллельную и параллельно-неупорядоченную. ^[11]

Питон

имеет Стандартная библиотека Python (начиная с версии 2.6) также функция слияния в heapq , который принимает несколько отсортированных итераций и объединяет их в один итератор. ^[12]

См. также

Ссылки

^ Jump up to: ^а ^б Скиена, Стивен (2010). Руководство по разработке алгоритмов (2-е изд.). Springer Science+Business Media . п. 123. ИСБН 978-1-849-96720-4 .
^ Jump up to: ^а ^б ^с Курт Мельхорн ; Питер Сандерс (2008). Алгоритмы и структуры данных: базовый набор инструментов . Спрингер. ISBN 978-3-540-77978-0 .
^ Можжевельник, Юрки; Пасанен, Томи; Теухола, Юкка (1996). «Практическая сортировка слиянием на месте». Нордик Дж. Компьютерные технологии . 3 (1): 27–40. CiteSeerX 10.1.1.22.8523 .
^ Ким, Пок-Сон; Куцнер, Арне (2004). Стабильное объединение минимального объема памяти посредством симметричных сравнений . Европейский симп. Алгоритмы. Конспекты лекций по информатике. Том. 3221. стр. 714–723. CiteSeerX 10.1.1.102.4612 . дои : 10.1007/978-3-540-30140-0_63 . ISBN 978-3-540-23025-0 .
^ Чандрамули, Бадриш; Гольдштейн, Джонатан (2014). Терпение — добродетель: новый взгляд на слияние и сортировку на современных процессорах . СИГМОД/ПОДС.
^ Jump up to: ^а ^б ^с ^д Грин, Уильям А. (1993). k-образное слияние и k-арная сортировка (PDF) . Учеб. 31-я ежегодная Юго-восточная конференция ACM. стр. 127–135.
^ Jump up to: ^а ^б Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л .; Стоун, Клиффорд (2009) [1990]. Введение в алгоритмы (3-е изд.). MIT Press и McGraw-Hill. ISBN 0-262-03384-4 .
^ Виктор Юрьевич Дуваненко (2011), «Параллельное слияние» , Dr. Журнал Добба
^ Jump up to: ^а ^б Папафилиппу, Филиппос; Люк, Уэйн; Брукс, Крис (2022). «FLiMS: быстрое и легкое двустороннее слияние для сортировки». Транзакции IEEE на компьютерах : 1–12. дои : 10.1109/TC.2022.3146509 . hdl : 10044/1/95271 . S2CID 245669103 .
^ Сайто, Макото; Эльсайед, Эльсайед А.; Чу, Тим Ван; Машимо, Сусуму; Кисе, Кенджи (апрель 2018 г.). «Высокопроизводительный и экономичный аппаратный сортировщик слиянием без обратной связи». 26-й ежегодный международный симпозиум IEEE по программируемым пользовательским вычислительным машинам (FCCM) , 2018 г. стр. 197–204. дои : 10.1109/FCCM.2018.00038 . ISBN 978-1-5386-5522-1 . S2CID 52195866 .
^ «станд: слияние» . cppreference.com. 08.01.2018 . Проверено 28 апреля 2018 г.
^ «heapq — Алгоритм очереди кучи — документация Python 3.10.1» .

Дальнейшее чтение

Дональд Кнут . Искусство компьютерного программирования , Том 3: Сортировка и поиск , Третье издание. Аддисон-Уэсли, 1997. ISBN 0-201-89685-0 . Страницы 158–160 раздела 5.2.4: Сортировка путем слияния. Раздел 5.3.2: Слияние минимального сравнения, стр. 197–207.

Внешние ссылки

Высокопроизводительная реализация параллельного и последовательного слияния на C# с исходным кодом в GitHub и в C++ GitHub

[skiena-1] Jump up to: ^а ^б Скиена, Стивен (2010). Руководство по разработке алгоритмов (2-е изд.). Springer Science+Business Media . п. 123. ИСБН 978-1-849-96720-4 .

[toolbox-2] Jump up to: ^а ^б ^с Курт Мельхорн ; Питер Сандерс (2008). Алгоритмы и структуры данных: базовый набор инструментов . Спрингер. ISBN 978-3-540-77978-0 .

[3] Можжевельник, Юрки; Пасанен, Томи; Теухола, Юкка (1996). «Практическая сортировка слиянием на месте». Нордик Дж. Компьютерные технологии . 3 (1): 27–40. CiteSeerX 10.1.1.22.8523 .

[4] Ким, Пок-Сон; Куцнер, Арне (2004). Стабильное объединение минимального объема памяти посредством симметричных сравнений . Европейский симп. Алгоритмы. Конспекты лекций по информатике. Том. 3221. стр. 714–723. CiteSeerX 10.1.1.102.4612 . дои : 10.1007/978-3-540-30140-0_63 . ISBN 978-3-540-23025-0 .

[Chandramouli-5] Чандрамули, Бадриш; Гольдштейн, Джонатан (2014). Терпение — добродетель: новый взгляд на слияние и сортировку на современных процессорах . СИГМОД/ПОДС.

[greene-6] Jump up to: ^а ^б ^с ^д Грин, Уильям А. (1993). k-образное слияние и k-арная сортировка (PDF) . Учеб. 31-я ежегодная Юго-восточная конференция ACM. стр. 127–135.

[clrs-7] Jump up to: ^а ^б Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л .; Стоун, Клиффорд (2009) [1990]. Введение в алгоритмы (3-е изд.). MIT Press и McGraw-Hill. ISBN 0-262-03384-4 .

[vjd-8] Виктор Юрьевич Дуваненко (2011), «Параллельное слияние» , Dr. Журнал Добба

[flimsj-9] Jump up to: ^а ^б Папафилиппу, Филиппос; Люк, Уэйн; Брукс, Крис (2022). «FLiMS: быстрое и легкое двустороннее слияние для сортировки». Транзакции IEEE на компьютерах : 1–12. дои : 10.1109/TC.2022.3146509 . hdl : 10044/1/95271 . S2CID 245669103 .

[10] Сайто, Макото; Эльсайед, Эльсайед А.; Чу, Тим Ван; Машимо, Сусуму; Кисе, Кенджи (апрель 2018 г.). «Высокопроизводительный и экономичный аппаратный сортировщик слиянием без обратной связи». 26-й ежегодный международный симпозиум IEEE по программируемым пользовательским вычислительным машинам (FCCM) , 2018 г. стр. 197–204. дои : 10.1109/FCCM.2018.00038 . ISBN 978-1-5386-5522-1 . S2CID 52195866 .

[11] «станд: слияние» . cppreference.com. 08.01.2018 . Проверено 28 апреля 2018 г.

[12] «heapq — Алгоритм очереди кучи — документация Python 3.10.1» .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

v т и Алгоритмы сортировки
Теория	Теория сложности вычислений Обозначение большого О Общий заказ Списки Размещение Стабильность Сортировка сравнения Адаптивная сортировка Сортировочная сеть Целочисленная сортировка X + Y сортировка Трансдихотомическая модель Квантовая сортировка
Обмен сортами	Пузырьковая сортировка Сорт коктейльного шейкера Нечетно-четный сорт Гребенчатая сортировка Гном сортирует Пропорциональное расширение сортировки Быстрая сортировка
Сортировки выбора	Сортировка выбором пирамидальная сортировка Гладкая сортировка Декартова сортировка дерева Сортировка турниров Циклическая сортировка Слабая пирамидальная сортировка
Сортировки вставками	Сортировка вставкой Шеллсорт Сплейсорт Сортировка дерева Сортировка библиотеки Сортировка терпения
Объединить сортировки	Идет судьба Каскадная сортировка слиянием Осциллирующая сортировка слиянием Многофазная сортировка слиянием
Виды распределения	сорт американского флага Сортировка бисера Сортировка ведром Пакетная сортировка Подсчет сортировки Интерполяционная сортировка Сортировка по ячейкам Сортировка проксмап Поразрядная сортировка Флэш-сортировка
Параллельные сортировки	Битонический сортировщик Батчерная сортировка слиянием нечет-чет Попарная сортировочная сеть Выборочная сортировка
Гибридные сорта	Блокировать сортировку слиянием Сорт Киркпатрика – Райша Тимсорт Интросорт Спред-сортировка Сортировка слиянием-вставкой
Другой	Топологическая сортировка Предтопологический порядок Сортировка блинов Спагетти сорт
Непрактичные сорта	марионетка сортировка медленная сортировка Богосорт