Теория Брахмагупты

В геометрии вписанный теорема Брахмагупты утверждает, что если четырехугольник ортодиагонален . (то есть имеет перпендикулярные диагонали ), то перпендикуляр к стороне из точки пересечения диагоналей всегда делит противоположную сторону пополам [1] Назван в честь индийского математика Брахмагупты (598-668). [2]
Более конкретно, пусть A , B , C и D — четыре точки на окружности, такие, что прямые AC и BD перпендикулярны. пересечение AC и BD через M. Обозначим Опустите перпендикуляр из М прямую ВС , назвав пересечение Е. на Пусть F — пересечение прямой EM и ребра AD . Тогда теорема утверждает, что F — это середина AD .
Доказательство [ править ]
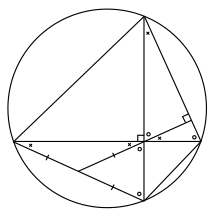
Нам нужно доказать, что AF = FD . Мы докажем, что и AF , и FD на самом деле равны FM .
Чтобы доказать, что AF = FM , сначала заметим, что углы FAM и CBM равны, поскольку они являются вписанными углами , пересекающими одну и ту же дугу окружности (CD). углы CBM и CME дополняют Более того , угол BCM (т.е. их сумма составляет 90°) и поэтому равны. Наконец, углы CME и FMA одинаковы. Следовательно, AFM — равнобедренный треугольник , следовательно, стороны AF и FM равны.
Доказательство того, что FD = FM, проходит аналогично: углы FDM , BCM , BME и DMF равны, поэтому DFM — равнобедренный треугольник, поэтому FD = FM . Отсюда следует, что AF = FD , как утверждает теорема.
См. также [ править ]
- Формула Брахмагупты для площади вписанного четырехугольника
Ссылки [ править ]
- ^ Майкл Джон Брэдли (2006). Рождение математики: от древности до 1300 года . Издательство Информационная база издательства. ISBN 0816054231 . Стр. 70, 85.
- ^ Коксетер, HSM ; Грейцер, С.Л.: Возвращение к геометрии . Вашингтон, округ Колумбия: Математика. доц. Амер., с. 59, 1967 г.

