Минипоплавок

В вычислительной технике мини -числа с плавающей запятой представляют собой значения с плавающей запятой, представленные очень небольшим количеством битов . Как и следовало ожидать, они не очень подходят для численных расчетов общего назначения. Они используются для специальных целей, например, для

Компьютерная графика, где итерации небольшие, а точность имеет эстетический эффект. ^[1]
Машинное обучение , которое может быть относительно нечувствительным к числовой точности. bfloat16 и fp8 — распространенные форматы. ^[2]

Кроме того, они часто используются в качестве педагогического инструмента на курсах информатики для демонстрации свойств и структур арифметики с плавающей запятой и IEEE 754 чисел .

Мини-плавающие числа с 16 битами представляют собой числа половинной точности (в отличие от одинарной и двойной точности ). Существуют также мини-поплавки с 8 битами или даже меньше. ^[2]

Минипоплавки могут быть спроектированы в соответствии с принципами стандарта IEEE 754 . В этом случае они должны подчиняться (не прописанным явно) правилам границы между субнормальными и нормальными числами и должны иметь специальные шаблоны для бесконечности и NaN . Нормализованные числа хранятся со смещенной экспонентой . Новая версия стандарта IEEE 754-2008 имеет 16-битные двоичные числа с плавающей запятой .

Обозначения

Мини-флоат обычно описывается с помощью кортежа из четырех чисел ( S , E , M , B ):

S — длина знакового поля. Обычно это либо 0, либо 1.
E — длина поля показателя.
M — длина поля мантиссы (значащего значения).
B — смещение показателя .

Следовательно, формат minifloat, обозначаемый ( S , E , M , B ), имеет $длину S + E + M$ бит. Нотация ( S , E , M , B ) может быть преобразована в формат ( B , P , L , U ) как $(2, M + 1, B + 1, 2 С - B)$ (с использованием показателей IEEE).

Пример 8-битного числа с плавающей запятой (1.4.3)

Схема примера 8-битного мини-плавающего числа (1.4.3)
знак	показатель степени				значимое значение
0	0	0	0	0	0	0	0

Здесь показано мини-число с плавающей запятой размером 1 байт (8 бит) с 1 знаковым битом, 4 битами экспоненты и 3 битами мантиссы (короче говоря, мини-плавающее число 1.4.3). определяется Смещение экспоненты как 7, чтобы центрировать значения вокруг 1, чтобы соответствовать другим числам с плавающей запятой IEEE 754. ^[3]^[4] поэтому (для большинства значений) фактический множитель для показателя $x$ равен $2 х -7$ . Все принципы IEEE 754 должны быть действительными. ^[5]

Числа в другой базе помечаются как ... _base , например, 101 ₂ = 5. Битовые комбинации имеют пробелы для визуализации своих частей.

Представление нуля

Ноль представлен как нулевой показатель степени с нулевой мантиссой. Нулевой показатель степени означает, что ноль — это субнормальное число с ведущим «0». префикс, а с нулевой мантиссой все биты после десятичной точки равны нулю, то есть это значение интерпретируется как $0.000_{2}\times 2^{-6}=0$ . Числа с плавающей запятой используют ноль со знаком , поэтому $-0$ также имеется и равен положительному $0$ .

0 0000 000 = 0
1 0000 000 = −0

Субнормальные числа

Мантисса расширяется с помощью «0». и значение показателя степени рассматривается как на 1 больше, чем наименее нормализованное число:

0 0000 001 = 0.001₂ × 2^{1 - 7} = 0.125 × 2^-6 = 0.001953125 (least subnormal number)
...
0 0000 111 = 0.111₂ × 2^{1 - 7} = 0.875 × 2^-6 = 0.013671875 (greatest subnormal number)

Нормализованные числа

Мантисса расширяется с помощью «1»:

0 0001 000 = 1.000₂ × 2^{1 - 7} = 1 × 2^-6 = 0.015625 (least normalized number)
0 0001 001 = 1.001₂ × 2^{1 - 7} = 1.125 × 2^-6 = 0.017578125
...
0 0111 000 = 1.000₂ × 2^{7 - 7} = 1 × 2⁰ = 1
0 0111 001 = 1.001₂ × 2^{7 - 7} = 1.125 × 2⁰ = 1.125 (least value above 1)
...
0 1110 000 = 1.000₂ × 2^{14 - 7} =  1.000 × 2⁷ =  128
0 1110 001 = 1.001₂ × 2^{14 - 7} =  1.125 × 2⁷ =  144
...
0 1110 110 = 1.110₂ × 2^{14 - 7} =  1.750 × 2⁷ = 224
0 1110 111 = 1.111₂ × 2^{14 - 7} =  1.875 × 2⁷ = 240 (greatest normalized number)

Бесконечность

Значения бесконечности имеют наивысший показатель степени, а мантисса равна нулю. Знаковый бит может быть как положительным, так и отрицательным.

0 1111 000 = +infinity
1 1111 000 = −infinity

Не число

Значения NaN имеют наивысший показатель степени с ненулевым значением мантиссы. Число с плавающей запятой с 1-битным знаком и 3-битной мантиссой имеет $2\times (2^{3}-1)=14$ значения NaN.

s 1111 mmm = NaN (if mmm ≠ 000)

Таблица значений

Это диаграмма всех возможных значений для этого примера 8-битного числа с плавающей запятой.

	… 000	… 001	… 010	… 011	… 100	… 101	… 110	… 111
0 0000 …	0	0.001953125	0.00390625	0.005859375	0.0078125	0.009765625	0.01171875	0.013671875
0 0001 …	0.015625	0.017578125	0.01953125	0.021484375	0.0234375	0.025390625	0.02734375	0.029296875
0 0010 …	0.03125	0.03515625	0.0390625	0.04296875	0.046875	0.05078125	0.0546875	0.05859375
0 0011 …	0.0625	0.0703125	0.078125	0.0859375	0.09375	0.1015625	0.109375	0.1171875
0 0100 …	0.125	0.140625	0.15625	0.171875	0.1875	0.203125	0.21875	0.234375
0 0101 …	0.25	0.28125	0.3125	0.34375	0.375	0.40625	0.4375	0.46875
0 0110 …	0.5	0.5625	0.625	0.6875	0.75	0.8125	0.875	0.9375
0 0111 …	1	1.125	1.25	1.375	1.5	1.625	1.75	1.875
0 1000 …	2	2.25	2.5	2.75	3	3.25	3.5	3.75
0 1001 …	4	4.5	5	5.5	6	6.5	7	7.5
0 1010 …	8	9	10	11	12	13	14	15
0 1011 …	16	18	20	22	24	26	28	30
0 1100 …	32	36	40	44	48	52	56	60
0 1101 …	64	72	80	88	96	104	112	120
0 1110 …	128	144	160	176	192	208	224	240
0 1111 …	Инф	НЭН	НЭН	НЭН	НЭН	НЭН	НЭН	НЭН
1 0000 …	−0	−0.001953125	−0.00390625	−0.005859375	−0.0078125	−0.009765625	−0.01171875	−0.013671875
1 0001 …	−0.015625	−0.017578125	−0.01953125	−0.021484375	−0.0234375	−0.025390625	−0.02734375	−0.029296875
1 0010 …	−0.03125	−0.03515625	−0.0390625	−0.04296875	−0.046875	−0.05078125	−0.0546875	−0.05859375
1 0011 …	−0.0625	−0.0703125	−0.078125	−0.0859375	−0.09375	−0.1015625	−0.109375	−0.1171875
1 0100 …	−0.125	−0.140625	−0.15625	−0.171875	−0.1875	−0.203125	−0.21875	−0.234375
1 0101 …	−0.25	−0.28125	−0.3125	−0.34375	−0.375	−0.40625	−0.4375	−0.46875
1 0110 …	−0.5	−0.5625	−0.625	−0.6875	−0.75	−0.8125	−0.875	−0.9375
1 0111 …	−1	−1.125	−1.25	−1.375	−1.5	−1.625	−1.75	−1.875
1 1000 …	−2	−2.25	−2.5	−2.75	−3	−3.25	−3.5	−3.75
1 1001 …	−4	−4.5	−5	−5.5	−6	−6.5	−7	−7.5
1 1010 …	−8	−9	−10	−11	−12	−13	−14	−15
1 1011 …	−16	−18	−20	−22	−24	−26	−28	−30
1 1100 …	−32	−36	−40	−44	−48	−52	−56	−60
1 1101 …	−64	−72	−80	−88	−96	−104	−112	−120
1 1110 …	−128	−144	−160	−176	−192	−208	−224	−240
1 1111 …	−Инф	НЭН	НЭН	НЭН	НЭН	НЭН	НЭН	НЭН

Существует только 242 различных значения, отличных от NaN (если +0 и -0 считаются разными), поскольку 14 битовых комбинаций представляют NaN.

Альтернативные значения смещения

При этих небольших размерах могут быть интересны другие значения смещения, например, смещение -2 приведет к тому, что числа 0–16 будут иметь то же битовое представление, что и целые числа 0–16, с потерей, что никакие нецелые значения не могут быть представлены.

0 0000 000 = 0.000₂ × 2^{1 - (-2)} = 0.0 × 2³ = 0 (subnormal number)
0 0000 001 = 0.001₂ × 2^{1 - (-2)} = 0.125 × 2³ = 1 (subnormal number)
0 0000 111 = 0.111₂ × 2^{1 - (-2)} = 0.875 × 2³ = 7 (subnormal number)
0 0001 000 = 1.000₂ × 2^{1 - (-2)} = 1.000 × 2³ = 8 (normalized number)
0 0001 111 = 1.111₂ × 2^{1 - (-2)} = 1.875 × 2³ = 15 (normalized number)
0 0010 000 = 1.000₂ × 2^{2 - (-2)} = 1.000 × 2⁴ = 16 (normalized number)

Различные распределения битов

Выше описан пример 8-битного числа с плавающей запятой с 1 битом знака, 4 битами экспоненты и 3 битами мантиссы, что является хорошим балансом. Однако возможно любое распределение битов. Формат может выбрать предоставление большего количества битов экспоненте, если им нужен больший динамический диапазон с меньшей точностью, или предоставление большего количества битов мантиссе, если им нужна большая точность с меньшим динамическим диапазоном. В крайнем случае, можно отдать все биты экспоненте или все биты, кроме одного, мантиссе, оставив экспоненте только один бит. Экспоненте должен быть присвоен хотя бы один бит, иначе она больше не имеет смысла как число с плавающей запятой, а просто становится числом со знаком .

Вот таблица всех возможных значений для различных 8-битных чисел с плавающей запятой с 1 битом знака, 3 битами экспоненты и 4 битами мантиссы. Наличие на 1 бит значащего числа больше, чем битов экспоненты, гарантирует, что точность останется не ниже 0,5 во всем диапазоне. ^[6]

	… 0000	… 0001	… 0010	… 0011	… 0100	… 0101	… 0110	… 0111	… 1000	… 1001	… 1010	… 1011	… 1100	… 1101	… 1110	… 1111
0 000 …	0	0.015625	0.03125	0.046875	0.0625	0.078125	0.09375	0.109375	0.125	0.140625	0.15625	0.171875	0.1875	0.203125	0.21875	0.234375
0 001 …	0.25	0.265625	0.28125	0.296875	0.3125	0.328125	0.34375	0.359375	0.375	0.390625	0.40625	0.421875	0.4375	0.453125	0.46875	0.484375
0 010 …	0.5	0.53125	0.5625	0.59375	0.625	0.65625	0.6875	0.71875	0.75	0.78125	0.8125	0.84375	0.875	0.90625	0.9375	0.96875
0 011 …	1	1.0625	1.125	1.1875	1.25	1.3125	1.375	1.4375	1.5	1.5625	1.625	1.6875	1.75	1.8125	1.875	1.9375
0 100 …	2	2.125	2.25	2.375	2.5	2.625	2.75	2.875	3	3.125	3.25	3.375	3.5	3.625	3.75	3.875
0 101 …	4	4.25	4.5	4.75	5	5.25	5.5	5.75	6	6.25	6.5	6.75	7	7.25	7.5	7.75
0 110 …	8	8.5	9	9.5	10	10.5	11	11.5	12	12.5	13	13.5	14	14.5	15	15.5
0 111 …	Инф	НЭН	НЭН	НЭН	НЭН	НЭН	НЭН	НЭН	НЭН	НЭН	НЭН	НЭН	НЭН	НЭН	НЭН	НЭН
1 000 …	−0	−0.015625	−0.03125	−0.046875	−0.0625	−0.078125	−0.09375	−0.109375	−0.125	−0.140625	−0.15625	−0.171875	−0.1875	−0.203125	−0.21875	−0.234375
1 001 …	−0.25	−0.265625	−0.28125	−0.296875	−0.3125	−0.328125	−0.34375	−0.359375	−0.375	−0.390625	−0.40625	−0.421875	−0.4375	−0.453125	−0.46875	−0.484375
1 010 …	−0.5	−0.53125	−0.5625	−0.59375	−0.625	−0.65625	−0.6875	−0.71875	−0.75	−0.78125	−0.8125	−0.84375	−0.875	−0.90625	−0.9375	−0.96875
1 011 …	−1	−1.0625	−1.125	−1.1875	−1.25	−1.3125	−1.375	−1.4375	−1.5	−1.5625	−1.625	−1.6875	−1.75	−1.8125	−1.875	−1.9375
1 100 …	−2	−2.125	−2.25	−2.375	−2.5	−2.625	−2.75	−2.875	−3	−3.125	−3.25	−3.375	−3.5	−3.625	−3.75	−3.875
1 101 …	−4	−4.25	−4.5	−4.75	−5	−5.25	−5.5	−5.75	−6	−6.25	−6.5	−6.75	−7	−7.25	−7.5	−7.75
1 110 …	−8	−8.5	−9	−9.5	−10	−10.5	−11	−11.5	−12	−12.5	−13	−13.5	−14	−14.5	−15	−15.5
1 111 …	−Инф	НЭН	НЭН	НЭН	НЭН	НЭН	НЭН	НЭН	НЭН	НЭН	НЭН	НЭН	НЭН	НЭН	НЭН	НЭН

Таблицы, подобные приведенной выше, могут быть созданы для любой комбинации значений SEMB (знак, показатель степени, мантисса/значащее число и смещение) с использованием сценария на Python или GDScript .

Арифметика

Добавление

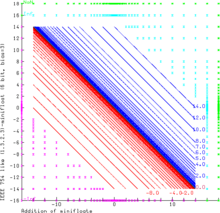
На графике показано добавление еще меньших (1.3.2.3)-минипоплавков с 6 битами. Эта система с плавающей запятой точно соответствует правилам IEEE 754. NaN в качестве операнда всегда дает результат NaN. Inf − Inf и (−Inf) + Inf также дают NaN (зеленая область). Inf можно увеличивать и уменьшать на конечные значения без изменений. Суммы с конечными операндами могут давать бесконечный результат (т. е. 14,0 + 3,0 = +Inf в результате — голубая область, −Inf — пурпурная область). Диапазон конечных операндов заполнен кривыми x + y = c , где c всегда является одним из представимых значений с плавающей запятой (синий и красный для положительных и отрицательных результатов соответственно).

Вычитание, умножение и деление

Остальные арифметические операции можно проиллюстрировать аналогичным образом:

Вычитание
Умножение
Разделение

Другие размеры

Графические процессоры Radeon R300 и R420 использовали формат с плавающей запятой «fp24» с 7 битами экспоненты и 16 битами (+1 неявная) мантиссы. ^[7] «Полная точность» в Direct3D 9.0 — это собственный 24-битный формат с плавающей запятой. Microsoft D3D9 (Shader Model 2.0) Графический API изначально поддерживал как FP24 (как в чипе ATI R300), так и FP32 (как в чипе NV30 от Nvidia) как «Полная точность», а также FP16 как «Частичную точность» для вычислений вершинных и пиксельных шейдеров. выполняется графическим оборудованием.

Khronos определяет 10-битные и 11-битные форматы чисел с плавающей запятой для использования с Vulkan. Оба формата не имеют знакового бита и имеют 5-битный показатель степени. 10-битный формат имеет 5-битную мантиссу, а 11-битный формат — 6-битную мантиссу. ^[8]^[9]

Рабочая группа IEEE SA P3109 в настоящее время работает над стандартом для 8-битных чисел с плавающей запятой, оптимизированным для машинного обучения. Текущий проект определяет не один формат, а семейство из 7 различных форматов под названием «binary8pP», где «P» — число от 1 до 7. Эти числа с плавающей запятой разработаны так, чтобы быть компактными и эффективными, но не следуют одной и той же семантике. как и другие числа с плавающей точкой IEEE, и в них отсутствуют такие функции, как отрицательный ноль и множественные значения NaN. Бесконечность определяется как показатель степени и мантисса, имеющие все единицы, вместо других чисел с плавающей запятой IEEE, где показатель степени представляет собой все единицы, а мантисса - все нули. ^[10]

4 бита и меньше

Наименьший возможный размер с плавающей запятой, соответствующий всем принципам IEEE, включая нормализованные числа, субнормальные числа, ноль со знаком, бесконечность со знаком и несколько значений NaN, представляет собой 4-битное число с плавающей запятой с 1-битным знаком, 2-битной экспонентой и 1-битным числом. мантисса. ^[11] В таблице ниже столбцы имеют разные значения битов знака и мантиссы, а строки — разные значения битов экспоненты.

	0 … 0	0 … 1	1 … 0	1 … 1
… 00 …	0	0.5	−0	−0.5
… 01 …	1	1.5	−1	−1.5
… 10 …	2	3	−2	−3
… 11 …	Инф	НЭН	−Инф	НЭН

Если нормализованные числа не требуются, размер можно уменьшить до 3 бит, уменьшив показатель степени до 1.

	0 … 0	0 … 1	1 … 0	1 … 1
… 0 …	0	1	−0	−1
… 1 …	Инф	НЭН	−Инф	НЭН

В ситуациях, когда знаковый бит можно исключить, каждый из приведенных выше примеров можно уменьшить еще на 1 бит, сохранив только левую половину приведенных выше таблиц. 2-битное число с плавающей запятой с 1-битной экспонентой и 1-битной мантиссой будет иметь только значения 0, 1, Inf, NaN.

Если мантисса может быть 0-битной, 1-битный формат с плавающей запятой будет иметь 1-битную экспоненту, и единственными двумя значениями будут 0 и Inf. Экспонента должна быть не менее 1 бита, иначе она больше не имеет смысла как число с плавающей запятой (это будет просто число со знаком ).

4-битные числа с плавающей запятой — без четырех специальных значений IEEE — нашли применение для ускорения больших языковых моделей . ^[12]

Во встроенных устройствах

Минипоплавки также часто используются во встроенных устройствах. ^{[ нужна ссылка ]} особенно на микроконтроллерах , где операции с плавающей запятой необходимо эмулировать программно. Чтобы ускорить вычисления, мантисса обычно занимает ровно половину битов, поэтому граница регистра автоматически обращается к частям без смещения.

См. также

Ссылки

^ Мочерино, Лука; Калимера, Андреа (24 ноября 2021 г.). «AxP: Конвейер совместного проектирования HW-SW для энергоэффективных аппроксимированных сверточных сетей посредством ассоциативного сопоставления» . Прикладные науки . 11 (23): 11164. doi : 10.3390/app112311164 .
↑ Перейти обратно: Перейти обратно: ^а ^б https://developer.nvidia.com/blog/nvidia-arm-and-intel-publish-fp8-specification-for-standardization-as-an-interchange-format-for-ai/ (совместное объявление Intel, NVIDIA, Рука); https://arxiv.org/abs/2209.05433 (препринт, совместно написанный исследователями из трех вышеупомянутых компаний)
^ Половинная точность IEEE имеет 5 битов экспоненты со смещением 15 ( $2^{5-1}-1=15$ ), IEEE одинарной точности имеет 8 бит экспоненты со смещением 127 ( $2^{8-1}-1=127$ ), IEEE двойной точности имеет 11 бит экспоненты со смещением 1023 ( $2^{11-1}-1=1023$ ), а IEEE четверной точности имеет 15 бит экспоненты со смещением 16383 ( $2^{15-1}-1=16383$ ). см. в статье «Смещение экспоненты» . Более подробную информацию
^ О'Халларон, Дэвид Р.; Брайант, Рэндал Э. (2010). Компьютерные системы: взгляд программиста (2-е изд.). Бостон, Массачусетс, США: Прентис Холл . ISBN 978-0-13-610804-7 .
^ Берч, Карл. «Представление с плавающей запятой» . Хендрикс Колледж . Проверено 29 августа 2023 г.
^ https://people.cs.umass.edu/~verts/cmpsci145/8-Bit_Floating_Point.pdf
^ Бак, Ян (13 марта 2005 г.), «Глава 32. Окунуться в вычисления на графических процессорах» , в Фарр, Мэтт (редактор), GPU Gems , ISBN 0-321-33559-7 , получено 5 апреля 2018 г.
^ Гаррард, Эндрю. «10.3. Беззнаковые 10-битные числа с плавающей запятой» . Спецификация формата данных Khronos v1.2, ред. 1 . Группа компаний «Хронос» . Проверено 10 августа 2023 г.
^ Гаррард, Эндрю. «10.2. Беззнаковые 11-битные числа с плавающей запятой» . Спецификация формата данных Khronos v1.2, ред. 1 . Группа компаний «Хронос» . Проверено 10 августа 2023 г.
^ «Промежуточный отчет рабочей группы IEEE P3109 по 8-битным двоичным форматам с плавающей запятой» (PDF) . Гитхаб . Рабочая группа IEEE P3109. Архивировано из оригинала (PDF) 21 февраля 2024 года . Проверено 7 мая 2024 г.
^ Шейнифелт, доктор Тед. «Гизмо доктора Шейнифельта, создающее плавающую точку» . Доктор Тед Шейнифелт . Проверено 29 августа 2023 г.
^ https://www.intel.com/content/www/us/en/developer/articles/technical/accelerating-language-model-inference-on-your-pc.html .

Мунафо, Роберт (15 мая 2016 г.). «Обзор форматов с плавающей запятой» . Проверено 8 августа 2016 г.

Внешние ссылки

Полуплавающий пиксель OpenGL

[1] Мочерино, Лука; Калимера, Андреа (24 ноября 2021 г.). «AxP: Конвейер совместного проектирования HW-SW для энергоэффективных аппроксимированных сверточных сетей посредством ассоциативного сопоставления» . Прикладные науки . 11 (23): 11164. doi : 10.3390/app112311164 .

[fp8-ml-2] Перейти обратно: Перейти обратно: ^а ^б https://developer.nvidia.com/blog/nvidia-arm-and-intel-publish-fp8-specification-for-standardization-as-an-interchange-format-for-ai/ (совместное объявление Intel, NVIDIA, Рука); https://arxiv.org/abs/2209.05433 (препринт, совместно написанный исследователями из трех вышеупомянутых компаний)

[3] Половинная точность IEEE имеет 5 битов экспоненты со смещением 15 ( $2^{5-1}-1=15$ ), IEEE одинарной точности имеет 8 бит экспоненты со смещением 127 ( $2^{8-1}-1=127$ ), IEEE двойной точности имеет 11 бит экспоненты со смещением 1023 ( $2^{11-1}-1=1023$ ), а IEEE четверной точности имеет 15 бит экспоненты со смещением 16383 ( $2^{15-1}-1=16383$ ). см. в статье «Смещение экспоненты» . Более подробную информацию

[Bryant_2010-4] О'Халларон, Дэвид Р.; Брайант, Рэндал Э. (2010). Компьютерные системы: взгляд программиста (2-е изд.). Бостон, Массачусетс, США: Прентис Холл . ISBN 978-0-13-610804-7 .

[5] Берч, Карл. «Представление с плавающей запятой» . Хендрикс Колледж . Проверено 29 августа 2023 г.

[6] ttps://people.cs.umass.edu/~verts/cmpsci145/8-Bit_Floating_Point.pdf

[7] Бак, Ян (13 марта 2005 г.), «Глава 32. Окунуться в вычисления на графических процессорах» , в Фарр, Мэтт (редактор), GPU Gems , ISBN 0-321-33559-7 , получено 5 апреля 2018 г.

[8] Гаррард, Эндрю. «10.3. Беззнаковые 10-битные числа с плавающей запятой» . Спецификация формата данных Khronos v1.2, ред. 1 . Группа компаний «Хронос» . Проверено 10 августа 2023 г.

[9] Гаррард, Эндрю. «10.2. Беззнаковые 11-битные числа с плавающей запятой» . Спецификация формата данных Khronos v1.2, ред. 1 . Группа компаний «Хронос» . Проверено 10 августа 2023 г.

[10] «Промежуточный отчет рабочей группы IEEE P3109 по 8-битным двоичным форматам с плавающей запятой» (PDF) . Гитхаб . Рабочая группа IEEE P3109. Архивировано из оригинала (PDF) 21 февраля 2024 года . Проверено 7 мая 2024 г.

[11] Шейнифелт, доктор Тед. «Гизмо доктора Шейнифельта, создающее плавающую точку» . Доктор Тед Шейнифелт . Проверено 29 августа 2023 г.

[12] ttps://www.intel.com/content/www/us/en/developer/articles/technical/accelerating-language-model-inference-on-your-pc.html .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

v т и Типы данных
неинтерпретированный	Кусочек Байт Шаг Попробуйте Слово Битовый массив
Числовой	Произвольная точность или bignum Сложный Десятичный Фиксированная точка Плавающая точка Пониженная точность Минипоплавок Половинная точность bfloat16 Одинарная точность Двойная точность Четырехкратная точность Восьмеричная точность Повышенная точность Длинный дабл Целое число подписанность Интервал Рациональный
Указатель	Адрес физический виртуальный Ссылка
Текст	Характер Нить завершающийся нулем
Композитный	Алгебраический тип данных обобщенный Множество Ассоциативный массив Сорт Зависимый Равенство Индуктивный Пересечение Список Объект метаобъект Тип опции Продукт Запись или структура Уточнение Набор Союз отмеченный
Другой	логическое значение Нижний тип Коллекция Перечислимый тип Исключение Тип функции Непрозрачный тип данных Рекурсивный тип данных Семафор Транслировать Строго типизированный идентификатор Тип верха Тип класса Пустой тип Тип устройства Пустота
Связанный темы	Абстрактный тип данных Бокс Структура данных Общий Добрый метакласс Параметрический полиморфизм Примитивный тип данных Интерфейс Подтипирование Тип конструктора Преобразование типов Типовая система Теория типов Переменная