Q-функция

Чтобы узнать о функции фазового пространства, представляющей квантовое состояние, см. представление Husimi Q.

График Q-функции.

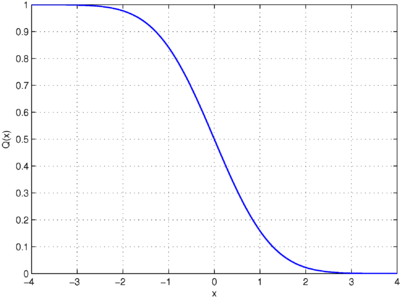
В статистике Q -функция — это хвостовая функция распределения стандартного нормального распределения . Другими словами, $Q(x)$ - вероятность того, что нормальная (гауссова) случайная величина получит значение, большее, чем $x$ стандартные отклонения. Эквивалентно, $Q(x)$ — вероятность того, что стандартная нормальная случайная величина примет значение, большее, чем $x$.

Если $Y$ представляет собой гауссову случайную величину со средним значением $\mu$ и дисперсия $\sigma ^{2}$, затем $X={\frac {Y-\mu }{\sigma }}$ является стандартным нормальным и

$P(Y>y)=P(X>x)=Q(x)$

где $x={\frac {y-\mu }{\sigma }}$.

Другие определения Q -функции, все из которых являются простыми преобразованиями нормальной кумулятивной функции распределения , также используются иногда.

Из-за своей связи с кумулятивной функцией распределения нормального распределения Q -функция также может быть выражена через функцию ошибок , которая является важной функцией в прикладной математике и физике.

Определение и основные свойства

Формально Q -функция определяется как

$Q(x)={\frac {1}{\sqrt {2\pi }}}\int _{x}^{\infty }\exp \left(-{\frac {u^{2}}{2}}\right)\,du.$

Таким образом,

$Q(x)=1-Q(-x)=1-\Phi (x)\,\!,$

где $\Phi (x)$ — кумулятивная функция распределения стандартного нормального распределения Гаусса .

Q -функция может быть выражена через функцию ошибок или дополнительную функцию ошибок, как

${\begin{aligned}Q(x)&={\frac {1}{2}}\left({\frac {2}{\sqrt {\pi }}}\int _{x/{\sqrt {2}}}^{\infty }\exp \left(-t^{2}\right)\,dt\right)\\&={\frac {1}{2}}-{\frac {1}{2}}\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)~~{\text{ -or-}}\\&={\frac {1}{2}}\operatorname {erfc} \left({\frac {x}{\sqrt {2}}}\right).\end{aligned}}$

Альтернативная форма Q -функции, известная как формула Крейга, в честь ее первооткрывателя, выражается как:

$Q(x)={\frac {1}{\pi }}\int _{0}^{\frac {\pi }{2}}\exp \left(-{\frac {x^{2}}{2\sin ^{2}\theta }}\right)d\theta .$

Это выражение действительно только для положительных значений x , но его можно использовать в сочетании с Q ( x ) = 1 - Q (- x ) для получения Q ( x ) для отрицательных значений. Эта форма выгодна тем, что область интегрирования фиксирована и конечна.

Формула Крейга позже была расширена Бенадом (2020). для Q -функции суммы двух неотрицательных переменных следующим образом:

Q-функция, построенная на комплексной плоскости

$Q(x+y)={\frac {1}{\pi }}\int _{0}^{\frac {\pi }{2}}\exp \left(-{\frac {x^{2}}{2\sin ^{2}\theta }}-{\frac {y^{2}}{2\cos ^{2}\theta }}\right)d\theta ,\quad x,y\geqslant 0.$

Границы и приближения

• - функция Q не является элементарной функцией . Однако он может быть ограничен сверху и снизу, как

$\left({\frac {x}{1+x^{2}}}\right)\phi (x)<Q(x)<{\frac {\phi (x)}{x}},\qquad x>0,$

где $\phi (x)$ — функция плотности стандартного нормального распределения, и при больших x границы становятся все более жесткими .

Используя замену v = u ² /2 верхняя граница получается следующим образом:

$Q(x)=\int _{x}^{\infty }\phi (u)\,du<\int _{x}^{\infty }{\frac {u}{x}}\phi (u)\,du=\int _{\frac {x^{2}}{2}}^{\infty }{\frac {e^{-v}}{x{\sqrt {2\pi }}}}\,dv=-{\biggl .}{\frac {e^{-v}}{x{\sqrt {2\pi }}}}{\biggr |}_{\frac {x^{2}}{2}}^{\infty }={\frac {\phi (x)}{x}}.$

Аналогично, используя $\phi '(u)=-u\phi (u)$ и правило фактора ,

$\left(1+{\frac {1}{x^{2}}}\right)Q(x)=\int _{x}^{\infty }\left(1+{\frac {1}{x^{2}}}\right)\phi (u)\,du>\int _{x}^{\infty }\left(1+{\frac {1}{u^{2}}}\right)\phi (u)\,du=-{\biggl .}{\frac {\phi (u)}{u}}{\biggr |}_{x}^{\infty }={\frac {\phi (x)}{x}}.$

Решение для Q ( x ) дает нижнюю оценку.

Среднее геометрическое верхней и нижней границы дает подходящее приближение для $Q(x)$:

$Q(x)\approx {\frac {\phi (x)}{\sqrt {1+x^{2}}}},\qquad x\geq 0.$

• Более жесткие границы и приближения $Q(x)$ также может быть получено путем оптимизации следующего выражения

${\tilde {Q}}(x)={\frac {\phi (x)}{(1-a)x+a{\sqrt {x^{2}+b}}}}.$

Для $x\geq 0$, лучшая верхняя оценка дается выражением $a=0.344$ и $b=5.334$ с максимальной абсолютной относительной ошибкой 0,44%. Аналогично, наилучшее приближение дается выражением $a=0.339$ и $b=5.510$ с максимальной абсолютной относительной погрешностью 0,27%. Наконец, лучшая нижняя оценка дается выражением $a=1/\pi$ и $b=2\pi$ с максимальной абсолютной относительной ошибкой 1,17%.

• Граница Чернова -функции Q равна

$Q(x)\leq e^{-{\frac {x^{2}}{2}}},\qquad x>0$

• Улучшенные экспоненциальные оценки и чисто экспоненциальное приближение:

$Q(x)\leq {\tfrac {1}{4}}e^{-x^{2}}+{\tfrac {1}{4}}e^{-{\frac {x^{2}}{2}}}\leq {\tfrac {1}{2}}e^{-{\frac {x^{2}}{2}}},\qquad x>0$

$Q(x)\approx {\frac {1}{12}}e^{-{\frac {x^{2}}{2}}}+{\frac {1}{4}}e^{-{\frac {2}{3}}x^{2}},\qquad x>0$

• Вышеизложенное было обобщено Танашем и Риихоненом (2020). кто это показал $Q(x)$ могут быть точно аппроксимированы или ограничены

${\tilde {Q}}(x)=\sum _{n=1}^{N}a_{n}e^{-b_{n}x^{2}}.$

В частности, они представили систематическую методологию решения числовых коэффициентов. $\{(a_{n},b_{n})\}_{n=1}^{N}$ которые дают минимаксное приближение или оценку: $Q(x)\approx {\tilde {Q}}(x)$, $Q(x)\leq {\tilde {Q}}(x)$, или $Q(x)\geq {\tilde {Q}}(x)$ для $x\geq 0$. С примерами коэффициентов, приведенными в таблице в статье для $N=20$относительная и абсолютная погрешности аппроксимации не превышают $2.831\cdot 10^{-6}$ и $1.416\cdot 10^{-6}$, соответственно. Коэффициенты $\{(a_{n},b_{n})\}_{n=1}^{N}$ для многих вариаций экспоненциальных приближений и оценок до $N=25$ были выпущены в открытый доступ в виде комплексного набора данных.

• Еще одно приближение $Q(x)$ для $x\in [0,\infty )$ предоставлено Карагианнидисом и Лиумпасом (2007). который показал для соответствующего выбора параметров $\{A,B\}$ что

$f(x;A,B)={\frac {\left(1-e^{-Ax}\right)e^{-x^{2}}}{B{\sqrt {\pi }}x}}\approx \operatorname {erfc} \left(x\right).$

Абсолютная ошибка между $f(x;A,B)$ и $\operatorname {erfc} (x)$ за пределами диапазона $[0,R]$ минимизируется путем оценки

$\{A,B\}={\underset {\{A,B\}}{\arg \min }}{\frac {1}{R}}\int _{0}^{R}|f(x;A,B)-\operatorname {erfc} (x)|dx.$

С использованием $R=20$ и численно интегрируя, они обнаружили, что минимальная ошибка возникает, когда $\{A,B\}=\{1.98,1.135\},$ что дало хорошее приближение для $\forall x\geq 0.$

Подставив эти значения и используя связь между $Q(x)$ и $\operatorname {erfc} (x)$ сверху дает

$Q(x)\approx {\frac {\left(1-e^{\frac {-1.98x}{\sqrt {2}}}\right)e^{-{\frac {x^{2}}{2}}}}{1.135{\sqrt {2\pi }}x}},x\geq 0.$

Альтернативные коэффициенты также доступны для вышеупомянутого «приближения Карагианнидиса – Лиумпаса» для адаптации точности для конкретного приложения или преобразования ее в жесткую границу.

• Более точное и удобное приближение $Q(x)$ за положительные аргументы $x\in [0,\infty )$ предоставлено Лопесом-Бенитесом и Касадевалем (2011). на основе показательной функции второго порядка:

$Q(x)\approx e^{-ax^{2}-bx-c},\qquad x\geq 0.$

Коэффициенты подгонки $(a,b,c)$ может быть оптимизирован по любому желаемому диапазону аргументов, чтобы минимизировать сумму квадратных ошибок ( $a=0.3842$, $b=0.7640$, $c=0.6964$ для $x\in [0,20]$) или минимизировать максимальную абсолютную ошибку ( $a=0.4920$, $b=0.2887$, $c=1.1893$ для $x\in [0,20]$). Это приближение дает некоторые преимущества, такие как хороший компромисс между точностью и аналитической доступностью (например, расширение до любой произвольной степени $Q(x)$ тривиально и не меняет алгебраическую форму приближения).

Обратный Q

Обратная Q -функция может быть связана с обратными функциями ошибок :

$Q^{-1}(y)={\sqrt {2}}\ \mathrm {erf} ^{-1}(1-2y)={\sqrt {2}}\ \mathrm {erfc} ^{-1}(2y)$

Функция $Q^{-1}(y)$ находит применение в цифровых коммуникациях. Обычно он выражается в дБ и обычно называется добротностью :

$\mathrm {Q{\text{-}}factor} =20\log _{10}\!\left(Q^{-1}(y)\right)\!~\mathrm {dB}$

где y — коэффициент битовых ошибок (BER) анализируемого сигнала с цифровой модуляцией. Например, для квадратурной фазовой манипуляции (QPSK) в аддитивном белом гауссовском шуме Q-фактор, определенный выше, совпадает со значением в дБ отношения сигнал/шум , что дает коэффициент ошибок по битам, равный y .

Q-фактор в зависимости от частоты ошибок по битам (BER).

Ценности

- функция Q хорошо табулирована и может быть вычислена непосредственно в большинстве пакетов математического программного обеспечения, таких как R и доступных в Python , MATLAB и Mathematica . Некоторые значения Q -функции приведены ниже для справки.

К (0,0)	0.500000000	1/2.0000
К (0,1)	0.460172163	1/2.1731
Вопрос (0,2)	0.420740291	1/2.3768
Вопрос (0,3)	0.382088578	1/2.6172
Вопрос (0,4)	0.344578258	1/2.9021
Вопрос (0,5)	0.308537539	1/3.2411
Вопрос (0,6)	0.274253118	1/3.6463
Вопрос (0,7)	0.241963652	1/4.1329
Вопрос (0,8)	0.211855399	1/4.7202
Вопрос (0,9)	0.184060125	1/5.4330

Вопрос (1,0)	0.158655254	1/6.3030
Вопрос (1.1)	0.135666061	1/7.3710
Вопрос (1.2)	0.115069670	1/8.6904
Вопрос (1.3)	0.096800485	1/10.3305
Вопрос (1,4)	0.080756659	1/12.3829
Вопрос (1,5)	0.066807201	1/14.9684
Вопрос (1,6)	0.054799292	1/18.2484
Вопрос (1,7)	0.044565463	1/22.4389
Вопрос (1,8)	0.035930319	1/27.8316
Вопрос (1,9)	0.028716560	1/34.8231

Вопрос (2,0)	0.022750132	1/43.9558
Вопрос (2.1)	0.017864421	1/55.9772
Вопрос (2.2)	0.013903448	1/71.9246
Вопрос (2.3)	0.010724110	1/93.2478
Вопрос (2.4)	0.008197536	1/121.9879
Вопрос (2,5)	0.006209665	1/161.0393
Вопрос (2,6)	0.004661188	1/214.5376
Вопрос (2,7)	0.003466974	1/288.4360
Вопрос (2,8)	0.002555130	1/391.3695
Вопрос (2,9)	0.001865813	1/535.9593

Вопрос (3,0)	0.001349898	1/740.7967
Вопрос (3.1)	0.000967603	1/1033.4815
Вопрос (3.2)	0.000687138	1/1455.3119
Вопрос (3.3)	0.000483424	1/2068.5769
Вопрос (3.4)	0.000336929	1/2967.9820
Вопрос (3,5)	0.000232629	1/4298.6887
Вопрос (3,6)	0.000159109	1/6285.0158
Вопрос (3,7)	0.000107800	1/9276.4608
Вопрос (3,8)	0.000072348	1/13822.0738
Вопрос (3,9)	0.000048096	1/20791.6011
Вопрос (4,0)	0.000031671	1/31574.3855

Обобщение на большие размерности

Q -функция может быть обобщена на более высокие размерности:

$Q(\mathbf {x} )=\mathbb {P} (\mathbf {X} \geq \mathbf {x} ),$

где $\mathbf {X} \sim {\mathcal {N}}(\mathbf {0} ,\,\Sigma )$ следует многомерному нормальному распределению с ковариацией $\Sigma$ и порог имеет вид $\mathbf {x} =\gamma \Sigma \mathbf {l} ^{*}$ для некоторого положительного вектора $\mathbf {l} ^{*}>\mathbf {0}$ и положительная константа $\gamma >0$. Как и в одномерном случае, простой аналитической формулы для Q -функции не существует. Тем не менее, Q -функция может быть аппроксимирована сколь угодно хорошо как $\gamma$ становится все больше и больше.