Иллюстрация центральной предельной теоремы

В теории вероятностей центральная предельная теорема (ЦПТ) утверждает, что во многих ситуациях, когда добавляются независимые и одинаково распределенные случайные величины, их правильно нормализованная сумма стремится к нормальному распределению. В данной статье приведены две иллюстрации этой теоремы. Оба включают сумму независимых и одинаково распределенных случайных величин и показывают, как распределение вероятностей суммы приближается к нормальному распределению по мере увеличения количества членов в сумме.

Первая иллюстрация связана с непрерывным распределением вероятностей , для которого случайные величины имеют функцию плотности вероятности . Вторая иллюстрация, для которой большая часть вычислений может быть выполнена вручную, включает дискретное распределение вероятностей , которое характеризуется функцией массы вероятности .

Иллюстрация непрерывного случая

Плотность суммы двух независимых действительных случайных величин равна свертке функций плотности исходных переменных.

Таким образом, плотность суммы m + n членов последовательности независимых одинаково распределенных переменных равна свертке плотностей сумм m членов и n членов. В частности, плотность суммы n +1 слагаемых равна свертке плотности суммы n слагаемых с исходной плотностью («сумма» 1 слагаемого).

Функция плотности вероятности показана на первом рисунке ниже. Тогда плотности сумм двух, трех и четырех независимых одинаково распределенных переменных , каждая из которых имеет исходную плотность, показаны на следующих рисунках.Если исходная плотность представляет собой кусочный полином , как в примере, то такими же являются и суммарные плотности все более высокой степени. Хотя исходная плотность далека от нормальной, плотность суммы всего нескольких переменных с этой плотностью гораздо более гладкая и имеет некоторые качественные особенности нормальной плотности .

Свертки были вычислены с помощью дискретного преобразования Фурье . Был построен список значений y = f ( x ₀ + k ∆ x ), где f — исходная функция плотности, ∆ x примерно равна 0,002, а k равно от 0 до 1000. Дискретное преобразование Y Фурье y было вычислено. Тогда свертка f сама с собой пропорциональна обратному дискретному преобразованию Фурье поточечного произведения Y с самой собой.

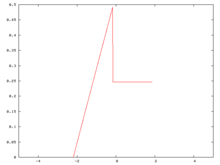
Исходная функция плотности вероятности

Начнем с функции плотности вероятности. Эта функция, хотя и прерывистая, но далеко не самый патологический пример, который можно было бы создать. Это кусочный полином с частями степени 0 и 1. Среднее значение этого распределения равно 0, а его стандартное отклонение равно 1.

Функция плотности вероятности суммы двух слагаемых

Затем мы вычисляем плотность суммы двух независимых переменных , каждая из которых имеет указанную выше плотность. Плотность суммы представляет собой свертку указанной выше плотности с самой собой.

Сумма двух переменных имеет среднее значение 0.Плотность, показанная на рисунке справа, была изменена на ${\sqrt {2}}$ , так что его стандартное отклонение равно 1.

Эта плотность уже более гладкая, чем оригинал.Имеются явные комки, соответствующие интервалам , на которых определялась исходная плотность.

Функция плотности вероятности суммы трех слагаемых

Затем мы вычисляем плотность суммы трех независимых переменных, каждая из которых имеет указанную выше плотность. Плотность суммы — это свертка первой плотности со второй.

Сумма трех переменных имеет среднее значение 0.Плотность, показанная на рисунке справа, была масштабирована на √ 3 , так что ее стандартное отклонение равно 1.

Эта плотность еще более гладкая, чем предыдущая.На этом рисунке комочки едва заметны.

Функция плотности вероятности суммы четырех слагаемых

Наконец, мы вычисляем плотность суммы четырех независимых переменных, каждая из которых имеет указанную выше плотность. Плотность суммы — это свертка первой плотности с третьей (или второй плотности с самой собой).

Сумма четырех переменных имеет среднее значение 0.Плотность, показанная на рисунке справа, была масштабирована на √ 4 , так что ее стандартное отклонение равно 1.

Эта плотность качественно очень похожа на нормальную плотность .Никакие комочки на глаз не различимы.

Иллюстрация дискретного случая

В этом разделе центральная предельная теорема иллюстрируется на примере, для которого вычисления можно быстро выполнить вручную на бумаге, в отличие от более ресурсоемкого примера из предыдущего раздела.

Исходная функция массы вероятности

Предположим, что распределение вероятностей дискретной случайной величины X присваивает равные веса 1, 2 и 3:

X=\left\{{\begin{matrix}1&{\mbox{with}}\ {\mbox{probability}}\ 1/3,\\2&{\mbox{with}}\ {\mbox{probability}}\ 1/3,\\3&{\mbox{with}}\ {\mbox{probability}}\ 1/3.\end{matrix}}\right.

Массовую функцию вероятности случайной величины X можно изобразить следующей гистограммой :

Очевидно, что это совсем не похоже на колоколообразную кривую нормального распределения. Сравните приведенное выше с изображениями ниже.

Массовая функция вероятности суммы двух слагаемых

Теперь рассмотрим сумму двух независимых копий X :

\left\{{\begin{matrix}1+1&=&2\\1+2&=&3\\1+3&=&4\\2+1&=&3\\2+2&=&4\\2+3&=&5\\3+1&=&4\\3+2&=&5\\3+3&=&6\end{matrix}}\right\}=\left\{{\begin{matrix}2&{\mbox{with}}\ {\mbox{probability}}\ 1/9\\3&{\mbox{with}}\ {\mbox{probability}}\ 2/9\\4&{\mbox{with}}\ {\mbox{probability}}\ 3/9\\5&{\mbox{with}}\ {\mbox{probability}}\ 2/9\\6&{\mbox{with}}\ {\mbox{probability}}\ 1/9\end{matrix}}\right\}

Массовую функцию вероятности этой суммы можно изобразить следующим образом:

Это все еще не очень похоже на колоколообразную кривую, но, как и колоколообразная кривая и в отличие от функции массы вероятности самого X , она выше в середине, чем в двух хвостах.

Массовая функция вероятности суммы трех слагаемых

Теперь рассмотрим сумму трех независимых копий этой случайной величины:

\left\{{\begin{matrix}1+1+1&=&3\\1+1+2&=&4\\1+1+3&=&5\\1+2+1&=&4\\1+2+2&=&5\\1+2+3&=&6\\1+3+1&=&5\\1+3+2&=&6\\1+3+3&=&7\\2+1+1&=&4\\2+1+2&=&5\\2+1+3&=&6\\2+2+1&=&5\\2+2+2&=&6\\2+2+3&=&7\\2+3+1&=&6\\2+3+2&=&7\\2+3+3&=&8\\3+1+1&=&5\\3+1+2&=&6\\3+1+3&=&7\\3+2+1&=&6\\3+2+2&=&7\\3+2+3&=&8\\3+3+1&=&7\\3+3+2&=&8\\3+3+3&=&9\end{matrix}}\right\}=\left\{{\begin{matrix}3&{\mbox{with}}\ {\mbox{probability}}\ 1/27\\4&{\mbox{with}}\ {\mbox{probability}}\ 3/27\\5&{\mbox{with}}\ {\mbox{probability}}\ 6/27\\6&{\mbox{with}}\ {\mbox{probability}}\ 7/27\\7&{\mbox{with}}\ {\mbox{probability}}\ 6/27\\8&{\mbox{with}}\ {\mbox{probability}}\ 3/27\\9&{\mbox{with}}\ {\mbox{probability}}\ 1/27\end{matrix}}\right\}

Массовую функцию вероятности этой суммы можно изобразить следующим образом:

Мало того, что в центре она больше, чем у хвостов, но по мере продвижения к центру от любого хвоста наклон сначала увеличивается, а затем уменьшается, как и в случае с колоколообразной кривой.

Степень ее сходства с колоколообразной кривой можно количественно оценить следующим образом. Учитывать

Пр ₁ + X₂ + X₃(

Насколько это близко к тому, что нормальное дало бы приближение? Легко видеть, что ожидаемое значение Y = X ₁ + X ₂ + X ₃ равно 6, а стандартное отклонение Y представляет собой квадратный корень из 2 . Поскольку Y ≤ 7 (слабое неравенство) тогда и только тогда, когда Y < 8 (строгое неравенство), мы используем поправку на непрерывность и ищем

{\mbox{Pr}}(Y\leq 7.5)={\mbox{P}}\left({Y-6 \over {\sqrt {2}}}\leq {7.5-6 \over {\sqrt {2}}}\right)={\mbox{Pr}}(Z\leq 1.0606602\dots )=0.85558\dots

где Z имеет стандартное нормальное распределение. Разница между 0,85185... и 0,85558... кажется удивительно малой, если учесть, что количество добавленных независимых случайных величин составило всего три.

Массовая функция вероятности суммы 1000 членов

На следующем изображении показан результат моделирования на основе примера, представленного на этой странице. Извлечение из равномерного распределения повторяется 1000 раз и результаты суммируются.

Поскольку моделирование основано на методе Монте-Карло , процесс повторяется 10 000 раз. Результаты показывают, что распределение суммы 1000 однородных экстракций очень хорошо напоминает колоколообразную кривую.

Внешние ссылки