Теорема Кирхгофа

В математической области теории графов теорема Кирхгофа или теорема Кирхгофа о матричном дереве, в честь Густава Кирхгофа, теорему о количестве остовных деревьев в графе , показывающую, что это число может быть вычислено за полиномиальное время из определителя подматрицы названная представляет собой Матрица Лапласа графа; в частности, это число равно любому кофактору матрицы Лапласа. Теорема Кирхгофа является обобщением формулы Кэли , которая определяет количество остовных деревьев в полном графе .

Теорема Кирхгофа основана на понятии матрицы Лапласа графа, которая равна разности между матрицей степеней графа (диагональной матрицей со степенями вершин на диагоналях) и ее матрицей смежности ((0,1)-матрицей с 1 в местах, соответствующих записям, где вершины смежны, и 0 в противном случае).

Для данного связного графа G с n помеченными вершинами пусть λ ₁ , λ ₂ , ..., λ _n₋₁ — ненулевые собственные значения его матрицы Лапласа. Тогда число остовных деревьев группы G равно

t(G)={\frac {1}{n}}\lambda _{1}\lambda _{2}\cdots \lambda _{n-1}\,.

Английский перевод оригинальной статьи Кирхгофа 1847 года был сделан Дж. Б. О'Тулом и опубликован в 1958 году. ^[1]

Пример использования теоремы о матричном дереве

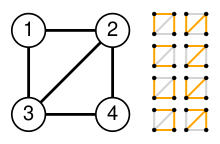
Сначала постройте матрицу Лапласа Q для примера ромбовидного графа G (см. изображение справа):

Q=\left[{\begin{array}{rrrr}2&-1&-1&0\\-1&3&-1&-1\\-1&-1&3&-1\\0&-1&-1&2\end{array}}\right].

Далее построим матрицу Q ^* удалив любую строку и любой столбец из Q . Например, удаление строки 1 и столбца 1 дает

Q^{\ast }=\left[{\begin{array}{rrr}3&-1&-1\\-1&3&-1\\-1&-1&2\end{array}}\right].

Наконец, определитель Q возьмем ^* чтобы получить t ( G ), которое для ромбовидного графа равно 8. (Обратите внимание, что t ( G ) — это (1,1) -комножитель Q в этом примере.)

Схема доказательства

(Приведенное ниже доказательство основано на формуле Коши – Бине . Элементарное индукционное обоснование теоремы Кирхгофа можно найти на странице 654 книги Мура (2011). ^[2])

Прежде всего обратите внимание, что матрица Лапласа обладает свойством: сумма ее элементов в любой строке и любом столбце равна 0. Таким образом, мы можем преобразовать любой минор в любой другой минор, добавляя строки и столбцы, переключая их и умножая строку или столбец. на −1. Таким образом, кофакторы одинаковы с точностью до знака, и можно убедиться, что на самом деле они имеют одинаковый знак.

Мы продолжаем показывать, что определитель минора M ₁₁ подсчитывает количество остовных деревьев. Пусть n — количество вершин графа, а m — количество его ребер. Матрица инцидентности E представляет собой матрицу размером n - m , которую можно определить следующим образом: предположим, что ( i , j ) является k -м ребром графа, и что i < j . Тогда E _ik = 1, E _jk = −1, а все остальные записи в столбце k равны 0 ( инцидентности для понимания этой модифицированной матрицы E см. Ориентированную матрицу инцидентности ). Для предыдущего примера (с n = 4 и m = 5):

E={\begin{bmatrix}1&1&0&0&0\\-1&0&1&1&0\\0&-1&-1&0&1\\0&0&0&-1&-1\\\end{bmatrix}}.

Напомним, что лапласиан L можно разложить на произведение матрицы инцидентности и ее транспонирования, т. е. L = EE ^Т. Далее, пусть F — матрица E с удаленной первой строкой, так что FF ^Т = М ₁₁ .

Теперь формула Коши–Бине позволяет записать

\det \left(M_{11}\right)=\sum _{S}\det \left(F_{S}\right)\det \left(F_{S}^{\mathrm {T} }\right)=\sum _{S}\det \left(F_{S}\right)^{2}

где S пробегает подмножества [ m ] размера n - 1, а FS _с обозначает матрицу ( n - 1) на ( n - 1), столбцы которой являются столбцами F индексом в S . Тогда каждое S определяет n - 1 ребро исходного графа, и можно показать, что эти ребра порождают остовное дерево тогда и только тогда, когда определитель равен _FS +1 или -1, и что они не индуцируют остовное дерево. тогда и только тогда, когда определитель равен 0. Это завершает доказательство.

Частные случаи и обобщения

Формула Кэли

Формула Кэли следует из теоремы Кирхгофа как частный случай, поскольку каждый вектор с 1 в одном месте, -1 в другом месте и 0 в другом месте является собственным вектором матрицы Лапласа полного графа с соответствующим собственным значением n . Эти векторы вместе охватывают пространство размерности n - 1, поэтому других ненулевых собственных значений нет.

В качестве альтернативы обратите внимание, что, поскольку формула Кэли подсчитывает количество различных помеченных деревьев полного графа K _n, нам необходимо вычислить любой кофактор матрицы Лапласа K _n . Матрица Лапласа в этом случае равна

{\begin{bmatrix}n-1&-1&\cdots &-1\\-1&n-1&\cdots &-1\\\vdots &\vdots &\ddots &\vdots \\-1&-1&\cdots &n-1\\\end{bmatrix}}.

Любой кофактор приведенной выше матрицы равен n ^н⁻², что является формулой Кэли.

Теорема Кирхгофа для мультиграфов

Теорема Кирхгофа справедлива для мультиграфов и ; матрица Q модифицируется следующим образом:

Запись q _i,j равна − m , где m — количество ребер между i и j ;
при подсчете степени вершины все петли . исключаются

Формула Кэли для полного мультиграфа: m ^{п -1}( н ^{п -1}-( п -1) п ^{п -2}) теми же методами, что и выше, поскольку простой граф — это мультиграф с m = 1.

Явное перечисление связующих деревьев

Теорему Кирхгофа можно усилить, изменив определение матрицы Лапласа. Вместо того, чтобы просто считать ребра, исходящие из каждой вершины или соединяющие пару вершин, пометьте каждое ребро неопределенной величиной и пусть ( i , j )-я запись модифицированной матрицы Лапласа будет суммой неопределенных величин, соответствующих ребрам между i -th и j -th вершины, когда i не равно j , и отрицательная сумма по всем неопределенным, соответствующим ребрам, исходящим из i -й вершины, когда i равно j .

Определитель модифицированной матрицы Лапласа путем удаления любой строки и столбца (аналогично нахождению количества остовных деревьев из исходной матрицы Лапласа), приведенный выше, тогда представляет собой однородный полином (полином Кирхгофа) от неопределенных величин, соответствующих ребрам графа. . После сбора членов и выполнения всех возможных сокращений каждый моном в полученном выражении представляет собой остовное дерево, состоящее из ребер, соответствующих неопределенным числам, входящим в этот моном. Таким образом, можно получить явное перечисление всех остовных деревьев графа, просто вычислив определитель.

Доказательство этой версии теоремы см. в Bollobás (1998). ^[3]

Матроиды

Опорные деревья графа образуют основания графического матроида , поэтому теорема Кирхгофа дает формулу для подсчета количества оснований в графическом матроиде. Тот же метод можно использовать и для подсчета количества оснований в обычных матроидах — обобщении графических матроидов ( Маурер, 1976 ).

Теорема Кирхгофа для ориентированных мультиграфов

Теорему Кирхгофа можно модифицировать, чтобы подсчитать количество ориентированных остовных деревьев в ориентированных мультиграфах.Матрица Q строится следующим образом:

Запись q _i,j для различных i и j равна − m , где m — количество ребер от i до j ;
Запись q _i,i равна входной степени i минус количество петель в i .

Количество ориентированных остовных деревьев с корнем в вершине i является определителем матрицы, полученной путем удаления i -й строки и столбца Q.

Подсчет охватывающих k -компонентных лесов

Теорему Кирхгофа можно обобщить для подсчета $k$ -компонентных остовных лесов в невзвешенном графе. ^[4] K $k$ -компонентный остовный лес — это подграф с $,$ связными компонентами который содержит все вершины и не имеет циклов, т. е. между каждой парой вершин существует не более одного пути. Учитывая такой лес F со связными компонентами ${\textstyle F_{1},\dots ,F_{k}}$ , определите его вес ${\textstyle w(F)=|V(F_{1})|\cdot \dots \cdot |V(F_{k})|}$ быть произведением количества вершин в каждом компоненте. Затем

\sum _{F}w(F)=q_{k},

где сумма ведется по всем $k$ -компонентным остовным лесам и ${\textstyle q_{k}}$ коэффициент ${\textstyle x^{k}}$ полинома

(x+\lambda _{1})\dots (x+\lambda _{n-1})x.

Последний множитель в полиноме обусловлен нулевым собственным значением ${\textstyle \lambda _{n}=0}$ . Более явно, число ${\textstyle q_{k}}$ может быть вычислено как

q_{k}=\sum _{\{i_{1},\dots ,i_{n-k}\}\subset \{1\dots n-1\}}\lambda _{i_{1}}\dots \lambda _{i_{n-k}}.

где сумма ведется по всем n – k -элементным подмножествам ${\textstyle \{1,\dots ,n\}}$ . Например

${\begin{aligned}q_{n-1}&=\lambda _{1}+\dots +\lambda _{n-1}=\mathrm {tr} Q=2|E|\\q_{n-2}&=\lambda _{1}\lambda _{2}+\lambda _{1}\lambda _{3}+\dots +\lambda _{n-2}\lambda _{n-1}\\q_{2}&=\lambda _{1}\dots \lambda _{n-2}+\lambda _{1}\dots \lambda _{n-3}\lambda _{n-1}+\dots +\lambda _{2}\dots \lambda _{n-1}\\q_{1}&=\lambda _{1}\dots \lambda _{n-1}\\\end{aligned}}$

Поскольку остовный лес с n –1 компонентами соответствует одному ребру, случай k = n – 1 утверждает, что сумма собственных значений Q в два раза превышает количество ребер. Случай k = 1 соответствует исходной теореме Кирхгофа, поскольку вес каждого остовного дерева равен n .

Доказательство можно провести аналогично доказательству теоремы Кирхгофа. обратимый ${\textstyle (n-k)\times (n-k)}$ Подматрица матрицы инцидентности биективно соответствует k -компонентному остовному лесу с выбором вершины для каждого компонента.

Коэффициенты ${\textstyle q_{k}}$ до знака коэффициентов многочлена Q характеристического .

См. также

Ссылки

^ О'Тул, Дж. Б. «О решении уравнений, полученных в результате исследования линейного распределения гальванических токов». IRE Транзакции по теории цепей . 5 (1): 4–7. дои : 10.1109/TCT.1958.1086426 .
^ Мур, Кристофер (2011). Характер вычислений . Оксфорд, Англия, Нью-Йорк: Издательство Оксфордского университета. ISBN 978-0-19-923321-2 . OCLC 180753706 .
^ Боллобас, Бела (1998). Современная теория графов . Нью-Йорк: Спрингер. дои : 10.1007/978-1-4612-0619-4 . ISBN 978-0-387-98488-9 .
^ Биггс, Н. (1993). Алгебраическая теория графов . Издательство Кембриджского университета.

Харрис, Джон М.; Херст, Джеффри Л.; Моссингхофф, Майкл Дж. (2008), Комбинаторика и теория графов , Тексты для студентов по математике (2-е изд.), Springer .
Маурер, Стивен Б. (1976), «Матричные обобщения некоторых теорем о деревьях, циклах и коциклах в графах», SIAM Journal on Applied Mathematics , 30 (1): 143–148, doi : 10.1137/0130017 , MR 0392635 .
Тутт, WT (2001), Теория графов , Издательство Кембриджского университета, стр. 138, ISBN 978-0-521-79489-3 .
Чайкен, С.; Клейтман, Д. (1978), «Теоремы о матричном дереве», Журнал комбинаторной теории, серия A , 24 (3): 377–381, doi : 10.1016/0097-3165(78)90067-5 , ISSN 0097-3165

Внешние ссылки

Доказательство теоремы Кирхгофа

[1] О'Тул, Дж. Б. «О решении уравнений, полученных в результате исследования линейного распределения гальванических токов». IRE Транзакции по теории цепей . 5 (1): 4–7. дои : 10.1109/TCT.1958.1086426 .

[Moore_2011_p._654-2] Мур, Кристофер (2011). Характер вычислений . Оксфорд, Англия, Нью-Йорк: Издательство Оксфордского университета. ISBN 978-0-19-923321-2 . OCLC 180753706 .

[3] Боллобас, Бела (1998). Современная теория графов . Нью-Йорк: Спрингер. дои : 10.1007/978-1-4612-0619-4 . ISBN 978-0-387-98488-9 .

[4] Биггс, Н. (1993). Алгебраическая теория графов . Издательство Кембриджского университета.

[1]

[2]

[3]

[4]