Энтропийное значение под угрозой
В финансовой математике и стохастической оптимизации концепция меры риска используется для количественной оценки риска, связанного со случайным результатом или рисковой позицией. До сих пор было предложено множество мер риска, каждая из которых имеет определенные характеристики. Энтропийное значение риска ( EVaR ) — это последовательная мера риска, введенная Ахмади-Джавидом, [1] [2] которое является верхней границей значения риска (VaR) и условного значения риска (CVaR), полученных из неравенства Чернова . EVAR также можно представить, используя концепцию относительной энтропии . Из-за связи с VaR и относительной энтропией эта мера риска называется «энтропийной величиной риска». EVAR был разработан для устранения некоторых вычислительных недостатков. [ нужны разъяснения ] ЦВАР. Черпая вдохновение из двойного представительства EVAR, Ахмади-Джавид [1] [2] разработал широкий класс последовательных мер риска , названных g-энтропийными мерами риска . И CVaR, и EVaR являются членами этого класса.
Определение
[ редактировать ]Позволять быть вероятностным пространством с набор всех простых событий, а -алгебра подмножеств и мера вероятностная на . Позволять быть случайной величиной и — множество всех измеримых по Борелю функций чья моментообразующая функция существует для всех . Энтропийное значение риска (EVaR) с уровнем уверенности определяется следующим образом:
| ( 1 ) |
В финансах случайная величина в приведенном выше уравнении используется для моделирования потерь портфеля.
Рассмотрим неравенство Чернова
| ( 2 ) |
Решение уравнения для приводит к
Рассматривая уравнение ( 1 ), мы видим, что
который показывает связь между EVAR и неравенством Чернова. Стоит отметить, что — это энтропийная мера риска или экспоненциальная премия , которая представляет собой концепцию, используемую в финансах и страховании соответственно.
Позволять — множество всех измеримых по Борелю функций чья моментообразующая функция существует для всех . Двойное представление (или устойчивое представление) EVAR выглядит следующим образом:
| ( 3 ) |
где и представляет собой набор вероятностных мер по с . Обратите внимание, что
это энтропия относительная относительно также называется расходимостью Кульбака-Лейблера . Двойное представление EVAR раскрывает причину его названия.
Характеристики
[ редактировать ]- EVAR является последовательным показателем риска.
- Момент-генерирующая функция может быть представлено EVaR: для всех и
| ( 4 ) |
- Для , для всех тогда и только тогда, когда для всех .
- Мера энтропийного риска с параметром может быть представлено посредством EVaR: для всех и
| ( 5 ) |
- EVAR с уровнем уверенности — максимально точная верхняя граница, которую можно получить из неравенства Чернова для VaR и CVaR с уровнем достоверности ;
| ( 6 ) |
- Для EVAR справедливо следующее неравенство:
| ( 7 ) |
- где значение ожидаемое и является супремумом существенным , то есть, . Так что держись и .
Примеры
[ редактировать ]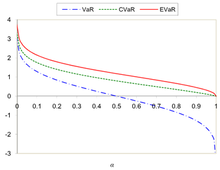
Для
| ( 8 ) |
Для
| ( 9 ) |
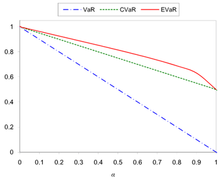
На рисунках 1 и 2 показано сравнение VaR, CVaR и EVAR для и .
Оптимизация
[ редактировать ]Позволять быть мерой риска. Рассмотрим задачу оптимизации
| ( 10 ) |
где это -мерный реальный вектор решения , это -мерный действительный случайный вектор с известным распределением вероятностей и функцией является измеримой по Борелю функцией для всех значений Если тогда задача оптимизации ( 10 ) превращается в:
| ( 11 ) |
Позволять быть носителем случайного вектора Если является выпуклым для всех , то целевая функция задачи ( 11 ) также выпукла. Если имеет форму
| ( 12 ) |
и являются независимыми случайными величинами в , тогда ( 11 ) становится
| ( 13 ) |
который является вычислительно поддающимся . Но в этом случае, если использовать CVaR в задаче ( 10 ), результирующая проблема будет следующей:
| ( 14 ) |
Можно показать, что, увеличивая размерность , задача ( 14 ) вычислительно неразрешима даже для простых случаев. Например, предположим, что являются независимыми дискретными случайными величинами , которые принимают отдельные ценности. Для фиксированных значений и сложность 13 вычисления целевой функции, заданной в задаче ( ) , имеет порядок а время вычисления целевой функции задачи ( 14 ) имеет порядок . Для иллюстрации предположим, что и суммирование двух чисел занимает секунды. Для вычисления целевой функции задачи ( 14 ) необходимо около лет, тогда как оценка целевой функции задачи ( 13 ) занимает около секунды. Это показывает, что состав с EVaR превосходит состав с CVaR (см. [2] для более подробной информации).
Обобщение (г-энтропийные меры риска)
[ редактировать ]Черпая вдохновение из двойного представления EVAR, данного в ( 3 ), можно определить широкий класс теоретико-информационных последовательных мер риска, которые вводятся в. [1] [2] Позволять — выпуклая собственная функция с и быть неотрицательным числом. -энтропийная мера риска с уровнем дивергенции определяется как
| ( 15 ) |
где в котором - обобщенная относительная энтропия относительно . Первичное представление класса -энтропийные меры риска можно получить следующим образом:
| ( 16 ) |
где является сопряженным . рассматривая
| ( 17 ) |
с и , можно вывести формулу EVAR. CVaR также является -энтропийная мера риска, которую можно получить из ( 16 ), полагая
| ( 18 ) |
с и (видеть [1] [3] для более подробной информации).
Для получения дополнительных результатов на -энтропийные меры риска см. [4]
Структура дисциплинированного выпуклого программирования
[ редактировать ]Структура дисциплинированного выпуклого программирования образца EVaR была предложена Cajas. [5] и имеет следующий вид:
| ( 19 ) |
где , и являются переменными; представляет собой экспоненциальный конус; [6] и это количество наблюдений. Если мы определим как вектор весов для ресурсы, матрица доходности и средний вектор активов, мы можем сформулировать минимизацию ожидаемого EVAR при заданном уровне ожидаемой доходности портфеля. следующее.
| ( 20 ) |
Применяя дисциплинированную структуру выпуклого программирования EVAR к распределению несоставных кумулятивных доходов, Cajas [5] предложил задачу оптимизации энтропийной просадки под риском ( EDaR ). Мы можем сформулировать минимизацию ожидаемого EDAR при заданном уровне ожидаемой доходности. следующее:
| ( 21 ) |
где — это переменная, которая представляет собой несложную совокупную доходность портфеля и представляет собой матрицу несложной совокупной доходности активов.
Для других проблем, таких как паритет риска, максимизация соотношения доходности/риска или ограничения на максимальные уровни риска для EVAR и EDAR, вы можете увидеть [5] для более подробной информации.
Преимущество моделей EVAR и EDAR с использованием дисциплинированной среды выпуклого программирования заключается в том, что мы можем использовать такое программное обеспечение, как CVXPY. [7] или МОСЕК [8] смоделировать проблемы оптимизации портфеля. EVAR и EDAR реализованы в пакете Python Riskfolio-Lib. [9]
См. также
[ редактировать ]- Стохастическая оптимизация
- Мера риска
- Последовательная мера риска
- Стоимость под угрозой
- Условная стоимость под угрозой
- Ожидаемый дефицит
- Мера энтропийного риска
- Расхождение Кульбака – Лейблера
- Обобщенная относительная энтропия
Ссылки
[ редактировать ]- ^ Jump up to: а б с д Ахмади-Джавид, Амир (2011). «Теоретико-информационный подход к построению последовательных мер риска». 2011 Международный симпозиум IEEE по материалам теории информации . Санкт-Петербург, Россия: Материалы Международного симпозиума IEEE по теории информации. стр. 2125–2127. дои : 10.1109/ISIT.2011.6033932 . ISBN 978-1-4577-0596-0 . S2CID 8720196 .
- ^ Jump up to: а б с д Ахмади-Джавид, Амир (2012). «Энтропийная ценность риска: новая последовательная мера риска». Журнал теории оптимизации и приложений . 155 (3): 1105–1123. дои : 10.1007/s10957-011-9968-2 . S2CID 46150553 .
- ^ Ахмади-Джавид, Амир (2012). «Дополнение к: Энтропийная ценность риска: новая последовательная мера риска». Журнал теории оптимизации и приложений . 155 (3): 1124–1128. дои : 10.1007/s10957-012-0014-9 . S2CID 39386464 .
- ^ Брейер, Томас; Чисар, Имре (2013). «Измерение риска модели распределения». arXiv : 1301.4832v1 [ q-fin.RM ].
- ^ Jump up to: а б с Кахас, Дэни (24 февраля 2021 г.). «Оптимизация энтропийного портфеля: структура дисциплинированного выпуклого программирования». дои : 10.2139/ssrn.3792520 . S2CID 235319743 .
{{cite journal}}: Для цитирования журнала требуется|journal=( помощь ) - ^ Чарес, Роберт (2009). «Алгоритмы конусов и внутренних точек для структурированной выпуклой оптимизации с использованием степеней и экспонент». S2CID 118322815 .
{{cite web}}: Отсутствует или пусто|url=( помощь ) - ^ "CVXPY" .
- ^ «МОСЕК» .
- ^ «Рискфолио-Либ» . Гитхаб . 18 июля 2022 г.


































![{\displaystyle \alpha \in ]0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d807843c397d6655a0415841bfd2d942aaa9f738)




































![{\displaystyle \min _ {{\boldsymbol {w}}\in {\boldsymbol {W}},t\in \mathbb {R}}\left\lbrace t+{\frac {1}{\alpha }}{ \text{E}}\left[g_{0}({\boldsymbol {w}})+\sum _{i=1}^{m}g_{i}({\boldsymbol {w}})\psi _{i}-t\right]_{+}\right\rbrace .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8fd60d85fb67797f3d44f5741f97314be2072986)
















![{\displaystyle {\text{ER}}_{g,\beta }(X)=\inf _{t>0,\mu \in \mathbb {R} }\left\lbrace t\left[\mu + {\text{E}}_{P}\left(g^{*}\left({\frac {X}{t}}-\mu +\beta \right)\right)\right]\right\ rbrace }](https://wikimedia.org/api/rest_v1/media/math/render/svg/03980f4d09c2a5a913ca0a64866c3a747d851fd5)




















