Фильтр (имитация больших вихрей)

Фильтрация в контексте моделирования больших вихрей (LES) — это математическая операция, предназначенная для удаления ряда мелких масштабов из решения уравнений Навье-Стокса . Поскольку основная трудность моделирования турбулентных потоков связана с широким диапазоном масштабов длины и времени, эта операция удешевляет моделирование турбулентных потоков за счет сокращения диапазона масштабов, которые необходимо решить. Работа фильтра LES является низкочастотной, то есть он отфильтровывает масштабы, связанные с высокими частотами.

Гомогенные фильтры

Поле скорости, созданное путем прямого численного моделирования (DNS) однородной затухающей турбулентности . Размер домена L ³ .

То же поле скоростей DNS, отфильтрованное с использованием коробчатого фильтра и Δ = L /32.

То же поле скоростей DNS, отфильтрованное с использованием коробчатого фильтра и Δ = L /16.

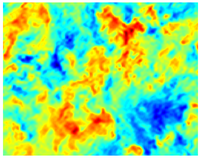
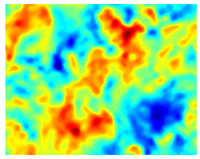
Определение в физическом пространстве

Операция низкочастотной фильтрации, используемая в LES, может применяться к пространственному и временному полю, например $\phi ({\boldsymbol {x}},t)$. Работа фильтра LES может быть пространственной, временной или той и другой. Отфильтрованное поле, обозначенное чертой, определяется как:

${\overline {\phi ({\boldsymbol {x}},t)}}=\displaystyle {\int _{-\infty }^{\infty }}\int _{-\infty }^{\infty }\phi ({\boldsymbol {r}},t^{\prime })G({\boldsymbol {x}}-{\boldsymbol {r}},t-t^{\prime })dt^{\prime }d{\boldsymbol {r}},$

где $G$ — это ядро ​​свертки, уникальное для используемого типа фильтра. Это можно записать как операцию свертки:

${\overline {\phi }}=G\star \phi .$

Ядро фильтра $G$ использует шкалу длины отсечки и времени, обозначенную $\Delta$ и $\tau _{c},$ соответственно. Масштабы меньшие, чем эти, исключаются из ${\overline {\phi }}.$ Используя это определение, любое поле $\phi$ может быть разделен на отфильтрованную и субфильтрованную (обозначенную штрихом) часть, как

$\phi ={\bar {\phi }}+\phi ^{\prime }.$

Это также можно записать как операцию свертки:

$\phi ^{\prime }=\left(1-G\right)\star \phi .$

Определение в спектральном пространстве

Операция фильтрации удаляет масштабы, связанные с высокими частотами, и операцию соответственно можно интерпретировать в пространстве Фурье . Для скалярного поля $\phi ({\boldsymbol {x}},t),$ Фурье преобразование ​ $\phi$ является ${\hat {\phi }}({\boldsymbol {k}},\omega ),$ функция ${\boldsymbol {k}},$ пространственное волновое число и $\omega ,$ временная частота. ${\hat {\phi }}$ можно фильтровать с помощью соответствующего преобразования Фурье ядра фильтра, обозначаемого ${\hat {G}}({\boldsymbol {k}},\omega ):$

${\overline {\hat {\phi }}}({\boldsymbol {k}},\omega )={\hat {\phi }}({\boldsymbol {k}},\omega ){\hat {G}}({\boldsymbol {k}},\omega )$

или,

${\overline {\hat {\phi }}}={\hat {G}}{\hat {\phi }}.$

Ширина фильтра $\Delta$ имеет связанное волновое число среза $k_{c},$ и временная ширина фильтра $\tau _{c}$ также имеет соответствующую частоту среза $\omega _{c}.$ Нефильтрованная часть ${\hat {\phi }}$ является:

${\hat {\phi ^{\prime }}}=(1-{\hat {G}}){\hat {\phi }}.$

Спектральная интерпретация операции фильтрации важна для операции фильтрации при моделировании крупных вихрей, поскольку спектры турбулентных потоков занимают центральное место в моделях подсеточного масштаба LES, которые восстанавливают эффект масштабов подфильтра (самые высокие частоты). Одной из задач подсеточного моделирования является эффективная имитация каскада кинетической энергии от низких частот к высоким. Это делает спектральные свойства реализованного фильтра LES очень важными для моделирования подсеток.

Однородные свойства фильтра

Однородные фильтры LES должны удовлетворять следующему набору свойств при применении к уравнениям Навье-Стокса.

1. Сохранение констант

Значение фильтруемой константы должно быть равно константе,

${\overline {a}}=a,$

что подразумевает,

$\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }G({\boldsymbol {\xi }},t^{\prime })d^{3}{\boldsymbol {\xi }}dt^{\prime }=1.$

2. Линейность

${\overline {\phi +\psi }}={\overline {\phi }}+{\overline {\psi }}.$

3. Коммутация с производными.

${\overline {\frac {\partial \phi }{\partial s}}}={\frac {\partial {\overline {\phi }}}{\partial s}},\qquad s={\boldsymbol {x}},t.$

Если введены обозначения операторной коммутации $[f,g]$ для двух произвольных операторов $f$ и $g$, где

$[f,g]\phi =f\circ g(\phi )-g\circ f(\phi )=f(g(\phi ))-g(f(\phi )),$

то это третье свойство можно выразить как

$\left[G\star ,{\frac {\partial }{\partial s}}\right]=0.$

Фильтры, удовлетворяющие этим свойствам, обычно не являются операторами Рейнольдса , что означает, во-первых:

${\begin{array}{rcl}{\overline {\overline {\phi }}}&\neq &{\overline {\phi }},\\G\star G\star \phi =G^{2}\star \phi &\neq &G\star \phi ,\end{array}}$

и во-вторых,

${\overline {\phi ^{\prime }}}=G\star (1-G)\star \phi \neq 0.$

Неоднородные фильтры

Реализации операций фильтрации для всех потоков, кроме простейших, являются неоднородными операциями фильтрации. Это означает, что поток либо имеет непериодические границы, что вызывает проблемы с фильтрами определенных типов, либо имеет непостоянную ширину фильтра. $\Delta$или и то, и другое. Это предотвращает коммутацию фильтра с производными, а операция коммутации приводит к нескольким дополнительным погрешностям:

${\begin{array}{rcl}\left[{\frac {\partial }{\partial {\boldsymbol {x}}}},G\star \right]\phi &=&{\frac {\partial }{\partial {\boldsymbol {x}}}}\left(G\star \phi \right)-G\star {\frac {\partial \phi }{\partial {\boldsymbol {x}}}}\\&=&{\frac {\partial }{\partial {\boldsymbol {x}}}}\int _{\Omega }G({\boldsymbol {x}}-{\boldsymbol {r}},\Delta ({\boldsymbol {x}},t))\phi ({\boldsymbol {r}},t)d{\boldsymbol {r}}-G\star {\frac {\partial \phi }{\partial {\boldsymbol {x}}}}\\&=&\left({\frac {\partial G}{\partial \Delta }}\star \phi \right){\frac {\partial \Delta }{\partial x}}+\int _{d\Omega }G(x-r,\Delta (x,t))\phi (r,t){\boldsymbol {n}}dS\end{array}},$

где ${\boldsymbol {n}}$ – вектор нормали к поверхности границы $\Omega$ и $d\Omega .$

Оба члена появляются из-за неоднородностей. Первое связано с пространственным изменением размера фильтра. $\Delta ,$ а второе связано с границей домена. Аналогично коммутация фильтра $G$ с производной по времени приводит к ошибке, возникающей из-за временного изменения размера фильтра,

$\left[{\frac {\partial }{\partial t}},G\star \right]=\left({\frac {\partial G}{\partial \Delta }}\star \phi \right){\frac {\partial \Delta }{\partial t}}.$

Было предложено несколько операций фильтрации, которые устраняют или минимизируют эти ошибки.

Классические фильтры для моделирования больших вихрей

Турбулентный энергетический спектр и влияние операций фильтрации

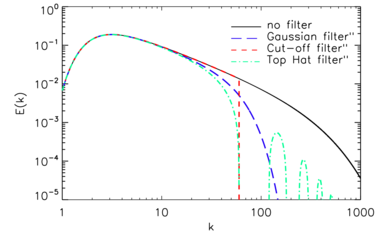
Для пространственной фильтрации при моделировании больших вихрей обычно используются три фильтра. Определение $G({\boldsymbol {x}},t)$ и ${\hat {G}}({\boldsymbol {k}},\omega ),$ и обсуждение важных свойств.

Коробчатый фильтр

Коробчатый фильтр в физическом и спектральном пространстве

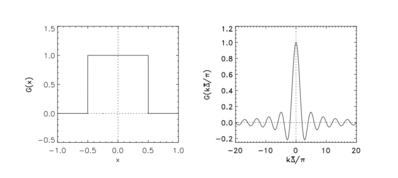
Ядро фильтра в физическом пространстве определяется следующим образом:

$G({\boldsymbol {x}}-{\boldsymbol {r}})={\begin{cases}{\frac {1}{\Delta }},&{\text{if}}\left|{\boldsymbol {x}}-{\boldsymbol {r}}\right|\leq {\frac {\Delta }{2}},\\0,&{\text{otherwise}}.\end{cases}}$

Ядро фильтра в спектральном пространстве определяется формулой:

${\hat {G}}({\boldsymbol {k}})={\frac {\sin {({\frac {1}{2}}k\Delta )}}{{\frac {1}{2}}k\Delta }}.$

Фильтр Гаусса в физическом и спектральном пространстве

Гауссов фильтр

Ядро фильтра в физическом пространстве определяется следующим образом:

$G({\boldsymbol {x}}-{\boldsymbol {r}})=\left({\frac {6}{\pi \Delta ^{2}}}\right)^{\frac {1}{2}}\exp {\left(-{\frac {6({\boldsymbol {x-r}})^{2}}{\Delta ^{2}}}\right)}.$

Ядро фильтра в спектральном пространстве определяется формулой:

${\hat {G}}({\boldsymbol {k}})=\exp {\left(-{\frac {{\boldsymbol {k}}^{2}\Delta ^{2}}{24}}\right)}.$

Резкий спектральный фильтр в физическом и спектральном пространстве

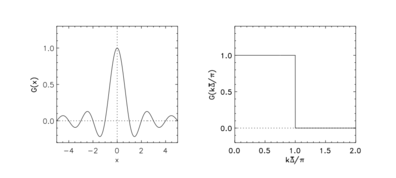
Острый спектральный фильтр

Ядро фильтра в физическом пространстве определяется следующим образом:

$G({\boldsymbol {x}}-{\boldsymbol {r}})={\frac {\sin {(\pi ({\boldsymbol {x-r}})/\Delta )}}{\pi ({\boldsymbol {x-r}})}}.$

Ядро фильтра в спектральном пространстве определяется формулой:

${\hat {G}}({\boldsymbol {k}})=H\left(k_{c}-\left|k\right|\right),\qquad k_{c}={\frac {\pi }{\Delta }}.$

См. также

• Вычислительная гидродинамика
• Фильтр (обработка сигнала)
• Гидравлическая механика
• Преобразование Фурье
• Частотная область
• Моделирование больших вихрей
• Турбулентность