Закон Тициуса – Боде

Закон Тициуса -Боде (иногда называемый просто законом Боде ) представляет собой шаблонное предсказание расстояния между планетами в любой данной планетарной системе . Формула предполагает, что, простираясь наружу, каждая планета должна находиться примерно в два раза дальше от Солнца, чем предыдущая. Гипотеза правильно предсказала орбиты Цереры (в поясе астероидов ) и Урана , но не смогла предсказать орбиту Нептуна . Он назван в честь Иоганна Даниэля Титиуса и Иоганна Элерта Боде .

Более поздние работы Блэгга и Ричардсона существенно пересмотрели исходную формулу и сделали предсказания, которые впоследствии были подтверждены новыми открытиями и наблюдениями. Именно эти переформулировки предлагают «лучшие феноменологические представления расстояний, с помощью которых можно исследовать теоретическое значение законов типа Тициуса-Боде».

Оригинальная формула

Закон связывает большую полуось $~a_{n}~$ Земли каждой планеты наружу от Солнца в таких единицах, что большая полуось равна 10:

$~a=4+x~$

где $~x=0,3,6,12,24,48,96,192,384,768\ldots ~$ так, что, за исключением первого шага, каждое значение в два раза превышает предыдущее. Существует еще одно представление формулы:

$~a=4+3\times 2^{n}~$

где $~n=-\infty ,0,1,2,\ldots ~.$ Полученные значения можно разделить на 10, чтобы преобразовать их в астрономические единицы ( AU ), в результате чего получится выражение:

$a=0.4+0.3\times 2^{n}~.$

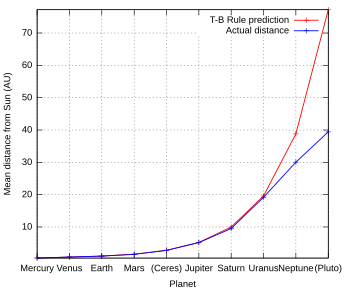
По прогнозам , для дальних внешних планет, за пределами Сатурна , каждая планета будет примерно в два раза дальше от Солнца, чем предыдущий объект. В то время как закон Тициуса-Боде предсказывает, что Сатурн , Уран , Нептун и Плутон находятся примерно в 10, 20, 39 и 77 , фактические значения ближе к 10, 19, 30, 40 а.е. а.е.

Происхождение и история

Иоганн Даниэль Титиус (1729–1796)

Иоганн Элерт Боде (1747–1826)

Первое упоминание о ряде, аппроксимирующем закон Боде, встречается в учебнике Д. Грегори (1715 г.):

«... предположим, что расстояние от Земли до Солнца разделено на десять равных частей, из них расстояние до Меркурия будет около четырех, до Венеры - семь, до Марса - пятнадцать, до Юпитера - пятьдесят две, а до Сатурна - девяносто. пять."

Похожее предложение, вероятно, перефразированное из Григория (1715 г.): появляется в работе, опубликованной К. Вольфом в 1724 году.

В 1764 г. К. Бонне писал:

«Мы знаем семнадцать планет [то есть больших планет и их спутников], входящих в состав нашей Солнечной системы; но мы не уверены, что их больше нет».

В своем переводе работы Бонне в 1766 году Дж. Д. Титиус добавил к приведенному выше заявлению два собственных абзаца. Вставки были помещены внизу страницы 7 и вверху страницы 8. Нового абзаца нет ни в оригинальном французском тексте Бонне, ни в переводах работы на итальянский и английский языки.

Вставленный Тицием текст состоит из двух частей. Первая часть объясняет последовательность расстояний планет от Солнца:

Обратите внимание на расстояния планет друг от друга и признайте, что почти все они отделены друг от друга в пропорции, соответствующей их телесным величинам. Разделите расстояние от Солнца до Сатурна на 100 частей; тогда Меркурий отделен от Солнца на четыре такие части, Венеру на 4+3=7 таких частей, Землю на 4+6=10, Марс на 4+12=16. Но заметьте, что от Марса к Юпитеру происходит отклонение от этой столь точной прогрессии. От Марса следует пространство из 4+24=28 таких частей, но пока там не было обнаружено ни одной планеты. Но следовало ли лорду-архитектору оставить это место пустым? Нисколько. Предположим поэтому, что это пространство без сомнения принадлежит еще неоткрытым спутникам Марса, добавим еще, что, возможно, у Юпитера еще есть вокруг себя какие-то более мелкие спутники, еще не обнаруженные ни одним телескопом. Рядом с этим для нас еще неизведанным пространством возвышается сфера влияния Юпитера в 4+48=52 частях; и у Сатурна в 4+96=100 частей.

В 1772 году Дж. Э. Боде , которому тогда было двадцать пять лет, опубликовал астрономический сборник: в который он включил следующую сноску со ссылкой на Тиция (в более поздних изданиях):

Этот последний пункт, по-видимому, в частности, следует из удивительного соотношения, которое известные шесть планет наблюдают в своих расстояниях от Солнца. Пусть расстояние от Солнца до Сатурна примем за 100, тогда Меркурий отстоят от Солнца на 4 таких части. Венера — 4+3=7. Земля 4+6=10. Марс 4+12=16. Теперь в этом столь упорядоченном развитии возникает пробел. За Марсом следует пространство из 4+24=28 частей, в котором еще не была видна ни одна планета. Можно ли поверить, что Основатель Вселенной оставил это пространство пустым? Конечно, нет. Отсюда мы приближаемся к расстоянию Юпитера на 4+48=52 части и, наконец, к расстоянию Сатурна на 4+96=100 частей.

Эти два утверждения, несмотря на все их своеобразное выражение и исходя из радиусов, используемых для орбит, похоже, происходят из античного алгоритма коссиста .

Было обнаружено множество прецедентов, существовавших еще до семнадцатого века. Тициус был учеником немецкого философа К.Ф. фон Вольфа (1679–1754), и вторая часть текста, который Тициус вставил в работу Бонне, находится в книге фон Вольфа (1723). предполагая, что Тиций узнал об этом от него. В литературе двадцатого века о законе Тициуса-Боде авторство приписывают фон Вольфу. Предыдущая версия была написана Д. Грегори (1702 г.), в которой последовательность планетарных расстояний 4, 7, 10, 16, 52 и 100 стала геометрической прогрессией с соотношением 2. Это ближайшая формула Ньютона, которую также цитировал Бенджамин Мартин (1747). и Томас Серда (ок. 1760 г.) за несколько лет до расширенного перевода Титиусом книги Бонне на немецкий язык (1766 г.). В течение следующих двух столетий последующие авторы продолжали представлять свои собственные модифицированные версии, очевидно, не зная о предыдущих работах.

Титиус и Боде надеялись, что закон приведет к открытию новых планет, и действительно, открытие Урана и Цереры , расстояния которых хорошо соответствуют закону, способствовало известности закона. Однако расстояние до Нептуна было очень разным, и действительно, Плутон, который больше не считается планетой, находится на среднем расстоянии, которое примерно соответствует тому, которое закон Тициуса-Боде предсказал для следующей планеты от Урана.

На момент первоначальной публикации закону примерно удовлетворяли все известные тогда планеты – то есть от Меркурия до Сатурна – с промежутком между четвертой и пятой планетами. Викариус (Иоганн Фридрих) Вурм (1787) предложил модифицированную версию закона Тициуса-Боде, которая учитывала известные тогда спутники Юпитера и Сатурна и лучше предсказала расстояние до Меркурия.

Закон Тициуса-Боде считался интересным, но не имеющим большого значения до открытия Урана в 1781 году, которое почти точно вписывается в этот ряд. Основываясь на этом открытии, Боде призвал своих современников искать пятую планету. Церера , самый большой объект в поясе астероидов , был найден в предсказанном Боде положении в 1801 году.

На тот момент закон Боде получил широкое признание, пока в 1846 году Нептун не был обнаружен в месте, не соответствующем закону. Одновременно из-за большого количества обнаруженных в поясе астероидов Церера перестала быть крупной планетой. В 1898 году астроном и логик К.С. Пирс использовал закон Боде как пример ошибочных рассуждений.

Открытие Плутона в 1930 году еще больше запутало проблему: хотя он и не был близок к предсказанному согласно закону Боде положению, он был очень близок к положению, которое закон определил для Нептуна. Последующее открытие пояса Койпера – и в частности объекта Эрида , который более массивен, чем Плутон, но не соответствует закону Боде – еще больше дискредитировало формулу.

Данные

Закон Тициуса-Боде предсказывает, что планеты будут находиться на определенных расстояниях в астрономических единицах , которые можно сравнить с наблюдаемыми данными для планет и двух карликовых планет в Солнечной системе:

Графический график восьми планет, Плутона и Цереры в сравнении с первыми десятью предсказанными расстояниями.

м	к	Расстояние правила T – B (AU)	Планета	Большая полуось (АС)	Отклонение от прогноза 1
$-\infty$	0	0.4	Меркурий	0.39	−3.23%
0	1	0.7	Венера	0.72	+3.33%
1	2	1.0	Земля	1.00	0.00%
2	4	1.6	Марс	1.52	−4.77%
3	8	2.8	Церера 2	2.77	−1.16%
4	16	5.2	Юпитер	5.20	+0.05%
5	32	10.0	Сатурн	9.58	−4.42%
6	64	19.6	Уран	19.22	−1.95%
–	–	–	Нептун	30.07	–
7	128	38.8	Плутон 2	39.48	+1.02%

¹ Для больших k каждое расстояние по правилу Тициуса-Боде примерно в два раза превышает предыдущее значение. Следовательно, произвольную планету можно найти в пределах от -25% до +50% от одного из предсказанных положений. При малых k предсказанные расстояния не удваиваются полностью, поэтому диапазон потенциального отклонения меньше. Обратите внимание, что большая полуось пропорциональна 2/3 степени орбитального периода . Например, планеты в орбитальном резонансе 2:3 (например, плутино относительно Нептуна ) будут различаться по расстоянию на (2/3) ^2/3 = −23,69% и +31,04% относительно друг друга.
² Церера и Плутон — скорее карликовые планеты , чем большие планеты .

Формулировка Блэгга

В 1913 году М. А. Благг , оксфордский астроном, вновь обратился к этому закону. Она проанализировала орбиты планетной системы и спутниковых систем внешних газовых гигантов — Юпитера, Сатурна и Урана. Она изучила журнал расстояний, пытаясь найти лучшую «среднюю» разницу.

Эмпирическая поправочная функция f, введенная в переформулировке Блэгга закона Тициуса – Боде.

Ее анализ привел к другой формуле:

$\ {\mathsf {distance}}=A\cdot {\bigl [}\ B+f\left(\alpha +n\ \beta \right)\ {\bigr ]}\ {\bigl (}\ 1.7275\ {\bigr )}^{n}~.$

Обратите внимание, в частности, что в формуле Благага закон Солнечной системы лучше всего был представлен прогрессией 1,7275 , а не исходным значением 2, используемым Тициусом, Боде и другими.

Благг исследовал спутниковую систему Юпитера , Сатурна и Урана и обнаружил в каждой из них одинаковый коэффициент прогрессии 1,7275 .

Однако окончательная форма поправочной функции f не была указана в статье Благага 1913 года, при этом Благг отметил, что приведенные эмпирические цифры предназначены только для иллюстрации. Эмпирическая форма была представлена ​​в виде графика (причина того, что точки на кривой так близко соответствуют эмпирическим данным для объектов, обнаруженных до 1913 года, заключается в том, что они являются эмпирическими данными).

Найти формулу, которая точно соответствовала бы эмпирической кривой, оказалось непросто. Фурье-анализ формы привел к следующему семичленному приближению:

$${\begin{aligned}\ f{\bigl (}\ \theta \ {\bigr )}\;=\;0.4594\;+\;\;&0.396\ \cos \!{\bigl (}\ \theta -27.4^{\circ }\ {\bigr )}\;+\;0.168\ \cos \!{\bigl (}\ 2\ (\ \theta -60.4^{\circ })\ {\bigr )}\;+\;0.062\ \cos \!{\bigl (}\ 3\ (\ \theta -28.1^{\circ })\ {\bigr )}\;+\;\\\;+\;\;&0.053\ \cos \!{\bigl (}\ 4\ (\ \theta -77.2^{\circ })\ {\bigr )}\;+\;0.009\ \cos \!{\bigl (}\ 5\ (\ \theta -22^{\circ })\ {\bigr )}\;+\;0.012\ \cos \!{\bigl (}\ 7\ (\ \theta -40.4^{\circ })\ {\bigr )}~.\end{aligned}}$$

После дальнейшего анализа Благг дал следующую более простую формулу; однако цена более простой формы заключается в том, что она менее точно соответствует эмпирическим данным. Благг представила его в ненормализованной форме в своей статье, что оставляет относительные размеры A , B и f неоднозначными; здесь он показан в нормализованной форме (т.е. эта версия f масштабируется для получения значений от 0 до 1 включительно):

$$\ f{\bigl (}\ \theta \ {\bigr )}\;=\;0.249\;+\;0.860\ \left({\frac {\ \cos \ \Psi \ }{\ 3-\cos \!\left(\ 2\ \Psi \ \right)\ }}\;+\;{\frac {1}{\ 6-4\ \cos \!\left(\ 2\ \Psi -60^{\circ }\right)\ }}\right)\ ,$$

где $\ \Psi \equiv \theta -27.5^{\circ }~.$

Ни одна из этих формул для функции f не используется в приведенных ниже расчетах: Здесь расчеты основаны на графике функции f , построенном на основе наблюдаемых данных.

Константы для уточнения Благагом закона Тициуса – Боде
(в редакции Ньето, 1970 г. )

Система	А	Б	а	б
Тела, вращающиеся вокруг Солнца	0.4162	2.025 0	112.4°	0 56.6°
Спутники Юпитера	0.4523	1.852 0	113.0°	0 36.0°
Спутники Сатурна	3.074 0	0.0071	118.0°	0 10.0°
Спутники Урана	2.98 0 0	0.0805	125.7°	0 12.5°

Ее статья была опубликована в 1913 году и была забыта до 1953 года, когда А. Э. Рой наткнулся на нее во время исследования другой проблемы. Рой отметил, что сама Благг предположила, что ее формула может дать приблизительные средние расстояния до других тел, еще не открытых в 1913 году. С тех пор было открыто шесть тел в трех системах, исследованных Благгом: Плутон , Синопа ( Юпитер IX ), Лисифея ( J X ). , Карме ( J XI ), Ананке ( J XII ) и Миранда ( Уран V ).

Рой обнаружил, что все шестеро подходят друг другу очень близко. Это могло быть преувеличением: из этих шести тел четыре находились на одной позиции с объектами, которые были известны уже в 1913 году; что касается двух других, то оценка Плутона была завышена примерно на 6%; а позже стала очевидной недооценка Миранды на 6%.

Сравнение формулировки Блага с наблюдением

Тела в скобках не были известны в 1913 году, когда Блэгг писала свою статью. Некоторые из расчетных расстояний в системах Сатурна и Урана не очень точны. Это связано с тем, что низкие значения константы B в таблице выше делают их очень чувствительными к точному виду функции f .

Тела, вращающиеся вокруг Солнца Планета / минор пл. н обс. расст. Благг пред. Меркурий −2 0.387 0.387 Венера −1 0.723 0.723 Земля 0 1.000 1.000 Марс 1 1.524 1.524 Веста 2 2.362 2.67 0 Юнона 2.670 Паллада 2.774 Церера 2.769 Юпитер 3 5.204 5.200 Сатурн 4 9.583 9.550 Уран 5 19.22 0 19.23 0 Нептун 6 30.07 0 30.13 0 (Плутон) 7 (39.48) 41.8 0 0

Спутники Юпитера Спутник Юпитера н обс. расст. Благг пред. Амальтея −2 0.429 0.429 — −1 — 0.708 Этот 0 1.000 1.000 Европа 1 1.592 1.592 Ганимед 2 2.539 2.541 Каллисто 3 4.467 4.467 — 4 — 9.26 0 — 5 — 15.4 0 0 Гималия 6 27.25 0 27.54 0 Элара 27.85 0 ( Лисифея ) (27.85) ( Ананка ) 7 (49.8) 0 55.46 0 ( Кармен ) (53.3) 0 Пасифая 55.7 0 0 ( Синопа ) (56.2) 0

Спутники Сатурна спутник Сатурна н обс. расст. Благг пред. ( Янус ) −3 (0.538) 0.54 0 Мим −2 0.630 0.629 Энцелад −1 0.808 0.807 Тетис 0 1.000 1.000 Диона 1 1.281 1.279 Рея 2 1.789 1.786 — 3 — 2.97 0 Титан 4 4.149 4.140 Гиперион 5 5.034 5.023 — 6 — 6.3 0 0 — 7 — 6.65 0 — 8 — 7.00 0 Япет 9 12.09 0 12.11 0 Фиби 10 43.92 0 43.85 0

Спутники Урана Спутник Урана н обс. расст. Благг пред. ( Миранда ) −2 (0.678) 0.64 0 — −1 — 0.77 0 Ариэль 0 1.000 1.000 Умбриэль 1 1.394 1.393 Титания 2 2.293 2.286 Оберон 3 3.058 3.055

Формулировка Ричардсона

В Popular Astronomy 1945 года статье журнала научный писатель Д.Э. Ричардсон, очевидно, независимо пришел к тому же выводу, что и Благг: коэффициент прогрессии равен 1,728 , а не 2 . Его пространственный закон имеет вид:

$$\ R_{n}={\bigl (}\ 1.728\ {\bigr )}^{n}\ \varrho _{n}(\theta _{n})\ ,$$

где $\varrho _{n}$ представляет собой колебательную функцию с периодом $2\pi$, представляющий расстояния $\varrho _{n}$ от смещенного от центра начала координат к точкам на эллипсе.

Историческая инерция

Ньето, который провел первый современный комплексный обзор закона Тициуса-Боде, отметил, что «Психологическая сила Закона об астрономии была такова, что люди всегда были склонны рассматривать его первоначальную форму как основу для построения теорий». Он подчеркивал, что «будущие теории должны избавиться от предвзятости, пытаясь объяснить коэффициент прогрессии, равный 2»:

Следует подчеркнуть одну вещь: необходимо отказаться от исторического предвзятого отношения к коэффициенту прогрессии, равному 2 . Должно быть ясно, что первую формулировку Тиция (с ее асимметричным первым членом) следует рассматривать как хорошее первое предположение . Конечно, это не обязательно следует рассматривать как лучшее предположение для ссылки на теории. Но в астрономии тяжесть истории тяжела... Несмотря на то, что число 1,73 гораздо лучше, астрономы цепляются за исходное число 2.

Теоретические объяснения

Никакого твердого теоретического объяснения не лежит в основе закона Тициуса-Боде, но возможно, что, учитывая сочетание орбитального резонанса и нехватки степеней свободы , любая стабильная планетная система с высокой вероятностью будет удовлетворять соотношению типа Тициуса-Боде. Поскольку это может быть математическое совпадение, а не «закон природы», его иногда называют правилом, а не «законом». Астрофизик Алан Босс утверждает, что это просто совпадение, и планетологический журнал « Икар» больше не принимает статьи, пытающиеся предоставить улучшенные версии «закона».

Орбитальный резонанс крупных орбитальных тел создает области вокруг Солнца , свободные от долговременных стабильных орбит. Результаты моделирования формирования планет подтверждают идею о том, что случайно выбранная стабильная планетная система, вероятно, будет удовлетворять закону Тициуса-Боде.

Дюбрюль и Гранер показал, что степенные правила расстояний могут быть следствием моделей коллапсирующих облаков планетных систем, обладающих двумя симметриями: вращательной инвариантностью (т. е. облако и его содержимое осесимметричны) и масштабной инвариантностью (т. е. облако и его содержимое выглядят как одинаково во всех масштабах). Последнее является особенностью многих явлений, которые, как считается, играют роль в формировании планет, таких как турбулентность.

Естественные спутниковые системы и экзопланетные системы

В настоящее время доступно лишь ограниченное количество систем, на которых можно проверить закон Боде; две солнечные планеты имеют достаточно большие спутники, которые, вероятно, образовались в процессе, подобном тому, который сформировал планеты: четыре больших спутника Юпитера и самый большой внутренний спутник (т. е. Амальтея ) цепляются за регулярное, но не Тициуса-Боде, расстояние , при этом четыре самых внутренних спутника привязаны к орбитальным периодам, каждый из которых в два раза больше, чем у следующего внутреннего спутника. Точно так же большие спутники Урана имеют регулярное расстояние, но не Тициуса-Боде. Однако, по словам Мартина Харвита

«Небольшая новая формулировка этого закона позволяет нам включать не только орбиты планет вокруг Солнца, но и орбиты лун вокруг их родительских планет».

Новая формулировка известна как « закон Дермотта ».

Из недавних открытий внесолнечных планетных систем лишь немногие имеют достаточно известных планет, чтобы проверить, применимы ли подобные правила. Попытка с 55 Cancri привела к уравнению

$~a_{n}=0.0142\cdot \mathrm {e} ^{\left(\,0.9975\,n\,\right)}=0.0142\cdot {\bigl (}\,2.7115\,{\bigr )}^{n}~,$

и спорно предсказывает неоткрытую планету или астероидное поле для $~n=5~$ в 2 АС . Кроме того, орбитальный период и большая полуось самой внутренней планеты в системе 55 Раков были значительно пересмотрены (с 2,817 дней до 0,737 дней и с 0,038 до 0,016 а.е. соответственно). с момента публикации этих исследований

Недавние астрономические исследования показывают, что планетные системы вокруг некоторых других звезд могут подчиняться законам Тициуса-Боде. Бовэр и Лайнвивер (2013) применил обобщенное соотношение Тициуса-Боде к 68 экзопланетным системам, содержащим четыре или более планет. Они показали, что 96% этих экзопланетных систем придерживаются обобщенного соотношения Тициуса-Боде в такой же или большей степени, чем Солнечная система. В каждой системе прогнозируется местоположение потенциально необнаруженных экзопланет.

Последующие исследования обнаружили 5 планет-кандидатов из 97 планет, предсказанных для 68 планетных систем. Исследование показало, что реальное количество планет может быть больше. Частота появления планет размером с Марс и Меркурий в настоящее время неизвестна, поэтому многие планеты могут быть пропущены из-за их небольшого размера. Другие возможные причины, которые могут объяснить очевидные расхождения, включают планеты, которые не проходят транзитом мимо звезды, или обстоятельства, при которых предсказанное пространство занято околозвездными дисками . Несмотря на такие допущения, количество планет, обнаруженных с помощью предсказаний закона Тициуса – Боде, было ниже, чем ожидалось.

В статье 2018 года идея гипотетической восьмой планеты вокруг TRAPPIST-1 под названием «TRAPPIST-1i» была предложена с использованием закона Тициуса-Боде. TRAPPIST-1i сделал прогноз, основанный исключительно на законе Тициуса-Боде с орбитальным периодом 27,53 ± 0,83 дня .

Наконец, необработанные статистические данные экзопланетных орбит убедительно указывают на общее выполнение законов типа Тициуса-Боде (с экспоненциальным увеличением больших полуосей в зависимости от планетарного индекса) во всех экзопланетных системах; при составлении слепой гистограммы больших полуосей орбит для всех известных экзопланет, для которых известна эта величина, и сравнении ее с тем, что следует ожидать, если планеты распределятся по законам типа Тициуса-Боде, наблюдается значительная степень согласия (т.е. , 78%) получается.

См. также

• Закон Дермотта
• Фаэтон (гипотетическая планета)
• Логарифмическая спираль
• Потенциал Леннарда-Джонса
• Космографическая тайна

Дальнейшее чтение

• Мэтьюз, Роберт (9 апреля 1994 г.). «Призрачная рука, раскинувшая планеты» . Новый учёный . п. 13.
• Пердейк, HJR «Объяснение закона Тициуса-Боде» . Растения и планеты. Архивировано из оригинала 15 июля 2014 года . Проверено 26 января 2024 г. - через kpn.nl. {{cite web}}:CS1 maint: unfit URL ( ссылка ) — мистический и умозрительный; исх. схемы отсутствуют в архиве
• Парес и Фаррас, Рамон, доктор. (2016). Планетарные расстояния и закон Тициуса-Боде (PDF) (популярное эссе по астрономии) (на испанском языке) . Проверено 26 января 2024 г. - через wix.com. {{cite report}}: CS1 maint: несколько имен: список авторов ( ссылка ) — сочетание истории измерений расстояний и развития закона Тициуса, участие известных астрономов, а также изложение графиков и простых соотношений современных планетных и спутниковых расстояний.