Теорема о проекционном срезе

Теорема Фурье о срезе

В математике , теорема о проекционном срезе теорема о центральном срезе или теорема о срезе Фурье в двух измерениях утверждает, что результаты следующих двух вычислений равны:

• Возьмите двумерную функцию f ( r ), спроецируйте ее (например, с помощью преобразования Радона ) на (одномерную) линию и выполните преобразование Фурье этой проекции.
• Возьмите ту же функцию, но сначала выполните двумерное преобразование Фурье, а затем разрежьте ее по началу координат, параллельному линии проекции.

С точки зрения оператора, если

• F ₁ и F ₂ — упомянутые выше 1- и 2-мерные операторы преобразования Фурье,
• P ₁ — оператор проецирования (который проецирует двумерную функцию на одномерную линию),
• S ₁ — оператор среза (который извлекает одномерный центральный срез из функции),

затем

$F_{1}P_{1}=S_{1}F_{2}.$

Эту идею можно распространить на более высокие измерения.

Эта теорема используется, например, при анализе медицинских КТ , где «проекция» представляет собой рентгеновский снимок.изображение внутреннего органа. Преобразования Фурье этих изображений:рассматриваются как срезы преобразования Фурье трехмерногоплотность внутреннего органа, и эти срезы можно интерполировать для построенияполное преобразование Фурье этой плотности. Обратное преобразование Фурьезатем используется для восстановления трехмерной плотности объекта. Этот метод был впервые разработан Рональдом Н. Брейсуэллом в 1956 году для решения радиоастрономических задач.

Теорема о проекционном срезе в N измерениях

В N измерениях теорема о проекционном срезе утверждает, что Преобразование Фурье проекции N -мерной функции f ( r ) на m -мерное линейное подмногообразие равен m -мерному срезу N -мерного преобразования Фурье этогофункция, состоящая из m -мерного линейного подмногообразия, проходящего через начало координат в пространстве Фурье, параллельного проекционному подмногообразию. В терминах оператора:

$F_{m}P_{m}=S_{m}F_{N}.\,$

Обобщенная теорема о срезах Фурье

Помимо обобщения на N измерений, теорема о проекционном срезе может быть дополнительно обобщена с произвольной заменой базиса. Для удобства обозначений мы считаем, что изменение базиса должно быть представлено как B , N на обратимая матрица размера N, работающая с N -мерными векторами-столбцами. Тогда обобщенную теорему Фурье о срезах можно сформулировать как

$F_{m}P_{m}B=S_{m}{\frac {B^{-T}}{|B^{-T}|}}F_{N}$

где $B^{-T}=(B^{-1})^{T}$ является транспонированием обратного преобразования изменения базиса.

Доказательство в двух измерениях

Графическая иллюстрация теоремы о проекционном срезе в двух измерениях. f ( r ) и F ( k ) — пары двумерных преобразований Фурье. Проекция f ( r ) на ось x представляет собой интеграл f ( r ) вдоль линий взгляда, параллельных оси y , и обозначается p ( x ). Срез через F ( k ) находится на оси k _x , которая параллельна оси x и обозначена s ( k _x ). Теорема о проекционном срезе утверждает, что p ( x ) и s ( k _x ) являются одномерными парами преобразований Фурье.

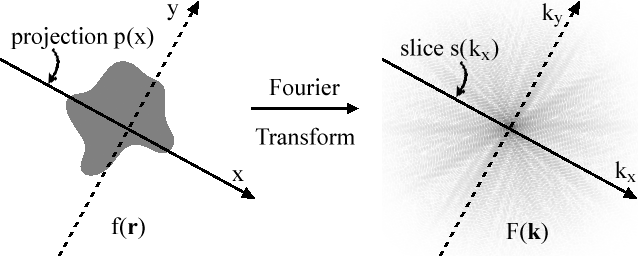
Теорема о проекционном срезе легко доказывается для случая двух измерений.Без ограничения общности мы можем принять линию проекции за ось x .При этом нет потери общности, поскольку если мы используем сдвинутую и повернутую линию, закон по-прежнему применяется. Использование смещенной линии (по оси y) дает ту же проекцию и, следовательно, те же результаты одномерного преобразования Фурье. Повернутая функция — это пара Фурье повернутого преобразования Фурье, для которой теорема снова справедлива.

Если f ( x , y ) двумерная функция, то проекция f ( x , y ) на ось x равна p ( x ), где

$p(x)=\int _{-\infty }^{\infty }f(x,y)\,dy.$

Преобразование Фурье $f(x,y)$ является

$F(k_{x},k_{y})=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }f(x,y)\,e^{-2\pi i(xk_{x}+yk_{y})}\,dxdy.$

Затем кусок $s(k_{x})$

$s(k_{x})=F(k_{x},0)=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }f(x,y)\,e^{-2\pi ixk_{x}}\,dxdy$

$=\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }f(x,y)\,dy\right]\,e^{-2\pi ixk_{x}}dx$

$=\int _{-\infty }^{\infty }p(x)\,e^{-2\pi ixk_{x}}dx$

что является всего лишь преобразованием Фурье p ( x ). Доказательство для более высоких размерностей легко обобщается из приведенного выше примера.

Цикл ФГА

Если двумерная функция f ( r ) кругосимметрична, ее можно представить как f ( r ), где r = | р |. В этом случае проекция на любую проекционную прямуюбудет Абеля преобразованием f ( r ). Двумерное преобразование Фурье f r ( r нулевого порядка заданной преобразованием Ханкеля f ), которое , ( ) будет кругово-симметричной функцией , следовательно, также будет представлять любой срез, проходящий через начало координат. Теорема о срезе проекции затем утверждает, что преобразование Фурье проекции равно срезу или

$F_{1}A_{1}=H,$

где A ₁ представляет оператор преобразования Абеля, проецирующий двумерную кругово-симметричную функцию на одномерную линию, F ₁ представляет собой 1-D преобразование Фурьеоператор, а H представляет оператор преобразования Ханкеля нулевого порядка.

Расширение для веерного или конусного КТ

Теорема о срезах проекций подходит для реконструкции КТ-изображений с использованием параллельных проекций лучей. Это не применимо напрямую к веерной или конусной КТ. Теорема была распространена на реконструкцию веерных и конусных компьютерных изображений Шуан-жэнь Чжао в 1995 году.

См. также

• Преобразование Радона § Связь с преобразованием Фурье

Дальнейшее чтение

• Брейсвелл, Рональд Н. (1990). «Численные преобразования». Наука . 248 (4956): 697–704. Бибкод : 1990Sci...248..697B . дои : 10.1126/science.248.4956.697 . ПМИД   17812072 . S2CID   5643835 .
• Брейсвелл, Рональд Н. (1956). «Полосовая интеграция в радиоастрономии» . Ауст. Дж. Физ . 9 (2): 198. Бибкод : 1956AuJPh...9..198B . дои : 10.1071/PH560198 .
• Гаскилл, Джек Д. (2005). Линейные системы, преобразования Фурье и оптика . Джон Уайли и сыновья, Нью-Йорк. ISBN  978-0-471-29288-3 .
• Нг, Рен (2005). «Фотография среза Фурье» (PDF) . Транзакции ACM с графикой . 24 (3): 735–744. дои : 10.1145/1073204.1073256 .
• Чжао, Шуан-Рэнь; Холлинг, Хорст (1995). «Реконструкция проекций конусного луча со свободным путем источника с помощью обобщенного метода Фурье». Материалы Международного совещания 1995 г. по полной реконструкции трехмерных изображений в радиологии и ядерной медицине : 323–7.
• Гарсес, Дэйзи Х.; Роудс, Уильям Т.; Пенья, Нестор (2011). «Теорема о проекционном срезе: компактная запись». Журнал Оптического общества Америки А. 28 (5): 766–769. Бибкод : 2011JOSAA..28..766G . дои : 10.1364/JOSAA.28.000766 . ПМИД   21532686 .

Внешние ссылки

• Теорема Фурье о срезах (видео). Часть курса «Компьютерная томография и набор инструментов ASTRA». Университет Антверпена . 10 сентября 2015 г.