Додекаэдрическая призма
| Додекаэдрическая призма | |
|---|---|
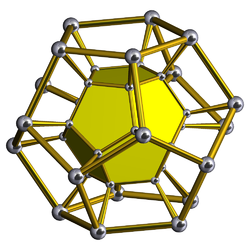 Диаграмма Шлегеля Показана только одна додекаэдрическая ячейка | |
| Тип | Призматический однородный 4-многогранник |
| Единый индекс | 57 |
| Символ Шлефли | t{2,5,3} или {5,3}×{} |
| Коксетер-Дынкин | |
| Клетки | 2 ( 5.5.5 ) 12 ( 4.4.5 ) |
| Лица | 30 {4} 24 {5} |
| Края | 80 |
| Вершины | 40 |
| Вершинная фигура | 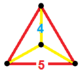 Равносторонне-треугольная пирамида |
| Двойной | Икосаэдрическая бипирамида |
| Группа симметрии | [5,3,2], порядок 240 |
| Характеристики | выпуклый |

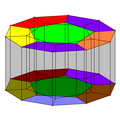
В геометрии — додекаэдральная призма это выпуклый однородный 4-многогранник . Этот 4-многогранник имеет 14 многогранных ячеек: 2 додекаэдра, соединенных 12 пятиугольными призмами . У него 54 грани: 30 квадратов и 24 пятиугольника. Он имеет 80 ребер и 40 вершин.
Его можно построить, создав два совпадающих додекаэдра в трехмерном пространстве и переместив каждую копию в противоположных перпендикулярных направлениях в четырехмерном пространстве до тех пор, пока их расстояние не станет равным длине их ребра.
Это одна из 18 выпуклых однородных многогранных призм, созданных с помощью однородных призм для соединения пар параллельных платоновых тел или архимедовых тел .
Альтернативные названия
[ редактировать ]- Додекаэдрическая диадическая призма Нормана В. Джонсона
- Додекаэдрическая гиперпризма
Изображения
[ редактировать ]- Прозрачная диаграмма Шлегеля .
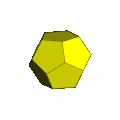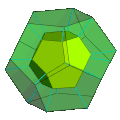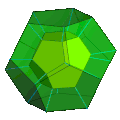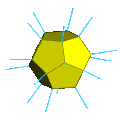
- Орфографическая проекция с каркасной моделью, в которой половина пятиугольных граней окрашена так, чтобы показать два додекаэдра. Додекаэдры правильные, но кажутся сплюснутыми из-за проекции и направления взгляда.
- Каркасная перспективная проекция двойной вращающейся додекаэдрической призмы.
Структура
[ редактировать ]Додекаэдрическая призма состоит из двух додекаэдров, соединенных друг с другом 12 пятиугольными призмами. Пятиугольные призмы соединены друг с другом квадратными гранями.
Прогнозы
[ редактировать ]Орфографическая проекция додекаэдральной призмы в трехмерное пространство, основанная на пятиугольной призме, имеет десятиугольную оболочку (см. Диаграмму). Две пятиугольные призмы выступают в центр этого объема, каждая из которых окружена пятью другими пятиугольными призмами. Они образуют два набора (каждый из которых состоит из центральной пятиугольной призмы, окруженной пятью другими неоднородными пятиугольными призмами), которые дважды покрывают объем десятиугольной призмы. Два додекаэдра выступают на десятиугольные грани оболочки.
Орфографическая проекция додекаэдрической призмы в трехмерное пространство, начиная с додекаэдра, имеет додекаэдрическую оболочку. Две додекаэдрические ячейки проецируются на весь объем этой оболочки, а 12 десятиугольных призматических ячеек проецируются на ее 12 пятиугольных граней.
Внешние ссылки
[ редактировать ]- 6. Выпуклая равномерно-призматическая полихора — Модель 57 , Георгий Ольшевский.
- Клитцинг, Ричард. «4D однородные многогранники (полихора) x o3o5x — допинг» .