Теорема об углах
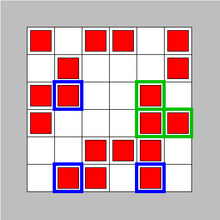
В арифметической комбинаторике теорема об углах утверждает, что для каждого , для достаточно большого , любой набор по крайней мере точки в сетка содержит угол, т. е. тройку точек вида с . Впервые это было доказано Миклошем Айтаи и Эндре Семереди в 1974 году с использованием теоремы Семереди . [1] В 2003 году Йожеф Солимоши дал краткое доказательство, используя лемму об удалении треугольника . [2]
Заявление
[ редактировать ]Определите угол как подмножество формы , где и . Для каждого , существует целое положительное число такой, что для любого , любое подмножество хотя бы с размером содержит угол.
Состояние можно расслабиться, чтобы показав, что если плотно, то оно имеет некоторое плотное подмножество, центрально симметричное.
Обзор доказательств
[ редактировать ]Далее следует краткий обзор аргументации Солимоси.
Предполагать без углов. Построить вспомогательный трехдольный граф с частями , , и , где соответствует строке , соответствует строке , и соответствует строке . Соедините две вершины, если пересечение соответствующих им прямых лежит в .
Обратите внимание, что треугольник в соответствует углу в , за исключением тривиального случая, когда линии, соответствующие вершинам треугольника, совпадают в точке . Отсюда следует, что каждое ребро находится ровно в одном треугольнике, поэтому по лемме об удалении треугольника , имеет края, так что , по желанию.
Количественные границы
[ редактировать ]Позволять быть размером наибольшего подмножества который не содержит углов. Наиболее известные границы:
где и . Нижняя оценка принадлежит Грину, [3] опираясь на работы Линиала и Шрайбмана. [4] Верхняя оценка принадлежит Шкредову. [5]
Многомерное расширение
[ редактировать ]Уголок в представляет собой множество точек вида , где является стандартной основой , и . Естественное распространение теоремы об углах на этот случай можно показать с помощью леммы об удалении гиперграфа в духе доказательства Солимози. Лемма об удалении гиперграфа была независимо доказана Гауэрсом. [6] и Нэгле, Рёдль, Шахт и Скокан. [7]
Многомерная теорема Семереди.
[ редактировать ]Многомерная теорема Семереди утверждает, что для любого фиксированного конечного подмножества , и для каждого , существует целое положительное число такой, что для любого , любое подмножество хотя бы с размером содержит подмножество формы . Эта теорема следует из теоремы о многомерных углах с помощью простого проекционного аргумента. [6] В частности, теорема Рота об арифметических прогрессиях непосредственно следует из теоремы об обычных углах.
Ссылки
[ редактировать ]- ^ Айтаи, Миклош ; Семереди, Эндре (1974). «Наборы точек решетки, не образующие квадратов». Стад. Наука. Венгерский . 9 : 9–11. МР 0369299 . .
- ^ Солимоси, Йожеф (2003). «Заметка об обобщении теоремы Рота». В Аронов Борис; Басу, Саугата; Пах, Янош; и др. (ред.). Дискретная и вычислительная геометрия . Алгоритмы и комбинаторика. Том. 25. Берлин: Шпрингер-Верлаг. стр. 825–827. дои : 10.1007/978-3-642-55566-4_39 . ISBN 3-540-00371-1 . МР 2038505 .
- ^ Грин, Бен (2021). «Нижние границы для наборов без углов». Новозеландский математический журнал . 51 . arXiv : 2102.11702 . дои : 10.53733/86 .
- ^ Линиал, Нати ; Шрайбман, Ади (2021). «Большие наборы без углов из лучших протоколов NOF Exactly-N». Дискретный анализ . 2021 . arXiv : 2102.00421 . дои : 10.19086/da.28933 . S2CID 231740736 .
- ^ Шкредов И.Д. (2006). «Об одном обобщении теоремы Семереди». Труды Лондонского математического общества . 93 (3): 723–760. arXiv : math/0503639 . дои : 10.1017/S0024611506015991 . S2CID 55252774 .
- ^ Jump up to: Перейти обратно: а б Гауэрс, Тимоти (2007). «Регулярность гиперграфа и многомерная теорема Семереди». Анналы математики . 166 (3): 897–946. arXiv : 0710.3032 . дои : 10.4007/анналы.2007.166.897 . МР 2373376 . S2CID 56118006 .
- ^ Родл, В.; Нэгл, Б.; Скокан, Дж.; Шахт, М.; Кохаякава, Ю. (26 мая 2005 г.). «С обложки: метод регулярности гиперграфа и его приложения» . Труды Национальной академии наук . 102 (23): 8109–8113. Бибкод : 2005PNAS..102.8109R . дои : 10.1073/pnas.0502771102 . ISSN 0027-8424 . ПМЦ 1149431 . ПМИД 15919821 .
Внешние ссылки
[ редактировать ]- Доказательство теоремы об углах в эрудитах.




























![{\displaystyle [N]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a3fc0eabf5a5f3e92ccb827592993f644b662a3)












