Метод информационного узкого места

Метод информационного узкого места — это метод теории информации, предложенный Нафтали Тишби , Фернандо К. Перейрой и Уильямом Биалеком . Он предназначен для поиска наилучшего компромисса между точностью и сложностью ( сжатием ) при суммировании (например, кластеризации ) случайной величины X с учетом совместного распределения вероятностей p(X,Y) между X и наблюдаемой соответствующей переменной Y - и самоописываемого как предоставление «удивительно богатой основы для обсуждения множества проблем обработки и обучения сигналов» .

Приложения включают распределенную кластеризацию и уменьшение размерностей , а в последнее время это было предложено в качестве теоретической основы для глубокого обучения . Он обобщил классическое понятие минимальной достаточной статистики с параметрической статистики на произвольные распределения, не обязательно экспоненциальной формы. Это достигается за счет ослабления условия достаточности для захвата некоторой доли взаимной информации с помощью соответствующей переменной Y .

Информационное узкое место также можно рассматривать как проблему искажения скорости с функцией искажения, которая измеряет, насколько хорошо Y прогнозируется на основе сжатого представления T по сравнению с его прямым прогнозированием на основе X . Эта интерпретация обеспечивает общий итерационный алгоритм для решения проблемы информационного узкого места и расчета информационной кривой на основе распределения p(X,Y) .

Пусть сжатое представление задается случайной величиной $T$. Алгоритм минимизирует следующий функционал относительно условного распределения $p(t|x)$:

$\inf _{p(t|x)}\,\,{\Big (}I(X;T)-\beta I(T;Y){\Big )},$

где $I(X;T)$ и $I(T;Y)$ являются взаимной информацией $X$ и $T$и из $T$ и $Y$соответственно и $\beta$ является множителем Лагранжа .

Теория обучения для глубокого обучения

Математически доказано, что контроль узких мест в информации является одним из способов контроля ошибок обобщения в глубоком обучении. А именно, доказано, что ошибка обобщения масштабируется как ${\tilde {O}}\left({\sqrt {\frac {I(X,T)+1}{n}}}\right)$ где $n$ количество обучающих выборок, $X$ является входными данными для глубокой нейронной сети, а $T$ это результат скрытого слоя. Это обобщение связано со степенью узкого места в информации, в отличие от других границ обобщения, которые масштабируются с количеством параметров, размерностью VC , сложностью Радемахера , стабильностью или надежностью.

Информационная теория глубокого обучения

Теория информационных узких мест недавно использовалась для изучения глубоких нейронных сетей (DNN). Учитывать $X$ и $Y$ соответственно как входной и выходной слои DNN, и пусть $T$ быть любым скрытым слоем сети. Шварц-Зив и Тишби предложили информационное узкое место, которое отражает компромисс между мерами взаимного информирования. $I(X,T)$ и $I(T,Y)$. В этом случае, $I(X,T)$ и $I(T,Y)$ соответственно количественно оценить объем информации, которую содержит скрытый слой о входных и выходных данных.Они предположили, что процесс обучения DNN состоит из двух отдельных этапов; 1) начальная фаза подгонки, на которой $I(T,Y)$ увеличивается, и 2) последующая фаза сжатия, в которой $I(X,T)$ уменьшается. Сакс и др. в опроверг иск Шварц-Зива и Тишби, заявив, что это явление сжатия в DNN не является всеобъемлющим и зависит от конкретной функции активации. В частности, они утверждали, что при использовании функций активации ReLu сжатие не происходит. Шварц-Зив и Тишби оспорили эти утверждения, утверждая, что Сакс и др. не наблюдал сжатия из-за слабых оценок взаимной информации. Недавно Ношад и др. использовал оптимальную по скорости оценку взаимной информации, чтобы исследовать это противоречие, отметив, что оптимальная оценка на основе хэша выявляет явление сжатия в более широком диапазоне сетей с активациями ReLu и maxpooling. С другой стороны, недавно Goldfeld et al. утверждали, что наблюдаемое сжатие является результатом геометрических, а не теоретико-информационных явлений. точка зрения, которая была распространена также в.

Гауссово узкое место

Гауссово узкое место, а именно, применение подхода к информационным узким местам к гауссовским переменным приводит к решениям, связанным с каноническим корреляционным анализом. Предполагать $X,Y\,$ являются совместно многомерными нормальными векторами с нулевым средним значением с ковариациями $\Sigma _{XX},\,\,\Sigma _{YY}$ и $T\,$ представляет собой сжатую версию $X\,$ которые должны поддерживать заданную ценность взаимной информации с $Y\,$. Можно показать, что оптимум $T\,$ — нормальный вектор, состоящий из линейных комбинаций элементов $X,\,\,T=AX\,$ где матрица $A\,$ имеет ортогональные строки.

Матрица проекции $A\,$ на самом деле содержит $M\,$ строки, выбранные из взвешенных левых собственных векторов сингулярного разложения матрицы (обычно асимметричных)

$\Omega =\Sigma _{X|Y}\Sigma _{XX}^{-1}=I-\Sigma _{XY}\Sigma _{YY}^{-1}\Sigma _{XY}^{T}\Sigma _{XX}^{-1}.\,$

Определите разложение по сингулярным значениям

$\Omega =U\Lambda V^{T}{\text{ with }}\Lambda =\operatorname {Diag} {\big (}\lambda _{1}\leq \lambda _{2}\cdots \lambda _{N}{\big )}\,$

и критические значения

$\beta _{i}^{C}{\underset {\lambda _{i}<1}{=}}(1-\lambda _{i})^{-1}.\,$

тогда число $M\,$ активных собственных векторов в проекции или порядке приближения определяется выражением

$\beta _{M-1}^{C}<\beta \leq \beta _{M}^{C}$

И мы наконец получаем

$A=[w_{1}U_{1},\dots ,w_{M}U_{M}]^{T}$

В котором веса задаются выражением

$w_{i}={\sqrt {\left(\beta (1-\lambda _{i})-1\right)/\lambda _{i}r_{i}}}$

где $r_{i}=U_{i}^{T}\Sigma _{XX}U_{i}.\,$

Применение узкого места гауссовой информации к временным рядам (процессам) дает решения, связанные с оптимальным прогнозирующим кодированием. Эта процедура формально эквивалентна линейному анализу медленных функций.

Оптимальные временные структуры в линейных динамических системах могут быть обнаружены с помощью так называемого информационного узкого места прошлого будущего - применения метода узкого места к негауссовым выборочным данным. Эта концепция, как ее трактовали Крейциг, Тишби и др., не лишена сложностей, поскольку в этом упражнении есть два независимых этапа: во-первых, оценка неизвестных родительских плотностей вероятностей, из которых извлекаются выборки данных, и, во-вторых, использование этих плотностей в рамках теоретическая информационная основа узкого места.

Оценка плотности

Основная статья: Оценка плотности

Поскольку метод «узких мест» сформулирован в вероятностных, а не статистических терминах, основная плотность вероятности в точках выборки $X={x_{i}}\,$необходимо оценить. Это хорошо известная проблема с множеством решений, описанная Сильверманом . В настоящем методе вероятности совместной выборки находятся с использованием метода матрицы переходов Маркова , и это имеет некоторую математическую синергию с самим методом узкого места.

Произвольно возрастающая метрика расстояния $f\,$ между всеми парами выборок и расстояний матрицей $d_{i,j}=f{\Big (}{\Big |}x_{i}-x_{j}{\Big |}{\Big )}$ . Тогда вероятности перехода между парами выборок $P_{i,j}=\exp(-\lambda d_{i,j})\,$ для некоторых $\lambda >0\,$необходимо вычислить. Обработка выборок как состояний и нормализованной версии $P\,$ как матрица вероятности перехода марковского состояния, вектор вероятностей «состояний» после $t\,$ шаги, обусловленные исходным состоянием $p(0)\,$, является $p(t)=P^{t}p(0)\,$. Вектор равновесной вероятности $p(\infty )\,$ задается обычным образом доминирующим собственным вектором матрицы $P\,$ который не зависит от инициализирующего вектора $p(0)\,$. Этот метод перехода Маркова устанавливает вероятность в точках выборки, которая, как утверждается, пропорциональна плотности вероятностей там.

Другие интерпретации использования собственных значений матрицы расстояний $d\,$ обсуждаются в книге Сильвермана «Оценка плотности для статистики и анализа данных» .

Кластеры

В следующем примере мягкой кластеризации опорный вектор $Y\,$ содержит выборочные категории и совместную вероятность $p(X,Y)\,$ предполагается известным. Мягкий кластер $c_{k}\,$ определяется распределением вероятностей по выборкам данных $x_{i}:\,\,\,p(c_{k}|x_{i})$. Тишби и др. представлен следующий итерационный набор уравнений для определения кластеров, которые в конечном итоге являются обобщением алгоритма Блахута-Аримото , разработанного в теории искажений скорости . Применение этого типа алгоритма в нейронных сетях, по-видимому, связано с аргументами в пользу энтропии, возникающими при применении распределений Гиббса в детерминистическом отжиге.

${\begin{cases}p(c|x)=Kp(c)\exp {\Big (}-\beta \,D^{KL}{\Big [}p(y|x)\,||\,p(y|c){\Big ]}{\Big )}\\p(y|c)=\textstyle \sum _{x}p(y|x)p(c|x)p(x){\big /}p(c)\\p(c)=\textstyle \sum _{x}p(c|x)p(x)\\\end{cases}}$

Функция каждой строки итерации расширяется как

Строка 1: Это матричный набор условных вероятностей.

$A_{i,j}=p(c_{i}|x_{j})=Kp(c_{i})\exp {\Big (}-\beta \,D^{KL}{\Big [}p(y|x_{j})\,||\,p(y|c_{i}){\Big ]}{\Big )}$

Расхождение Кульбака – Лейблера $D^{KL}\,$ между $Y\,$ векторы, созданные на основе выборочных данных $x\,$ и те, которые генерируются его сокращенным информационным прокси $c\,$ применяется для оценки точности сжатого вектора по отношению к эталонным (или категориальным) данным. $Y\,$ в соответствии с фундаментальным уравнением узкого места. $D^{KL}(a||b)\,$ – это расхождение Кульбака – Лейблера между распределениями $a,b\,$

$D^{KL}(a||b)=\sum _{i}p(a_{i})\log {\Big (}{\frac {p(a_{i})}{p(b_{i})}}{\Big )}$

и $K\,$ является скалярной нормализацией. Взвешивание по отрицательному показателю расстояния означает, что вероятности предшествующих кластеров уменьшаются в строке 1, когда расхождение Кульбака – Лейблера велико, таким образом, вероятность успешных кластеров увеличивается, а неудачных - распада.

Строка 2: Второй матричный набор условных вероятностей. По определению

${\begin{aligned}p(y_{i}|c_{k})&=\sum _{j}p(y_{i}|x_{j})p(x_{j}|c_{k})\\&=\sum _{j}p(y_{i}|x_{j})p(x_{j},c_{k}){\big /}p(c_{k})\\&=\sum _{j}p(y_{i}|x_{j})p(c_{k}|x_{j})p(x_{j}){\big /}p(c_{k})\\\end{aligned}}$

где тождества Байеса $p(a,b)=p(a|b)p(b)=p(b|a)p(a)\,$ используются.

Строка 3: эта линия находит предельное распределение кластеров. $c\,$

${\begin{aligned}p(c_{i})&=\sum _{j}p(c_{i},x_{j})&=\sum _{j}p(c_{i}|x_{j})p(x_{j})\end{aligned}}$

Это стандартный результат.

Дополнительными входными данными для алгоритма являются предельное распределение выборки. $p(x)\,$ который уже определен доминирующим собственным вектором $P\,$ и матричная функция дивергенции Кульбака–Лейблера

$D_{i,j}^{KL}=D^{KL}{\Big [}p(y|x_{j})\,||\,p(y|c_{i}){\Big ]}{\Big )}$

полученные на основе интервалов между образцами и вероятностей перехода.

Матрица $p(y_{i}|c_{j})\,$ может быть инициализирован случайным образом или с разумным предположением, в то время как матрица $p(c_{i}|x_{j})\,$ не требует никаких предварительных значений. Хотя алгоритм сходится, может существовать несколько минимумов, которые необходимо будет разрешить.

Определение контуров решений

Чтобы классифицировать новый образец $x'\,$ внешний по отношению к обучающему набору $X\,$, предыдущая метрика расстояния находит вероятности перехода между $x'\,$ и все образцы в $X:\,\,$, ${\tilde {p}}(x_{i})=p(x_{i}|x')=\mathrm {K} \exp {\Big (}-\lambda f{\big (}{\Big |}x_{i}-x'{\Big |}{\big )}{\Big )}$ с $\mathrm {K} \,$ нормализация. Во-вторых, примените последние две строки трехстрочного алгоритма, чтобы получить вероятности кластера и условной категории.

${\begin{aligned}&{\tilde {p}}(c_{i})=p(c_{i}|x')=\sum _{j}p(c_{i}|x_{j})p(x_{j}|x')=\sum _{j}p(c_{i}|x_{j}){\tilde {p}}(x_{j})\\&p(y_{i}|c_{j})=\sum _{k}p(y_{i}|x_{k})p(c_{j}|x_{k})p(x_{k}|x')/p(c_{j}|x')=\sum _{k}p(y_{i}|x_{k})p(c_{j}|x_{k}){\tilde {p}}(x_{k})/{\tilde {p}}(c_{j})\\\end{aligned}}$

Окончательно

$p(y_{i}|x')=\sum _{j}p(y_{i}|c_{j})p(c_{j}|x'))=\sum _{j}p(y_{i}|c_{j}){\tilde {p}}(c_{j})\,$

Параметр $\beta \,$ должна находиться под пристальным наблюдением, поскольку по мере ее увеличения от нуля все большее число признаков в вероятностном пространстве категорий фокусируется на определенных критических порогах.

Пример

В следующем случае рассматривается кластеризация в четырехквадрантном множителе со случайными входными данными. $u,v\,$ и две категории продукции, $\pm 1\,$, созданный $y=\operatorname {sign} (uv)\,$. Эта функция имеет два пространственно разделенных кластера для каждой категории и, таким образом, демонстрирует, что метод может обрабатывать такие распределения.

Отбирают 20 проб, равномерно распределенных по площади. $[-1,1]^{2}\,$ . Количество используемых кластеров помимо количества категорий (в данном случае двух) мало влияет на производительность, и результаты отображаются для двух кластеров с использованием параметров. $\lambda =3,\,\beta =2.5$.

Функция расстояния $d_{i,j}={\Big |}x_{i}-x_{j}{\Big |}^{2}$ где $x_{i}=(u_{i},v_{i})^{T}\,$ в то время как условное распределение $p(y|x)\,$ представляет собой матрицу 2 × 20

${\begin{aligned}&Pr(y_{i}=1)=1{\text{ if }}\operatorname {sign} (u_{i}v_{i})=1\,\\&Pr(y_{i}=-1)=1{\text{ if }}\operatorname {sign} (u_{i}v_{i})=-1\,\end{aligned}}$

и ноль в другом месте.

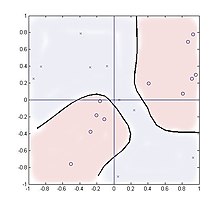
Суммирование в строке 2 включает только два значения, представляющие обучающие значения +1 или -1, но, тем не менее, работает хорошо. На рисунке показано расположение двадцати образцов, где «0» представляет Y = 1, а «x» представляет Y = -1. Показан контур на уровне отношения правдоподобия единицы:

$L={\frac {\Pr(1)}{\Pr(-1)}}=1$

как новый образец $x'\,$сканируется по площади. Теоретически контур должен совпадать с $u=0\,$ и $v=0\,$ координаты, но для такого малого количества выборок вместо этого они следовали ложным кластерам точек выборки.

Контуры решений

Аналогии с нейронными сетями и нечеткой логикой

Этот алгоритм чем-то похож на нейронную сеть с одним скрытым слоем. Внутренние узлы представлены кластерами $c_{j}\,$ а первый и второй слои весов сети — это условные вероятности $p(c_{j}|x_{i})\,$ и $p(y_{k}|c_{j})\,$ соответственно. Однако, в отличие от стандартной нейронной сети, алгоритм полностью полагается на вероятности в качестве входных данных, а не на сами выборочные значения, в то время как все внутренние и выходные значения представляют собой условные распределения плотности вероятности. Нелинейные функции инкапсулированы в метрике расстояния. $f(.)\,$ (или функции влияния/радиальные базисные функции ) и вероятности перехода вместо сигмовидных функций .

Трехстрочный алгоритм Блахута-Аримото сходится быстро, часто за десятки итераций, и при варьировании $\beta \,$, $\lambda \,$ и $f\,$ и мощности кластеров, можно достичь различных уровней внимания к функциям.

Определение статистической мягкой кластеризации $p(c_{i}|x_{j})\,$ имеет некоторое совпадение с концепцией вербального нечеткого членства нечеткой логики .

Расширения

Интересным расширением является случай информационного узкого места с дополнительной информацией. Здесь информация максимизируется об одной целевой переменной и минимизируется о другой, создавая представление, которое информативно об выбранных аспектах данных. Формально

$\min _{p(t|x)}\,\,I(X;T)-\beta ^{+}I(T;Y^{+})+\beta ^{-}I(T;Y^{-})$

Библиография

• Вайс, Ю. (1999), «Сегментация с использованием собственных векторов: объединяющий взгляд», Труды Международной конференции IEEE по компьютерному зрению (PDF) , стр. 975–982.
• П. Харремос и Н. Тишби «Возвращение к узкому месту в информации или как выбрать хороший показатель искажения». В материалах Международного симпозиума по теории информации (ISIT) 2007 г.