Моноидальный функтор
В теории категорий моноидальные функторы — это функторы между моноидальными категориями , которые сохраняют моноидальную структуру. Более конкретно, моноидальный функтор между двумя моноидальными категориями состоит из функтора между категориями, а также двух карт когерентности — естественного преобразования и морфизма, которые сохраняют моноидальное умножение и единицу соответственно. Математики требуют, чтобы эти карты когерентности удовлетворяли дополнительным свойствам в зависимости от того, насколько строго они хотят сохранить моноидальную структуру; каждое из этих свойств приводит к несколько иному определению моноидальных функторов.
- Отображения когерентности нестрогих моноидальных функторов не обладают никакими дополнительными свойствами; они не обязательно обратимы.
- Отображения когерентности сильных моноидальных функторов обратимы.
- Отображения когерентности строгих моноидальных функторов являются тождественными.
Хотя здесь мы различаем эти разные определения, авторы могут называть любое из этих просто моноидальных функторов .
Определение [ править ]
Позволять и быть моноидальными категориями. Слабый моноидальный функтор из к (который также можно назвать моноидальным функтором) состоит из функтора вместе с естественным преобразованием
между функторами и морфизм
- ,
называемые картами когерентности или структурными морфизмами , которые таковы, что для каждых трех объектов , и из диаграммы
ездить в категории . Выше различные естественные преобразования, обозначенные с помощью являются частями моноидальной структуры на и .
Варианты [ править ]
- Двойственным моноидальному функтору является комоноидальный функтор ; это моноидальный функтор, карты когерентности которого перевернуты. Комоноидальные функторы также можно назвать опмоноидальными, моноидальными функторами колакса или моноидальными функторами оплакса.
- Сильный моноидальный функтор — это моноидальный функтор, когерентность которого отображается являются обратимыми.
- Строгий моноидальный функтор — это моноидальный функтор, карты когерентности которого являются тождествами.
- Скрученный моноидальный функтор — это моноидальный функтор между сплетенными моноидальными категориями (расплетения обозначаются ) такая, что следующая диаграмма коммутирует для каждой пары объектов A , B в :
- Симметричный моноидальный функтор — это плетеный моноидальный функтор, область определения и кодомен которого являются симметричными моноидальными категориями .
Примеры [ править ]
- Базовый функтор из категории абелевых групп в категорию множеств. В этом случае карта отправляет (a, b) в ; карта отправляет до 1.
- Если является (коммутативным) кольцом, то свободный функтор продолжается до сильно моноидального функтора (а также если коммутативен).
- Если является гомоморфизмом коммутативных колец, то функтор ограничения является моноидальным, а функтор индукции является сильно моноидальным.
- Важным примером симметричного моноидального функтора является математическая модель топологической квантовой теории поля недавно разработанная . Позволять — категория кобордизмов n -1,n -мерных многообразий с тензорным произведением, заданным дизъюнктным объединением, и за единицу — пустое многообразие. Топологическая квантовая теория поля в размерности n представляет собой симметричный моноидальный функтор.
- Функтор гомологии моноидален как через карту .
Альтернативные понятия [ править ]
Если и являются замкнутыми моноидальными категориями с внутренними hom-функторами (нижние индексы опустим для удобства чтения), есть альтернативная формулировка
- ψ AB : F ( А ⇒ B ) → FA ⇒ FB
φ функциональном AB обычно используется в программировании . Связь между ψ AB и φ AB иллюстрируется следующими коммутативными диаграммами:
Свойства [ править ]
- Если является моноидным объектом в , затем является моноидным объектом в .
и Моноидальные дополнения функторы
Предположим, что функтор остается сопряженным слева с моноидом . Затем имеет комоноидальное строение вызванный , определяемый
и
- .
Если индуцированная структура на является сильным, то единица и единица присоединения являются моноидальными естественными преобразованиями , и присоединение называется моноидальным присоединением ; и наоборот, левый сопряженный моноидального присоединения всегда является сильным моноидальным функтором.
Аналогично, правый сопряженный комоноидальному функтору является моноидальным, а правый сопряженный комоноидальному присоединению является сильным моноидальным функтором.
См. также [ править ]
Ссылки [ править ]
- Келли, Дж. Макс (1974). «Доктринальное дополнение». Категория Семинар . Конспект лекций по математике. Том. 420. Спрингер. стр. 257–280. дои : 10.1007/BFb0063105 . ISBN 978-3-540-37270-7 .











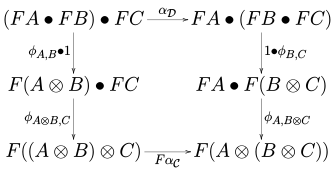





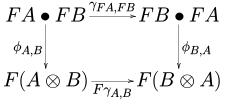














![{\ displaystyle (Ch (R {\ mathsf {-mod}}), \ otimes, R [0]) \ to (grR {\ mathsf {-mod}}, \ otimes, R [0])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b5b3f3ab1c1e64cb4bc1848cedd0ae03b5e833f)
![{\displaystyle H_{\ast }(C_{1})\otimes H_{\ast }(C_{2})\to H_{\ast }(C_{1}\otimes C_{2}),[x_{ 1}]\otimes [x_{2}]\mapsto [x_{1}\otimes x_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88c1233008efff53b6dd10c40d0c790e60440b6c)











