Наклонное поле

Поле наклона (также называемое полем направления) ^[1]) — графическое представление решений дифференциального уравнения первого порядка ^[2] скалярной функции. Решениями поля наклонов являются функции, изображенные в виде сплошных кривых. Поле наклона показывает наклон дифференциального уравнения на определенных интервалах по вертикали и горизонтали на плоскости xy и может использоваться для определения приблизительного наклона касательной в точке кривой, где кривая является некоторым решением дифференциального уравнения.

Определение

Стандартный корпус

Поле наклона может быть определено для дифференциальных уравнений следующего типа:

y'=f(x,y),

что можно геометрически интерпретировать как наклон к графику касательной решения дифференциального уравнения ( интегральной кривой ) в каждой точке ( x , y ) как функцию координат точки. ^[3]

Его можно рассматривать как творческий способ построения действительной функции двух действительных переменных. $f(x,y)$ как плоская картина. В частности, для данной пары $x,y$ , вектор с компонентами $[1,f(x,y)]$ рисуется в точке $x,y$ на $x,y$ -самолет. Иногда вектор $[1,f(x,y)]$ нормализуется, чтобы график лучше смотрелся человеческим глазом. Набор пар $x,y$ Для рисования обычно используется прямоугольная сетка.

Изоклина . (серия линий с одинаковым наклоном) часто используется для дополнения поля уклонов В уравнении вида $y'=f(x,y)$ , изоклина – это линия, $x,y$ -плоскость, полученная установкой $f(x,y)$ равна константе.

Общий случай системы дифференциальных уравнений

Учитывая систему дифференциальных уравнений,

{\begin{aligned}{\frac {dx_{1}}{dt}}&=f_{1}(t,x_{1},x_{2},\ldots ,x_{n})\\{\frac {dx_{2}}{dt}}&=f_{2}(t,x_{1},x_{2},\ldots ,x_{n})\\&\;\;\vdots \\{\frac {dx_{n}}{dt}}&=f_{n}(t,x_{1},x_{2},\ldots ,x_{n})\end{aligned}}

поле наклона представляет собой массив меток наклона в фазовом пространстве (в любом количестве измерений в зависимости от количества соответствующих переменных; например, двух в случае линейного ОДУ первого порядка , как показано справа). Каждая отметка уклона центрируется в точке $(t,x_{1},x_{2},\ldots ,x_{n})$ и параллелен вектору

{\begin{pmatrix}1\\f_{1}(t,x_{1},x_{2},\ldots ,x_{n})\\f_{2}(t,x_{1},x_{2},\ldots ,x_{n})\\\vdots \\f_{n}(t,x_{1},x_{2},\ldots ,x_{n})\end{pmatrix}}.

Количество, положение и длина отметок уклона могут быть произвольными. Позиции обычно выбираются так, чтобы точки $(t,x_{1},x_{2},\ldots ,x_{n})$ сделать равномерную сетку. Стандартный случай, описанный выше, представляет собой $n=1$ . Общий случай поля наклонов для систем дифференциальных уравнений нелегко визуализировать для $n>2$ .

Общее применение

С помощью компьютеров можно быстро и без утомления создать сложные поля уклонов, и поэтому лишь в последнее время их практическое применение заключается в том, чтобы использовать их просто для того, чтобы почувствовать, каким должно быть решение, прежде чем искать явное общее решение. Конечно, компьютеры также могут решить одну задачу, если она существует.

Если нет явного общего решения, компьютеры могут использовать поля наклона (даже если они не показаны) для численного поиска графических решений. Примерами таких процедур являются метод Эйлера или, лучше сказать, методы Рунге-Кутты .

Программное обеспечение для построения полей уклонов

Различные пакеты программного обеспечения могут отображать поля уклонов.

Код поля направления в GNU Octave / MATLAB

funn = @(x, y)y-x;                             % function f(x, y) = y-x
[x, y] = meshgrid(-5:0.5:5);                   % intervals for x and y
slopes = funn(x, y);                           % matrix of slope values
dy = slopes ./ sqrt(1 + slopes.^2);            % normalize the line element...
dx = ones(length(dy)) ./ sqrt(1 + slopes.^2);  % ...magnitudes for dy and dx
h = quiver(x, y, dx, dy, 0.5);                 % plot the direction field
set(h, "maxheadsize", 0.1);                    % alter head size

Пример кода для Максимы

/* field for y'=xy (click on a point to get an integral curve). Plotdf requires Xmaxima  */
plotdf( x*y, [x,-2,2], [y,-2,2]);

Пример кода для Mathematica

(* field for y'=xy *)
VectorPlot[{1,x*y-5x},{x,-2,2},{y,-2,2}]

Пример кода для SageMath ^[4]

var('x,y')
plot_slope_field(x*y, (x,-2,2), (y,-2,2))

Примеры

у' = х/у
Наклонное поле
Интегральные кривые
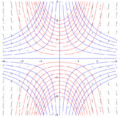
Изоклины (синие), поле уклонов (черные) и некоторые кривые решения (красные).

См. также

Ссылки

^ Бойс, Уильям (2001). Элементарные дифференциальные уравнения и краевые задачи (7-е изд.). Уайли. п. 3. ISBN 9780471319993 .
^ Владимир Александрович Добрушкин (2014). Прикладные дифференциальные уравнения: начальный курс . ЦРК Пресс. п. 13. ISBN 978-1-4987-2835-5 .
^ Андрей Дмитриевич Полянин; Александр В. Манжиров (2006). Справочник по математике для инженеров и ученых . ЦРК Пресс. п. 453. ИСБН 978-1-58488-502-3 .
^ «Отображение полей — Справочное руководство Sage 9.4: 2D-графика» .

Бланшар, Пол; Девани, Роберт Л .; и Холл, Глен Р. (2002). Дифференциальные уравнения (2-е изд.). Брукс/Коул: Обучение Томпсона. ISBN 0-534-38514-1

Внешние ссылки

[1] Бойс, Уильям (2001). Элементарные дифференциальные уравнения и краевые задачи (7-е изд.). Уайли. п. 3. ISBN 9780471319993 .

[2] Владимир Александрович Добрушкин (2014). Прикладные дифференциальные уравнения: начальный курс . ЦРК Пресс. п. 13. ISBN 978-1-4987-2835-5 .

[3] Андрей Дмитриевич Полянин; Александр В. Манжиров (2006). Справочник по математике для инженеров и ученых . ЦРК Пресс. п. 453. ИСБН 978-1-58488-502-3 .

[4] «Отображение полей — Справочное руководство Sage 9.4: 2D-графика» .

[1]

[2]

[3]

[4]